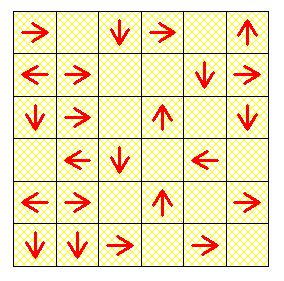
|
#1 - 23-05-2020 09:34:44
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
#2 - 23-05-2020 12:11:37
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3839
Echhecs 24
Salut Vasimolo. Qu'appelles tu " vider la grille " ? Un robot peut sortir s'il n'est pas empêché par un autre dans son sens de déplacement ?
#3 - 23-05-2020 12:28:28
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
EEchecs 24
Oui , ce n'était pas clair ?
Vasimolo
#4 - 23-05-2020 12:48:08
- Migou
- Expert de Prise2Tete
- Enigmes résolues : 17
- Messages : 893
- Lieu: Ville 2/N près 2*i
ecjecs 24
Bonjour Vasimolo.
Ma réponse : pour toute position, les robots peuvent sortir.
démonstration
Si j'ai bien compris, les robots s'arrêtent toujours à la première flèche rencontrée (ou alors ils sortent de la grille)
Au premier tour, les robots ne sont pas nécessairement sur une flèche. au second tour, soit le robot en suivant la direction vers laquelle il pointe sort, soit il se retrouve sur une flèche.
Partons donc sans perdre de généralité* d'une position où tous les robots sont sur une flèche.
Lemme (que je ne démontre pas)))) Dans ce cas, la seule façon de rendre la sortie impossible serait d'avoir un cycle (un parcours de flèches se refermant sur lui même).
Or dans la configuration actuelle, en testant chaque flèche de départ potentielle, on finit toujours à l'extérieur.
Conclusion il n'existe pas de cycle de flèches dans cette grille.
Conclusion (grâce au lemme) : la sortie des robots est toujours possible dans cette grille.
*Pour être sûr de pouvoir atteindre l'étape 2, il est nécessaire qu'aucun robot ne point vers un autre robot. Si on relâchait la condition (3) en autorisant par exemple qu'un robot pointe vers un autre robot pour peu que cet autre robot pointe ailleurs, on pourrait produire un "gridlock"
|--|--|
| v|<|
|--|--|
| >|^|
|--|--|
#5 - 23-05-2020 16:32:42
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3839
echzcs 24
OK.
Et pourquoi le code de la route interdit-il de s'engager sur un carrefour à priorité à droite quand on ne peut pas le dégager ?
#6 - 23-05-2020 17:40:58
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
Ecchecs 24
@Migou
L'illustration , n'était sans doute pas assez claire , les flèches sont portées par les robots . Il ne peut pas y avoir de cycle , c'est en effet assez évident mais jamais de blocages , pourquoi ?
Vasimolo
#7 - 23-05-2020 19:18:37
- caduk
- Professionnel de Prise2Tete
- Enigmes résolues : 45
- Messages : 398
Echecs 42
Au début, on choisit un robot que l'on fait avancer au maximum. S'il sort, tant mieux et on en choisit un autre. S'il finit par pointer un autre robot, alors on choisit le robot qu'il pointe pour le bouger, et ainsi de suite. On n'aura jamais plus de un robot qui en pointe un autre car quand ça arrive, on dégage le robot de devant, qui en pointera alors au plus un autre. il n'y a clairement pas de cycle, les robots ne pouvant faire qu'avancer dans leur direction. Il finiront donc tous par sortir.
Merci pour cette énigme 
#8 - 23-05-2020 19:25:20
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
echecd 24
@Caduk
Ce n'est pas aussi simple , chaque robot n'a pas forcément une case libre en face de lui .
Vasimolo
#9 - 23-05-2020 19:39:43
- caduk
- Professionnel de Prise2Tete
- Enigmes résolues : 45
- Messages : 398
echevs 24
Pourtant, tu as marqué qu'initialement, si. Dans ce cas, mon procédé garde le nombre de robots en pointant un autre plus petit que 1. On aura donc toujours des robots ayant une case libre devant eux...
Si ce n'est pas le cas à l'instant initial, alors c'est très facile de trouver des contres exemples...
En relisant ma solution, je me rends compte qu'elle n'était effectivement pas si claire, je l'ai modifiée 
Edit : A mince, il peut se mettre devant un robot, ce qui augmente le compte de deux, on doit pouvoir contourner ça...
#10 - 24-05-2020 07:57:57
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3839
Ehecs 24
>>>>>>>>>>>V
^......................V
^......................V
^......................V
^......................V
^......................V
^......................V
^<<<<<<<<<<<
Blocage !
#11 - 24-05-2020 08:33:39
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
echrcs 24
@Nodgim : ton exemple n'est pas bon , chaque robot doit initialement pointer vers une case vide .
Vasimolo
#12 - 24-05-2020 12:51:24
- TOUFAU
- Professionnel de Prise2Tete
- Enigmes résolues : 0
- Messages : 105
Echecs 4
Pas sur de comprendre : chaque robot a une direction immuable? à chaque 'tour', tout robot qui peut bouger avance d'une case? si deux robots pointent sur une même case vide, que se passe t-il au tour suivant?
Mon interprétation n'est sans doute pas bonne car elle conduit à un cas de blocage trivial (ex: 4 robots sur un damier 2x2, chacun pointant dans le sens des aiguilles d'une montre par rapport au centre du damier)
#13 - 24-05-2020 16:09:15
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
echexs 24
La direction est bien immuable et à chaque coup on déplace un unique robot vers la case voisine vide désignée par la flèche . Un robot au bord de la grille et pointant vers l'extérieur peut sortir au coup suivant . J'espère que c'est plus clair .
Vasimolo
#14 - 24-05-2020 18:09:24
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3839
Echces 24
Bon, ce qu'il faut voir c'est qu'on peut attribuer un sens unique pour chaque ligne et chaque colonne.
Comme, dans le sens de déplacement, initialement, il y a toujours 1 case libre en aval de chaque flèche, alors on peut libérer d'abord par exemple toutes les lignes horizontales impaires, en déplaçant les flèches verticales gênantes et en sortant les flèches horizontales. Ensuite, du fait qu'on vient de libérer toutes les cases des lignes impaires, on peut y placer toutes les flèches verticales. On libère alors les lignes paires en sortant les flèches horizontales. Il ne reste plus alors de flèches horizontales, on peut sortir toutes les flèches verticales.
#15 - 24-05-2020 18:38:24
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
Echesc 24
Oui Nodgim , tu as vu l'astuce 
Alors , simple ou pas simple ?
Vasimolo
#16 - 24-05-2020 19:57:06
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3839
Echesc 24
Assez simple finalement. La simplicité réside, à mon sens, dans le nombre d'essais d'idées qu'on va y consacrer.
Essais ayant échoué :
- Suivre un trajet de flèches en supposant qu'on aura toujours une issue.
- Attribuer un nombre à chaque flèche égal au nombre des autres flèches perpendiculaires gênant la sortie, en espérant trouver une somme totale strictement décroissante à chaque mouvement.
- Prouver qu'on peut faire sortir les flèches des lignes ou colonnes périphériques, puis récurrence. Ce dernier essai préfigure la solution.
#17 - 24-05-2020 22:36:24
- Migou
- Expert de Prise2Tete
- Enigmes résolues : 17
- Messages : 893
- Lieu: Ville 2/N près 2*i
Echesc 24
Eh bien,
C'est pas si évident que ça. On sent qu'il est impossible d'atteindre un blocage.
Mais comment le justifier ?
#18 - 24-05-2020 22:40:32
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
rchecs 24
D'après Nodgim , c'est assez simple . Pour moi ça ne l'est pas , même si c'est limpide quand on voit la solution ( très courte ) .
Vasimolo
#19 - 25-05-2020 07:53:50
- Migou
- Expert de Prise2Tete
- Enigmes résolues : 17
- Messages : 893
- Lieu: Ville 2/N près 2*i
Eches 24
Une petite question sur le mouvement des robots : est-on d'accord qu'il s'agit de robots avec une intelligence collective qui choisissent toujours la meilleure strategie commune pour eviter les blocages ?
#20 - 25-05-2020 12:35:59
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
echecd 24
Bien sûr , on cherche une stratégie pour l'ensemble des robots .
Vasimolo
#21 - 25-05-2020 14:18:22
- Ebichu
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 888
cEhecs 24
Salut Vasimolo,
voici une stratégie qui m'a l'air de fonctionner.
1/ On amène tous les robots horizontaux sur une colonne d'indice pair, en les déplaçant de 0 ou 1 case.
2/ On éjecte tous les robots verticaux qui sont sur les colonnes d'indice impair. Ces colonnes sont ensuite vides.
3/ On amène tous les robots horizontaux sur une colonne d'indice impair, en les déplaçant de 1 case. C'est possible car ces colonnes sont vides.
4/ On éjecte les robots verticaux restant, puis les robots horizontaux.
Niveau de difficulté : je te hais.
#22 - 25-05-2020 19:46:00
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
ecgecs 24
Oui , c'est ça Ebichu 
Trop simple !
Vasimolo
Et comme il ne faut pas résister aux plaisirs simples , j'ai rajouté un peu de temps .
#23 - 29-05-2020 00:02:16
- caduk
- Professionnel de Prise2Tete
- Enigmes résolues : 45
- Messages : 398
Echces 24
Bon, je réessaye.
On choisit un robot. Dès qu'il heurte un autre robot, on bouge ce robot (jusqu'à ce qu'il en heurte en autre, etc, etc...
Si le robot déplacé sort, on recommence avec un autre.
Si le robot heurté est déjà heurté à un autre, on prend le suivant.
On construit un graphe orienté en associant chaque robot au premier devant lui (si il y en a un). On appelle boucle de robots un boucle dans ce graphe. La boucle est dite fermée si tout les robots de la boucle sont collés au robot de devant. Une configuration devient impossible si et seulement si elle aboutit à une boucle fermée.
Le procédé décrit ne permet pas de créer de boucles fermées.
En effet, si un robot, en en heurtant un autre, crée une quasi boucle (boucle fermée ou l'on retire un robot dans l'un des angles de la boucle), alors la propagation dans la boucle va faire avancer le robot du coin et casser la quasi boucle. (et si se déplacement crée un quasi boucle, on répète le même argument).
Pour qu'un robot, en en heurtant un autre, crée une boucle fermée, il faut que le robot qu'il heurte fasse partie d'une quasi boucle (c'est la seule possibilité, on le voit en partant d'une boucle fermée et en "rembobinant" : on ne peut que faire reculer un robot dans un coin, créant ainsi une quasi boucle).
Or les quasi boucles créées étant immédiatement détruites, ce scénario ne peut arriver.
C'est assez simple, mais pas si évident à trouver (je suis sans doute passé à côté d'une preuve beaucoup plus simple...)
#24 - 29-05-2020 11:35:28
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
Ececs 24
@Caduk : ça marche peut-être mais c'est hyper difficile à suivre avec des boucles dans les boucles , dans les boucles ...
Il y a une solution très simple à comprendre et à réaliser .
Je donne un indice dans le message initial .
Tu vas tout de suite comprendre 
Vasimolo
#25 - 29-05-2020 12:34:07
- caduk
- Professionnel de Prise2Tete
- Enigmes résolues : 45
- Messages : 398
Echeecs 24
Ma démonstration n'est pas si compliquée en vrai.
Effectivement, on peut amener les robots qui se déplacent vers le haut ou le bas sur les lignes paires, vider les lignes impaires, amener ces mêmes robots sur les lignes impaires, vider les lignes impaires, puis finir de vider la grille. J'avais pensé à ce genre de technique, je ne sais pas pourquoi je n'ai pas réussi à l'aboutir.
Néanmoins, je pense que ma méthode est beaucoup plus générale, puisque elle permet de gérer de très nombreux cas ou des robots sont collés aux autres, et je pense que je ne suis pas loin de la condition nécessaire et suffisante pour vider la grille.  à voir... à voir...
|
 |

 Accueil
Accueil
 Forum
Forum