 |
#1 - 10-03-2013 10:39:16
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3839
Manège d'entiers rleatifs
Bonjour à tous.
On dispose 100 nombres entiers relatifs en cercle. Vous ne pouvez en observer que 5 à la fois, à travers un secteur angulaire de 10 nombres avec seulement 5 ouvertures. Vous pouvez placer votre secteur angulaire où vous voulez sur le cercle. Vous avez à votre disposition certains secteurs angulaires, qu'on peut modéliser par un code binaire à 10 chiffres dont les 1 sont les ouvertures qui permettent de voir les nombres.
Vous pouvez agir sur le signe + ou - des nombres observables à votre guise, mais si vous décidez de changer le signe des 5 nombres, ils changent tous de signe en même temps.
Question: pourrez vous obtenir, au bout d'un certain nombre de changements de signe, une configuration telle que, quel que soit le secteur angulaire que vous utiliserez, et à quelque emplacement que vous le positionnerez, vous aurez toujours une somme des 5 nombres observables positive ou nulle ?
Bon amusement
#2 - 10-03-2013 12:27:32
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 6,191E+3
Manèg d'entiers relatifs
Je n'ai pas du bien comprendre l'énoncé car ça me parait assez trivial :
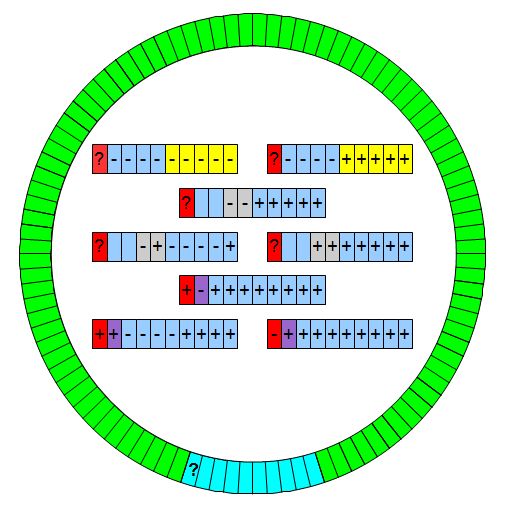
1) on repère (en rouge) le plus petit nombre en valeur absolue.
2 ) en décalant un cache on met tous les nombres à l'état positif (vert) sauf les 10 autour du rouge.
3) on peut facilement obtenir au moins 5 + (jaune)
4) si il y a 2 - on peut les rendre + (gris)
5 ) si il reste un - :
soit le rouge était - et on change les deux en +
Soit le rouge était + et on intervertit les deux signes (mauve)
Il ne reste qu'un nombre négatif dans le cercle , le plus petit en valeur absolue.
Si on ne peut pas repasser sur un même nombre avec plusieurs caches, c'est impossible dans lae cas , par exemple où ils sont tous négatifs dès le début.
#3 - 10-03-2013 13:34:50
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3839
manège d'entierd relatifs
Oui Gwen.
Suppose maintenant que tu ne disposes que d'un seul secteur à configuration imposée, répondras tu la même chose ?
Par exemple
0101010011
#4 - 10-03-2013 14:05:42
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 6,191E+3
Manège d'entiers relatfis
0101010011
Bah oui, il y a 5 zéros, je les change tous les 5.
1111111111
Ou alors tu parles du cache ?
OK, je ne sais pas encore ...
#5 - 10-03-2013 16:27:27
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3839
mznège d'entiers relatifs
Suite à une remarque de Gwen, j'ai apporté une petite modification de l'énoncé (on vous donne certains secteurs angulaires, et non tous) sinon c'est trop facile.
Bonne réflexion.
#6 - 10-03-2013 17:11:56
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 6,191E+3
manège d'entiers rrlatifs
Avec 2 secteurs angulaires, c'est simple aussi, je prends ces deux là :
1111010000
1111100000
Si le second chiffre en gras est positif, je ne touche à rien et je décale le cache.
Si le second est négatif, j'applique les deux caches puis je décale d'un cran.
Avec un seul, c'est plus difficile et je ne trouve pas de solution.
#7 - 10-03-2013 19:38:52
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3839
manège d'entiers relayifs
Gwen, les secteurs te sont imposés, ce n'est pas toi qui les choisis.
#8 - 11-03-2013 07:23:31
- golgot59
- Elite de Prise2Tete
- Enigmes résolues : 48
- Messages : 1494
- Lieu: Coutiches
Manège d'entiers reltifs
J'ai du mal à comprendre l'énoncé qui me parait intéressant pourtant :
Vous pouvez placer votre secteur angulaire où vous voulez sur le cercle.
et :
Gwen, les secteurs te sont imposés, ce n'est pas toi qui les choisis.
#9 - 11-03-2013 18:31:13
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3839
manège d'entiers relatifd
Pour répondre à Golgot: les secteurs angulaires qu'on met à votre disposition, vous pouvez les placer à votre guise: du 1er au 10 ème nombre, du 35ème au 44éme nombre, du 95ème au 4ème, etc...
On met à votre disposition quelques secteurs angulaires, dont le code est quelconque, c'est à vous de débrouiller après de les utiliser au mieux.
Ou, encore mieux, de réfléchir un bon moment avant de vous en servir....
#10 - 11-03-2013 21:55:41
- golgot59
- Elite de Prise2Tete
- Enigmes résolues : 48
- Messages : 1494
- Lieu: Coutiches
Mangèe d'entiers relatifs
OK, c'est le nom qui me posait problème !
En fait, tu nous donnes des "filtres" qui parcourent 10 nombres consécutifs des 100 nombres disponibles mais avec 1 code qui ne laissent visibles que 5 nombres parmi les 10.
On peut placer ces "filtres" où on veut sur le cercle. C'est bien ça ?
Si c'est le cas, on peut parcourir le cercle complet en déplaçant le même filtre 1 nombre après l'autre et ainsi connaître tous les nombres sur le cercle, non ?
Et question supplémentaire : lorsqu'on change le signe d'un chiffre, ce sont bien les 5 observés et non les 10 sous le filtre qui changent de signe, c'est bien ça ?
#11 - 12-03-2013 16:03:48
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3839
manège d'entuers relatifs
#12 - 14-03-2013 18:25:49
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3839
manèhe d'entiers relatifs
Ce problème ne suscite pas, loin s'en faut, une passion démesurée.
Je vais donner un indice qui va peut être éveiller des vocations: La réponse est courte, elle tient sur une ligne !
Indice 2: chercher une convergence, qu'on peut aussi définir comme un invariant.
C'est beaucoup plus facile qu'il n'y parait....
#13 - 14-03-2013 19:41:45
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
manège d'entiers telatifs
A priori le problème m’intéresserait si j'arrivais à comprendre la question 
Vasimolo
#14 - 15-03-2013 18:00:40
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3839
manège d'entierq relatifs
Qu'est ce que tu ne comprends pas Vasimolo ?
#15 - 15-03-2013 19:11:02
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
Manège d'entierrs relatifs
Bonsoir Nodgim
Je vais plutôt te dire ce que j'ai cru comprendre .
Tu découpes un disque en 100 secteurs circulaires de même taille=1 et tu écris un nombre dans chaque secteur . Ensuite tu disposes d'un certain nombre de secteurs ( caches ) de taille 10 qui tous ont 5 secteurs transparents et 5 secteurs opaques . Tu peux poser ton cache n'importe où puis , au choix , changer le signe de tous les nombres qui apparaissent ou ne rien changer du tout . Tu recommences autant que tu veux avec tous les caches que tu veux , l'objectif final étant que quelque soit le cache choisi et quelque soit sa position , la somme des cinq nombres apparaissant par transparence soit positive ou nulle .
Après quelle est la question ? Faut-il caractériser la collection de caches pour lesquels on peut toujours atteindre l'objectif quelque soient les 100 nombres initialement choisis ?
Vasimolo
#16 - 15-03-2013 20:10:50
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3839
manège d'entiers relatigs
Je vois que c'est compris. La question est pourtant claire: on donne un certain nombre de secteurs, pourras tu toujours, quel que soit le nombre de secteurs qu'on te donne, et quel que soit leur code, parvenir au résultat demandé ? A savoir, avec les secteurs qu'on t'a donnés, et avec la possiblité que tu as de changer le signe des sommes des 5 nombres visibles, arriver à n'avoir que des sommes positives ou nulles, sommes obtenues avec les secteurs qu'on t'a donnés ?
La réponse est oui. Mais pourquoi ?
#17 - 16-03-2013 07:35:43
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
manègr d'entiers relatifs
Le plus difficile est en effet de comprendre la question 
On considère l'ensemble des résultats que l'on peut obtenir en plaçant les caches et en inversant les signes . Le nombre de résultats est fini , on peut donc considérer l'un de ceux qui réalisent une somme maximale . Si pour ce résultat l'un des caches laissait apparaître une somme négative il suffirait de changer les signes des 5 nombres apparaissant sous le cache pour dépasser le maximum .
Vasimolo
#18 - 16-03-2013 08:04:37
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3839
manège d'entizrs relatifs
C'est bien ça. La somme algébrique des cent nombres, quand on transforme de négative en positive une somme de 5 nombres, crôit strictement. Or, cette somme algébrique est majorée au pire par la somme de la valeur absolue des cent nombres.
C'est une libre reprise d'un problème d'Olympiade, qui mettait n*m nombres dans un rectangle, et sur lequel on pouvait agir sur le signe de la somme d'une ligne ou d'une colonne.
#19 - 16-03-2013 10:09:07
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
Manège d'ntiers relatifs
Cet exercice m'en rappelle un autre beaucoup plus subtil .
On dispose d'un quadrillage illimité dans tous les sens et deux caches quelconques que l'on peut placer où l'on veut sur le quadrillage ( en effectuant des translations suivant les carreaux ) . Chaque case du quadrillage contient un nombre réel et les caches laissent apparaître certaines cases par transparence comme dans le problème de Nodgim
On sait aussi que si on place le premier cache n'importe où , la somme des nombres apparaissant par transparence est toujours positive .
Montrer qu'il existe une place pour le deuxième cache laissant aussi apparaître un total positif .
Vasimolo
#20 - 16-03-2013 11:20:08
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 6,191E+3
Manège d'enters relatifs
Bizarrement, ton exemple plus subtil me parait beaucoup plus simple. Il suffit de dessiner un cache avec les déplacements du second.
#21 - 16-03-2013 11:36:26
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
Manège d'entiers relatis
Je ne vois pas ce que tu veux dire Gwen , les deux caches n'ont bien sûr pas la même forme .
Vasimolo
#22 - 16-03-2013 11:44:30
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 6,191E+3
Manège d'enttiers relatifs
J'ai bien compris. MP envoyé.
#23 - 16-03-2013 12:22:31
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
#24 - 16-03-2013 13:20:17
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3839
MManège d'entiers relatifs
Je le vois comme ça:
On observe 1 seule ligne. Le 1er cache s'y déplace d'une case à la fois. Si le 1er cache comporte k fenêtres, au bout d'un certain nombre de déplacements, on peut dire que la somme totale observée, pour tous les déplacements, vaut k fois chacun des nombres de la ligne. Cette somme est évidemment positive.
On fait la même chose avec le second cache sur les mêmes cases, au bout d'un certain nombre de déplacements, la somme totale vaudra environ j fois les mêmes nombres que le 1er cache. j fois cette somme sera aussi positif, puisque k fois l'est.
Or on ne peut avoir du positif avec uniquement des sommes partielles toutes négatives.
#25 - 16-03-2013 14:16:16
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 6,191E+3
Manège d'entierss relatifs
OK, je ne développe pas ici, mais c'est un sujet qui serait intéressant à proposer avec des réponses cachées car il est différent , à mon avis, de celui proposé par nodgim. 
Mots clés des moteurs de recherche
|
 |

 Accueil
Accueil
 Forum
Forum






