En posant b=r/(1-r), je trouve :

HG=[b(b²+1)-2b²]/(1-b²)

Voici un aperçu de ma recherche :



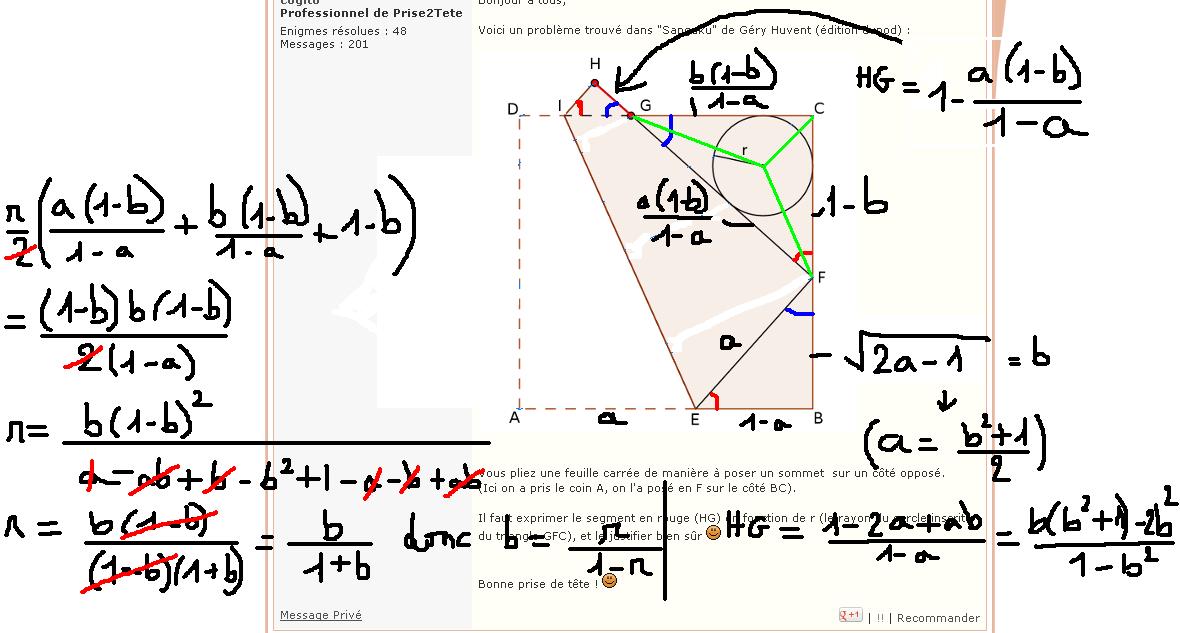
Pour faire vite, j'ai commencé par définir le carré de côté 1, et la distance AE=a

J'en ai déduit EF, EB et par Pythagore BF que j'ai nommé b, puis par triangles BEF et FGC semblables (angles égaux) de rapport (1-b)/(1-a) les longueurs des côtés du triangle FGC, et enfin la longueur HG.

Ensuite j'ai calculé l'aire de FGC de 2 façons différentes (directement et par la somme des 3 triangles de sommet le centre du cercle), j'ai ainsi obtenu b en fonction de r

Ensuite il n'y a plus eu qu'à remplacer.

J'ai fait ces calculs un peu vite, on est dimanche matin, je ne suis pas à l'abris d'une ou 2 coquilles...

Proposition

J'ai sauvé ma soirée en résolvant ce problème, ce aurait été dommage de ne pas y arriver après avoir annulé une sortie pour ...

Je reprends la figure


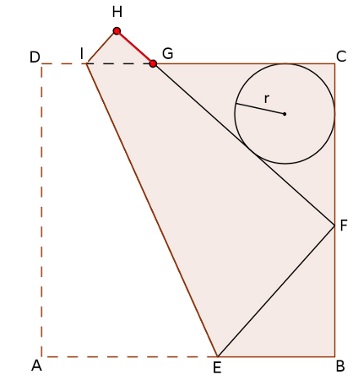
Notons x=AE.
Supposons AB=BC=BD=AD=1.
Notons enfin par [latex](A,\vec{i},\vec{j})[/latex], un repère orthonormé direct de centre A tel que [latex]\vec{i}=\overrightarrow{AB}[/latex] et [latex]\vec{j}=\overrightarrow{AD}[/latex].

EF=AE=x,
[TeX]EF^2=EB^2+BF^2[/latex] donc [latex]BF^2=x^2-(1-x)^2[/latex] d'où [latex]BF=\sqrt{2x-1}[/TeX][TeX]CF=1-BF=1-\sqrt{2x-1}[/TeX]
Coordonnées de quelques points clés:
A(0;0), B(1;0), E(x;0), F(1;[latex]\sqrt{2x-1}[/latex]), C(1;1), G(XG;1) et D(0;1).

Soient Aef et Afg les coefficient directeurs respectifs des droites (EF) et (FG).
Comme (EF) et (FG) sont perpendiculaires alors Aef*Afg=-1 or [latex]Aef=\frac{\sqrt{2x-1}}{1-x}[/latex] donc [latex]Afg=\frac{x-1}{\sqrt{2x-1}}[/latex]
L'équation de (FG):
[TeX]Y=\frac{x-1}{\sqrt{2x-1}}*X+\sqrt{2x-1}+\frac{1-x}{\sqrt{2x-1}} (1).[/TeX]
(La droite (FG) passe par F dont on connait les coordonnées )

A partir de (1), on détermine XG (abscisse de G) sachant que YG=1:
[TeX]XG=\frac{-x+\sqrt{2x-1}}{x-1}[/TeX]
En déduisons CG:
[TeX]CG=1-XG=\frac{2x-1-\sqrt{2x-1}}{x-1}[/TeX]
On remarque que [latex]CG=CF*\frac{\sqrt{2x-1}}{1-x}[/latex]

Pythagore dans CFG: [latex]FG^2=CG^2+CF^2[/latex]  soit  [latex]FG=\frac{x*CF}{1-x}[/latex] (le développement laissé au lecteur).
[TeX]HG=1-FG=\frac{1-2x+x\sqrt{2x-1}}{1-x}  (2)[/TeX]
Par définition du cercle inscrit dans un triangle:
[TeX]r=\frac{2*S}{p}[/latex]  où S et p sont respectivement l'aire et le périmètre du triangle; r étant le rayon du cercle inscrit.

[latex]2*S=CG*FC=FC^2*\frac{\sqrt{2x-1}}{1-x}=\frac{-2(2x-1)+2x\sqrt{2x-1}}{1-x}[/TeX][TeX]p=FC+CG+FG=2[/latex] (après tout développement bien fait, les expressions de FC, CG et FG en fonction de x sont données; bon calcul si vous voulez vérifier )

[latex]r=\frac{2*S}{p}=\frac{1-2x+x\sqrt{2x-1}}{1-x}  (3)[/TeX]
On déduit le rapport recherché:
[TeX]\frac{r}{HG}=\frac{(3)}{(2)}=1[/TeX]
Merci pour ce problème qui m'a fait gagner quelques connexions de neurones

Une autre méthode plus astucieuse

J'ai la flemme de tout réécrire en tapuscrit; donc je mets une photo du manuscrit

Bonjour,

Je passe par le point O, intersection du cercle et de FG.

OC=(1+racine(2))r (l'angle CDO vaut 45°)
OF=OG=1-x=OC (l'angle CFO vaut 45°)

D'où x=1-2(1+racine(2))r, 1 étant le coté du carré.

C'est tout simple où il y a un truc qui m'échappe ?

cogito, très joli problème en effet.

M'était complétement fourvoyé et j'avais aligné l'intersection O entre le cercle et FG avec le centre du cercle et le point C, ce qui est tout à fait faux si on fait un schéma plus général.

La solution est GH=r, j'y suis arrivé en forçant beaucoup et en passant par de l'Analyse , ce qui n'est pas une belle démonstration (mais je suis nul en géométrie).

En résumé, en notant x=AE/AB, 1-x=EB/AB, on trouve comment exprimer le rayon en fonction de x, avec L=AB
r=L/(1-x)(1-2x+x*racine(2x-1))

Il faut se servir du triangle FCG et montrer que le coté FG vaut FC+CG-2r, ce qui se fait simplement avec les propriétés du cercle inscrit.

En tenant compte du fait que FH est égal à AB, le segment FG vaut (L-y) où y est la valeur que que l'on cherche y=GH

En développant, on obtient aussi, après moultes simplifications,
y=L/(1-x)(1-2x+x*racine(2x-1))

Je n'ai pas tenu compte des propriétés du triangle GHI, il doit mener à une démonstration plus géométrique sans passer par la variable x.

J'attends de voir la belle solution géométrique ! Joli casse tête

Le temps de l'énigme arrive a sa fin.
Bravo à tous, et plus particulièrement à kossi_tg qui a sacrifié une soirée pour ce problème, et qui a donné deux démonstrations

Voici une solution :

Pour le début je vais reprendre l'explication de golgot59 :
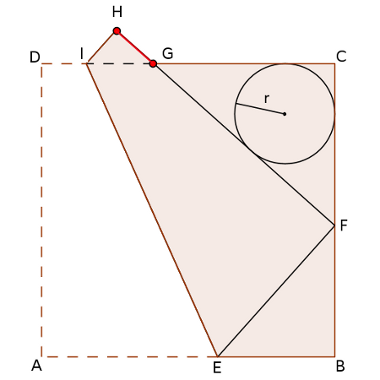
Supposons que le coté du carré soit égal à 1.
Soit a = EF et b = BF.

Alors on a :
  -EB = 1 - a.
  -En utilisant Pythagore dans le triangle EFB on obtient :
     a² = (1-a)² + b ² <->  a² = 1 -2a + a² + b²
       <-> b² = 2a - 1      (1)
       <-> a = (b² + 1)/2   (2).
   
  -Les triangle EFB et FCG sont semblables et de rapport FC/EB = (1-b)/(1-a), donc :
       -FC = 1-b = (1-a)(1-b)/(1-a)
       -FG = EF * (1-b)/(1-a) = a(1-b)/(1-a)
       -CG = BF * (1-b)/(1-a) = b(1-b)/(1-a)

Dans tous les calculs qui suivent, nous utiliserons (1), (2).
Maintenant on peut calculer d'une part HG :
   HG = 1 - FG = ((1-a) - a(1-b))/(1-a)  = ((1-2a) + ab)/(1-a) 
        = -2b² + (b²+1)b/(2(1-a)) = b(-2b + b² + 1)/(2(1-a))
        = b(1-b)²/(2(1-a)).

d'autre part on peut calculer r :
  comme CFG est rectangle en C on a :
   r = (1/2)*(CG + FC - FG) = (b(1-b) + (1 - a)(1-b) - a (1-b))/(2(1-a))
     = (b + (1 - 2a)) (1 - b)/(2(1-a)) = b(1-b)²/(2(1-a)).

On remarque ainsi que HG = r.

Bon, c'est vrai ça fait beaucoup de calcul.

C'est dommage que golgot59 se soit arrêté juste devant la ligne d'arrivé, mais
c'est un peu de ma faute, dans l'énoncé j'aurai du garder la question sous la forme : "démontrer que HG = r" plutôt que simplement "exprimer HG en fonction de r"