Forum dédié aux énigmes et à toutes formes de jeux de logique. | Déconnexion |
|
Tu n'es pas identifié sur Prise2tete : s'identifier.  Accueil Accueil
 Forum Forum
|
 |
#1 - 23-01-2014 14:57:33
D la suite dans les idées.Bonjour, cela fait un petit bout de temps que je ne sortais plus d'énigmes, mais voilà qu'à travers un exercice de math sur les suites niveau terminale s (voir première s) j'ai été confronté à un type de suite original qui m'a fait "méninger".
#0 Pub#2 - 23-01-2014 17:36:29
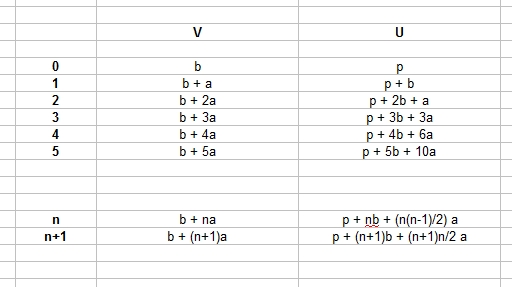
de la suite dand les idées.J’ai "bêtement" procédé par récurrence et je trouve: U(n) = (a/2).n² + (b - a/2).n + p #3 - 23-01-2014 18:11:02
de la suute dans les idées.1ère partie #4 - 23-01-2014 18:23:15#5 - 23-01-2014 20:46:00
de la suite dans les odées.Bonjour, Il aurait pu pleuvoir, con comme il est ! (Coluche) #6 - 24-01-2014 02:12:18#7 - 24-01-2014 16:16:59
de la suite dans les idézs.1ere partie : Réponse rapideSujets similaires
|
 | |||||||||||||||||||||||||||||||||
| Prise2Tete Forum Statistiques Liste des membres Hall of Fame Contact | |||||||||||||||||||||||||||||||||||
Un jeu où seules la réflexion, la logique et la déduction permettent de trouver la solution.