Bah alors on est pas inspiré ?

Oui masab c'est ce que je pense aussi mais je trouve que ca fait beaucoup

Voici l'une des solutions :

Je parle aux isométries (en 4D) près !

C'est-à-dire que je considère que deux tesseracts où chacun des sommets a les mêmes voisins ne représentent qu'une seule solution.

Pour compter les isométries : 16 choix pour la place du 1, puis 4!=24 choix pour les voisins du 1, ce qui fait 384 tesseracts isométriques pour chacune de mes 5 solutions.

384 x 5 = 1920. Nous sommes bien d'accord avec masab !

Voici la démonstration annoncée plus tôt :

Tout d'abord, la somme des sommets d'une face vaut 34, donc étant donnée une arête de somme x, il existe 3 autres arêtes parallèles à celle-ci de somme x, et encore 4 autres arêtes parallèles à celle-ci de somme 34-x.

On s'intéresse aux voisins possibles pour le sommet 1 :

Les sommets 2 à 7 ne peuvent être voisins de 1 :
Explications, par exemple, pour le 7 : si 7 est voisin de 1, cela donne une arête de somme x=8, or 8 ne peut être obtenu autrement que comme 2+6 ou 3+5. On ne peut donc trouver 3 autres arêtes de somme 8.

Le sommet 9 ne peut être voisin de 1 : si 9 est voisin de 1, cela donne une arête de somme x=10, or 34-x=24 ne peut être obtenu autrement que comme 16+8, 14+10 ou 13+11. On ne peut donc trouver 4 arêtes de somme 24 (parallèles à 1-9).

Le sommet 10 ne peut être voisin de 1 : si 10 est voisin de 1, il faut trouver 3 autres arêtes de somme x=11, et 4 autres arêtes parallèles à 1-10 de somme 34-x=23.
Or 23 ne peut être obtenu autrement que comme 16+7, 15+8, 14+9 ou 13+10.
Il n'y a donc pas le choix pour les 4 arêtes valant 23.
du coup, 11 ne peut être obtenu autrement que comme 5+6 (car 7, 8 et 9 sont déjà pris).
On ne peut donc trouver 4 arêtes de somme 23 et 3 autres arêtes de somme 11.

Le sommet 11 ne peut être voisin de 1 : si 11 est voisin de 1, il faut trouver 3 autres arêtes de somme x=12, et 4 autres arêtes parallèles à 1-11 de somme 34-x=22.
12 = 2+10 ou 3+9 ou 4+8 ou 5+7
22 = 16+6 ou 15+7 ou 14+8 ou 13+9 ou 12+10
Parmi les sommets {7, 8, 9, 10}, il y en a 3 dans des arêtes de somme 12, et au moins 3 dans des arêtes de somme 22. C'est impossible.
On ne peut donc trouver 4 arêtes de somme 22 et 3 autres arêtes de somme 12.

Le sommet 13 ne peut être voisin de 1 : si 13 est voisin de 1, il faut trouver 3 autres arêtes de somme x=14, et 4 autres arêtes parallèles à 1-13 de somme 34-x=20.
14 = 2+12 ou 3+11 ou 4+10 ou 5+9 ou 6+8
20 = 16+4 ou 15+5 ou 14+6 ou 12+8 ou 11+9
Si jamais il y avait l'arête 5-9 pour les 14, cela éliminerait les arêtes 15-5 et 11-9 pour les 20 et l'on ne pourrait alors en trouver 4 de somme 20.
De même pour l'arête 6-8.
Les arêtes de somme 14 sont donc 2-12, 3-11 et 4-10.
Cela laisse pour les arêtes de somme 20 : 15+5 et 14+6
On ne peut donc trouver 4 arêtes de somme 20 et 3 autres arêtes de somme 14.

Conclusion : Les seuls voisins possibles du 1 sont 8, 12, 14, 15 et 16. CQFD.

Bonjour

Le 1920 me laisse perplexe :

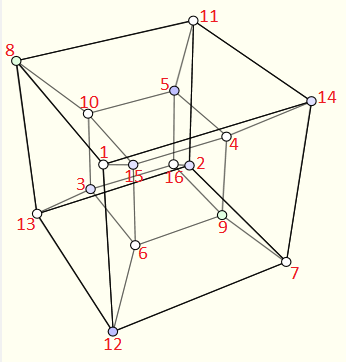
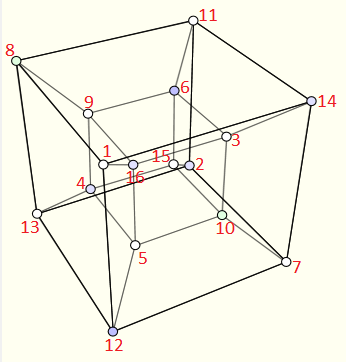
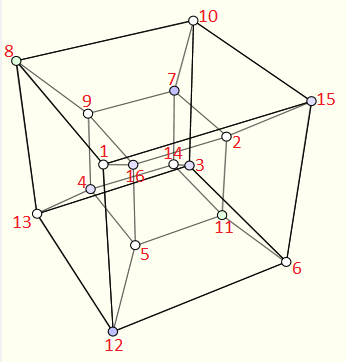
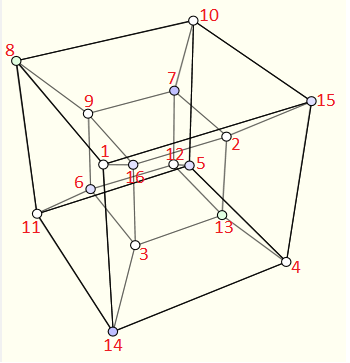
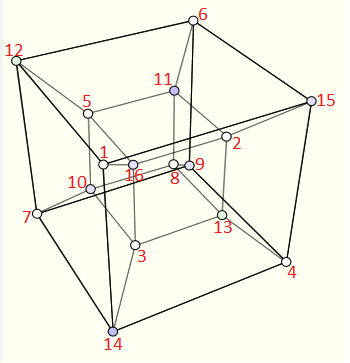
Comme on compte les solutions modulo les symétries et les rotations alors on peut de manière arbitraire placer le 1 sur un des 16 sommets du tesseract. Ensuite j'ai nommé les autres sommets par des lettres de a à o, comme dans la figure ci-dessous :



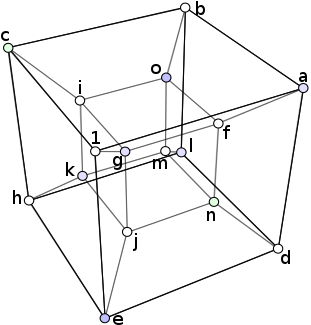
Détermination de la somme sur chaque face :

Soit x la valeur de la somme des quatre sommets d'une face.
Le fait que chaque face a la même somme nous donne les égalités suivantes :
x = 1 + a + b + c = f + g + i + o = j + k + m + n = d + e + h + l.

D'une part la somme total de tous les sommets est égal à la somme des nombres de 1 à 16 soit 16 * 17 / 2 = 8 * 17 = 136.

D'autre part la somme total de tous les sommets vaut :
1 + a + b + c + d + e + f + g + h + i + j + k + l + m + n + o =
(1 + a + b + c) + (f + g + i + o) + (j + k + m + n) + (d + e + h + l) = 4x.

Donc finalement 4x=136, soit x=34.

Détermination des solutions :

La connaissance des quatre valeurs a,c,e et g suffit à déterminer de manière unique la valeur de tous les sommets du tesseract.
En effet, si on regarde les différentes faces du cube on obtient les équations suivantes :

1 + a + b + c = 34 ----> b = 33 - a - c
1 + a + d + e = 34 ----> d = 33 - a - e
1 + a + g + f = 34 ----> f = 33 - a - g
1 + c + h + e = 34 ----> h = 33 - c - e
1 + g + i + c = 34 ----> i = 33 - g - c
1 + g + j + e = 34 ----> j = 33 - g - e
g + i + k + j = 34 ----> k = 34 - g - i - j
                   ----> k = 34 - g - 33 + g + c - 33 + g + e
                   ----> k = -32 + c + g + e
a + b + l + d = 34 ----> l = 34 - a - b - d
                   ----> l = 34 - a - 33 + a + c - 33 + a + e
                   ----> l = -32 + c + a + e
h + k + m + l = 34 ----> m = 34 - h - k - l
                   ----> m = 34 - 33 + c + e + 32 - c  - g - e + 32 - c - a - e
                   ----> m = 65 - g - c - a - e
j + g + f + n = 34 ----> n = 34 - j - g - f
                   ----> n = 34 - 33 + g + e - g - 33 + a + g
                   ----> n = -32 + e + a + g
i + g + f + o = 34 ----> o = 34 - i - g - f
                   ----> o = 34 - 33 + g + c - g - 33 + a + g
                   ----> o = -32 + c + a + g

Rappelons que les valeurs a à o représentent les nombre de 2 à 16.

On peut voir que une permutation des valeurs a,c,e et g entraîne :
  -Une permutation des valeurs b,d,f,h,i,j.
  -Une permutation des valeurs k,l,n,o.
  -Laisse m inchangé.

Ainsi aux permutations près on peut supposer a < c < e < g.

Donc pour chercher une solution il suffit de choisir 4 nombre parmi les 15 nombres de 2 à 16 pour les valeurs a,c,e et g et de voir si ça marche.
Le nombre de solution est donc bornée par le nombre de façon de choisir 4 nombre parmi 15 (désolé latex ne marche plus ) ce qui fait:
(12 * 13 * 14 * 15) / (2 * 3 * 4) = 13 * 7 * 15 = 1365.

Affinons un peu notre raisonnement. Regardons les équations trouvées pour les valeurs k,l,n et o :

k = -32 + c + g + e
l = -32 + c + a + e
n = -32 + e + a + g
o = -32 + c + a + g

Comme les valeurs de a à o sont les nombres de 2 à 16 on a chacune des 4 valeurs k, l, n et o qui sont supérieur ou égal à 2. Cela nous donne les quatres inégalités suivantes :
34 <= c + g + e
34 <= c + a + e
34 <= e + a + g
34 <= c + a + g

Remarquons également qu'il est impossible de faire de trois façons différentes 30 ou plus en additionnant deux nombres entiers plus petit que 16. On sait donc que a,c,e et g sont aux moins égaux à 4.

Maintenant faisons une étude de cas. Nous avons vu plus haut que l'on pouvait supposer que a < c < e < g.
Nous avons donc : 34 <= c + a + e  < c + a + g < e + a + g < c + g + e

Supposons donc a = 5 : On veut trouver c,e et g de façon à ce que :
29 <= c + e < c + g < e + g.
La seule solution possible est c = 14, e = 15 et g = 16.

On a donc a = 5 ; b = 33 - a - c = 33 - 5 - 14 = 14. On a donc b=c, ce qui n'est pas possible.

Supposons donc a = 6 : On veut trouver c,e et g de façon à ce que :
28 <= c + e < c + g < e + g.

On a deux solutions possibles :
c= 13, e=15, g = 16  ou c = 14, e = 15, g = 16

Avec la première solution on a j = 33 - g - e = 33 - 16 - 15 = 2 et l = - 32 + c + a + e = - 32 + 13 + 6 + 15 = 2 et donc j = l, ce qui est impossible.

Avec la deuxième solution on a i = 33 - g - c = 33 - 16 - 14 = 3 et l = -32 + c + a + e = - 32 + 14 + 6 + 15 = 3 et donc i = l, ce qui est impossible.

Pour résumer ces deux premiers cas, on a a,c,e et g qui sont au moins égal à 7.
Continuons :

Supposons donc a = 7 : On veut trouver c,e et g de façon à ce que :
27 <= c + e < c + g < e + g.

Il y a 5 solutions :

g = 16 , e = 15, c = 12 -> j = l -> pas possible.
g = 16, e = 15, c = 13 -> b = c -> pas possible.
g = 16, e = 15, c = 14 -> h = l -> pas possible.
g = 16, e = 14, c = 13 -> b = c -> pas possible.
g = 15, e = 14, c = 13 -> b = c -> pas possible.


Supposons donc a = 8 : On veut trouver c,e et g de façon à ce que :
26 <= c + e < c + g < e + g.

Il y a 8 solutions :

g = 16, e = 15, c = 11 -> j = l -> pas possible.
g = 16, e = 15, c = 12 ->
g = 16, e = 15, c = 13 -> i = l -> pas possible.
g = 16, e = 15, c = 14 ->
g = 16, e = 14, c = 12 ->
g = 16, e = 14, c = 13 -> j = l -> pas possible.
g = 15, e = 14, c = 12 ->
g = 15, e = 14, c = 13 -> i = n -> pas possible.


Ce qui nous fait 4 solutions pour a = 8 (je les résumerai à la fin).

Supposons donc a = 9 : On veut trouver c,e et g de façon à ce que :
25 <= c + e < c + g < e + g.

Il y a 14 solutions :

g = 16, e = 15, c = 10 -> j = l -> pas possible.
g = 16, e = 15, c = 11 -> a = d -> pas possible.
g = 16, e = 15, c = 12 -> b = c -> pas possible.
g = 16, e = 15, c = 13 -> a = d -> pas possible.
g = 16, e = 15, c = 14 -> a = d -> pas possible.
g = 16, e = 14, c = 11 -> f = h -> pas possible.
g = 16, e = 14, c = 12 -> b = c -> pas possible.
g = 16, e = 14, c = 13 -> i = l -> pas possible.
g = 16, e = 13, c = 12 -> b = c -> pas possible.
g = 15, e = 14, c = 11 -> a = f -> pas possible.
g = 15, e = 14, c = 12 -> i = n -> pas possible.
g = 15, e = 14, c = 13 -> j = l -> pas possible.
g = 15, e = 13, c = 12 -> b = c -> pas possible.
g = 14, e = 13, c = 12 -> b = c -> pas possible.

Supposons donc a = 10 : On veut trouver c,e et g de façon à ce que :
24 <= c + e < c + g < e + g.

Il y a 16 solutions :

g = 16, e = 15, c = 11 -> f = h -> pas possible.
g = 16, e = 15, c = 12 -> i = l -> pas possible.
g = 16, e = 15, c = 13 -> a = b -> pas possible.
g = 16, e = 15, c = 14 -> b = n -> pas possible.
g = 16, e = 14, c = 11 -> j = l -> pas possible.
g = 16, e = 14, c = 12 -> f = h -> pas possible.
g = 16, e = 14, c = 13 -> a = b -> pas possible.
g = 16, e = 13, c = 11 -> a = d -> pas possible.
g = 16, e = 13, c = 12 -> a = d -> pas possible.
g = 15, e = 14, c = 11 -> i = n -> pas possible.
g = 15, e = 14, c = 12 -> j = l -> pas possible.
g = 15, e = 14, c = 13 -> i = l -> pas possible.
g = 15, e = 13, c = 11 -> a = d -> pas possible.
g = 15, e = 13, c = 12 -> a = d -> pas possible.
g = 14, e = 13, c = 11 -> a = d -> pas possible.
g = 14, e = 13, c = 12 -> a = d -> pas possible.

Supposons donc a = 11 : On veut trouver c,e et g de façon à ce que :
23 <= c + e < c + g < e + g.

Il y a 10 solutions :

g = 16, e = 15, c = 12 -> h = l -> pas possible.
g = 16, e = 15, c = 13 -> m = n -> pas possible.
g = 16, e = 15, c = 14 -> b = l -> pas possible.
g = 16, e = 14, c = 12 -> i = l -> pas possible.
g = 16, e = 14, c = 13 -> h = l -> pas possible.
g = 16, e = 13, c = 12 -> j = l -> pas possible.
g = 15, e = 14, c = 12 -> f = h -> pas possible.
g = 15, e = 14, c = 13 -> h = l -> pas possible.
g = 15, e = 13, c = 12 -> f = n -> pas possible.
g = 14, e = 13, c = 12 -> i = k -> pas possible.

Supposons donc a = 12 : On veut trouver c,e et g de façon à ce que :
22 <= c + e < c + g < e + g.

Il y a 4 solutions :

g = 16, e = 15, c = 13 -> b = l -> pas possible.
g = 16, e = 15, c = 14 ->
g = 16, e = 14, c = 13 -> m = n -> pas possible.
g = 15, e = 14, c = 13 -> d = l -> pas possible.

Supposons donc a = 12 : On veut trouver c,e et g de façon à ce que :
22 <= c + e < c + g < e + g.

Ce qui fait donc 4 solutions pour a=8 et 1 solution pour a = 12 on arrive donc à 5 solutions qui sont (les solutions sont données dans "l'ordre alphabétiques") :
a  b   c   d   e  f  g  h  i  j k  l  m  n  o
8 13 12 10 15 9 16 6 5 2 11 3 14 7 4
8 11 14 10 15 9 16 4 3 2 13 5 12 7 16
8 13 12 11 14 9 16 7 5 3 10 2 15 6 4
8 13 12 11 14 10 15 7 6 4 9 2 16 5 3
12 7 14 6 15 5 16 4 3 2 13 9 8 11 10

Ah, ça y est, 1920 doit être le nombre de solutions total (sans compter les rotations et les symétries) car si on multiplie 5 par le nombre de permutations possibles de a,c,e et g on trouve 5 * 24 = 120 et comme le "1" a 16 position possible au départ, on obtient 120 * 16 = 1920 solutions au total.

Pouf, je n'ai sûrement pas fait au plus simple, mais on est quand même arrivé au bouts