|
#1 - 26-11-2014 10:22:39
- unecoudée
- Professionnel de Prise2Tete
- Enigmes résolues : 0
- Messages : 319
A côté coule une rivire.
bonjour à tous.
J'ai vu que laTex refonctionnait . Alors je propose une autre petite énigme que voici:
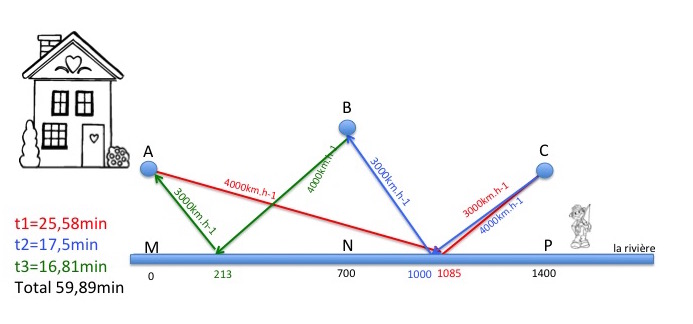
Paul est à la retraite , habite une fermette pas très loin de la rivière . Il dispose de 3 bassins pour diverses choses jardin , animaux...
La maison , ainsi qu'un premier bassin se trouvent en A situé à 300 m de la rivière ; dans sa région la rivière coule en ligne droite .
Le second bassin est en B à 400 m de la rivière et à [latex]\frac{\sqrt{2}}{2} [/latex] km de A .
Le troisième et dernier bassin est en C , à 300 m de la rivière et à [latex]\frac{\sqrt{2}}{2} [/latex] km de B ; le bassin C est donc à plus d'un km du bassin A .
Tous les jours et pour s'entretenir physiquement , Paul prend ses 2 arrosoirs , se dirige vers la rivière , les remplit et les vide une fois dans chacun des 3 bassins.
Il a donc 3 transferts à effectuer chaque jour.
pour résumer , si M , N & P sont 3 points au bord de la rivière , Paul effectuera par exemple les parcours A M B N C P A ou A M A N B P C A . par exemple.
Paul marche à vitesses constantes : 4 km/h avec arrosoirs vides et 3 km/h avec arrosoirs pleins .
Aussi ses temps de remplissage et de vidage d'arrosoir sont négligeables.
Et il est avare de son temps.
quel temps minimum peut-il espérer réaliser lors de sa promenade quotidienne de son départ de A à son retour en A ?
bonne route .
#2 - 26-11-2014 14:09:48
- SabanSuresh
- Elite de Prise2Tete
- Enigmes résolues : 45
- Messages : 1951
- Lieu: Paris
a côté coyle une rivière.
Assez compliqué ...
La distance AC vaut 1.4km.
Je trouve comme temps :
(4,24/4+5,25/3+5/4+5/3+(41/3)/4+(18,5/6)/3)/10 = 0,995 = 1 h
Le "/10", c'est parce que je comptais en hectomètres. Mon trajet c'est AMBNCPA avec M tels que AMB rectangle en M, N tel que BNC rectangle en N et P tel que CPA rectangle en P. Mais je suis pas sûr de ma méthode.
Je suis pas du tout sûr de ma réponse ...
#3 - 26-11-2014 16:46:52
- nobodydy
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 1677
A côté cooule une rivière.
#4 - 26-11-2014 16:50:21
- halloduda
- Professionnel de Prise2Tete
- Enigmes résolues : 24
- Messages : 495
- Lieu: Ardèche
A côté coule ne rivière.
Je trouve 1 heure 03 mn 21.6 s
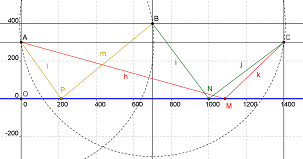
Coordonnées des points successifs
A 000, 300
M 1086.104, 0
B 700, 400
N 1000, 0
C 1400, 300
P 213.28, 0
A 000, 300
#5 - 26-11-2014 17:22:33
- golgot59
- Elite de Prise2Tete
- Enigmes résolues : 48
- Messages : 1494
- Lieu: Coutiches
a côté coule une rivièrr.
Salut !
Bon, j'ai la flemme et pas le temps de tout rédiger bien proprement, mais voici la méthode que j'emploierai :
Je fais un petit dessin, je calcule la distance parallèlement à la rivière qui sépare les villes A et C de B par pythagore : 700m.
Ensuite je trace les symétriques A', B' et C' par rapport à la rivière, et je reporte les distances : Les bonnes côté ABC, et en proportion des vitesses "ralenties", c'est à dire à 3km/h au lieu de 4km/h de l'autre côté.
Enfin je trace AB'CA', qui me donne des points sur la rivière, là où remplir les seaux. Bien sûr il faut refaire un petit schéma à chaque trajet pour aligner les villes.
Je ne sais pas si c'est bien clair, ni si c'est la meilleure méthode, mais c'était pour participer 
#6 - 26-11-2014 18:03:01
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
a côté coule unr rivière.
Sauf erreur , aucun problème mais plutôt pénible à calculer .
Pour chaque descente et remontée ( elle sont indépendantes ) il faut minimiser 3.rouge+4.bleu .
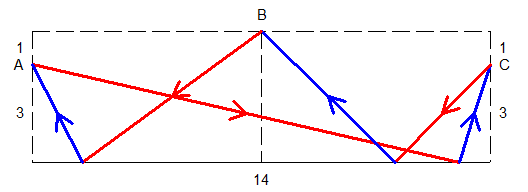
Vasimolo
#7 - 26-11-2014 20:48:11
- Franky1103
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 3238
- Lieu: Luxembourg
A côté coule un erivière.
Distance entre M et N (= distance entre N et P) = V(0,50-0,01) = 0,7 km
Temps mis entre A et B = t1(x) = (1/4).V(x²+0,09) + (1/3).V((0,7-x)²+0,16)
t1’(x) = (1/4).(x)/V(x²+0,09) + (1/3).(x-0,7)/V((0,7-x)²+0,16)
t1’(x) = 0 pour x = 0,4 et t1(0,4) = 7/24 = 0,291667
Temps mis entre B et C = t2(x) = (1/4).V(x²+0,16) + (1/3).V((0,7-x)²+0,09)
t2’(x) = (1/4).(x)/V(x²+0,16) + (1/3).(x-0,7)/V((0,7-x)²+0,09)
t2’(x) = 0 pour x = 0,486718 et t2(0,486718) = 0,280195
Temps mis entre C et A = t3(x) = (1/4).V(x²+0,09) + (1/3).V((1,4-x)²+0,09)
t3’(x) = (1/4).(x)/V(x²+0,09) + (1/3).(x-1,4)/V((1,4-x)²+0,09)
t3’(x) = 0 pour x = 1,086103 et t3(1,086103) = 0,426427
En sommant tout, on arrive à un temps de: 0,998289,
soit: 59 mn 53,84 sec (un peu moins d’une heure)
Édit: Si on le fait proprement, alors on tombe à chaque fois sur une équation du 4è degré sans racine évidente. Du coup, pour annuler les dérivées, j'y suis carrement allé à la machette dichotomique.
#8 - 26-11-2014 20:57:40
- unecoudée
- Professionnel de Prise2Tete
- Enigmes résolues : 0
- Messages : 319
a côté coule une tivière.
salut.
Bien vu franky .
pour les autres .
merci pour les shémas . il n'y a qu'un angle droit et un seul . mais alors pourquoi ?
Il faut effectivement optimiser . comment ?
on doit descendre juste en dessous de l'heure . avec quelle stratégie ?
#9 - 27-11-2014 17:26:12
- gilles355
- Professionnel de Prise2Tete
- Enigmes résolues : 49
- Messages : 421
A côté coulle une rivière.
Salut je trouve 65 minutes pour l'instant, tu dis en dessous de l'heure ? Je vais y réfléchir ce soir...
#10 - 27-11-2014 21:06:25
- NickBern
- Passionné de Prise2Tete
- Enigmes résolues : 45
- Messages : 50
#11 - 28-11-2014 09:45:30
- nobodydy
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 1677
A côt coule une rivière.
Il est avare de son temps mais pas de son argent
il déplace les bassins et fabrique 2 ponts
mais cela ne marche pas non plus  car AC n'est pas supérieur à 1km (AC=1km) car AC n'est pas supérieur à 1km (AC=1km)
je crois que je vais attendre la réponse
Bonne journée
#12 - 28-11-2014 20:44:07
- gilles355
- Professionnel de Prise2Tete
- Enigmes résolues : 49
- Messages : 421
A côté coule une rivièer.
Bon comme y a 2 arrosoirs j'imagine qu'il faut peut être utilisé qu'un seul arrosoir parfois, donc à ce moment là la vitesse serait de 3,5 km/h.
Je trouve pas encore un chemin optimal mais je cherche ...
Edit : J'ai trouvé 62 minutes en passant en point intermédiaire par le milieu je vais encore chercher ...
Re edit : Ca y'est !!!!!! il fallait aussi l'appliquer une troisième fois, je trouve 59.84923998 minutes !!!!
J'ai plus qu'à mathématiser formellement tout ça maintenant 
#13 - 28-11-2014 22:49:21
- gilles355
- Professionnel de Prise2Tete
- Enigmes résolues : 49
- Messages : 421
A côtté coule une rivière.
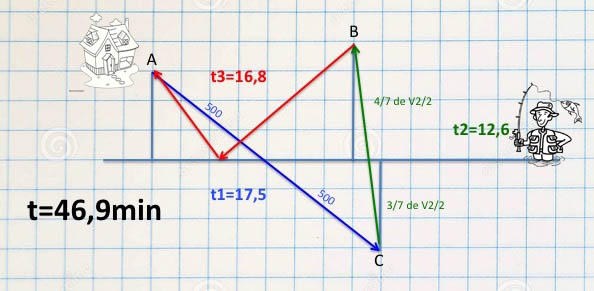
J'ai pas eu la fois de calculer des dérivées de pleins de racine carrées dans tous les sens donc j'ai résolu graphiquement.
Par contre j'ai écris les équations.
http://www.prise2tete.fr/upload/gilles355-riviere.jpg
Je trouve donc environ 59,85 minutes !
#14 - 29-11-2014 09:30:22
- unecoudée
- Professionnel de Prise2Tete
- Enigmes résolues : 0
- Messages : 319
z côté coule une rivière.
bonjour.
à gille355: il en manque un tout ptit peu.
#15 - 29-11-2014 10:57:24
- NickBern
- Passionné de Prise2Tete
- Enigmes résolues : 45
- Messages : 50
a vôté coule une rivière.
Ah mince il avait 2 arrosoirs 
Et je me suis limité aux points M,N,P sur la rivière, mais c'est vrai qu'il peut remplir partout...
#16 - 29-11-2014 11:29:58
- unecoudée
- Professionnel de Prise2Tete
- Enigmes résolues : 0
- Messages : 319
Acôté coule une rivière.
salut.
et merci d'avoir participé .
ma résolution est prête , mais gros problèmes avec latex . si je la balance , la moitié seulement sera lisible . si vous la voulez maintenant pas de souci .
#17 - 29-11-2014 12:17:02
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
a côté couke une rivière.
D'un autre côté la solution proposée par Gilles dans le message #13 donne le schéma de la solution . On peut tout à fait se contenter d'une valeur approchée de la solution , le calcul exact de celle-ci ne posant pas d'autre problème que celui d'être long et fastidieux 
Une variante à faire peur ( ou pas ) 
Avec un seul arrosoir plein Paul se déplace à 3,5 km/h , il peut poser un arrosoir sur son trajet et le récupérer quand il repasse par ce point . Peut-il faire mieux ?
Vasimolo
#18 - 29-11-2014 12:34:18
- unecoudée
- Professionnel de Prise2Tete
- Enigmes résolues : 0
- Messages : 319
A ôcté coule une rivière.
résolution.
dans ce problème se succèdent trois phases identiques concernant le calcul du chemin le plus rapide .
phase (1) A M B avec a = ordonnée de A , b l'ordonnée de B et h la différentielle X de A & B , ---> A(0,a) , M(x,0) & B(h,b) pour les coordonnées.
phases (2) & (3) B N C & C P A ou seront utilisés les mêmes paramètres a b & h , mais leurs valeurs seront différentes .
a) Phase (1) pour ce premier prélèvement d'eau l'équation du temps s'écrit:
[TeX]t_{x} = \frac{\sqrt{x^2+a^2}}{v_1} + \frac{\sqrt{(h-x)^2 + b^2}}{v_2}[/TeX]
avec [latex]v_1=4[/latex] et [latex]v_2=3[/latex]
en dérivant cette fonction on doit trouver un extrémum pour t'(x) = 0
[TeX]t'_{x} = \frac{x}{v_1.\sqrt{x^2+a^2}} - \frac{h-x}{v_2.\sqrt{(h-x)^2 + b^2}}[/TeX]
en divisant sous le premier radical par a² et sous le second radical par b² :
[TeX]t'_{x} = \frac{x}{v_1.a.\sqrt{\frac{x^2}{a^2}+1}} - \frac{x - h}{v_2.b.\sqrt{\frac{(h-x)^2}{b^2} + 1}} [/TeX]
si de M , je trace la demi droite [My ) , j'obtiens 2 angles : [latex]\widehat{AMy} = \alpha[/latex] puis [latex]\widehat{BMy} = \beta[/latex]
et [latex]1+\frac{x^2}{a^2} =1+ \tan²{\alpha} = \frac{1}{\cos²{\alpha}}[/latex]
[TeX]1+\frac{(h-x)^2}{b^2} =1+ \tan²{\beta} = \frac{1}{\cos²{\beta}}[/TeX]
et de même hors des radicaux on aperçoit:
[TeX]\frac{x}{a} = \tan{\alpha}[/TeX]
et: [latex]\frac{h-x}{b} = \tan{\beta}[/latex]
et la dérivée s'écrit : [latex]t'_{x} = \frac{\sin{\alpha}}{v_1} - \frac{\sin{\beta}}{v_2} = \frac{x}{4.\sqrt{x^2+a^2}} - \frac{h - x}{3\sqrt{(h-x)^2+b^2}} = 0[/latex]
[TeX]t'_{x} = \frac{\sin{\alpha}}{v_1} - \frac{\sin{\beta}}{v_2} = 0 \Rightarrow v_2.\sin{\alpha} = v_1.\sin{\beta}[/TeX]
qui conduit à [latex]\frac{\sin{\beta}}{\sin{\alpha}} = \frac34[/latex] et pour les 2 autres transferts d'eau :
[TeX] \frac{\sin{\Gamma}}{\sin{\Delta}} = \frac{\sin{\Phi}}{\sin{\Psi}} = \frac34 [/TeX]
dans la recherche de la racine réelle de P(x) = 0 il suffira d'affecter leur valeur propre à chacun des paramètres a , b & h pour avoir les bons coefficients du polynôme
[TeX]\begin{cases}phase(1)&a=0.3 ; b=0.4 ; h=0.7\\phase(2)&a=0.4 ; b=0.3 ; h=0.7\\phase(3)&a=0.3 ; b=0.3 ; h=1.4\end{cases}[/TeX]
on a donc l'égalité suivante:
[TeX]3x.\sqrt{(h-x)^2 + b^2} = 4.(h-x).\sqrt{x^2 + a^2}[/TeX]
après élévation au carré pour faire disparaître les radicaux on obtient :
[TeX]9x^2.\left[x^2 + h^2 - 2hx + b^2\right] = \left[16h^2 + 16x^2 - 32hx\right].\left[x^2 + a^2\right][/TeX]
et le polynôme suivant:
[TeX]7.x^4 - 14h.x^3 + (7h^2 + 16a^2 - 9b^2).x^2 - 32ha^2.x + 16h^2a^2 = 0[/TeX]
donne x=0.4 et dans ce cas seulement on en déduit la mesure des 2 segments AM & MB : 0.5 , hypoténuse des 2 triangles rectangles de côtés 0.3 , 0.4 & 0.5
par contre le triangle AMB , lui , est isocèle rectangle : [latex] 0.5 ; 0.5 ; 0.5\sqrt{2}[/latex]
en résumé les 3 polynômes à résoudre seront:
phase(1) [latex] 7x^4 - 9.8x^3 + 3.43x^2 - 2.016x + 0.7056 = 0 [/latex] avec a=0.3 , b=0.4 & h=0.7
phase(2) [latex] 7x^4 - 9.8x^3 + 5.18x^2 - 3.584x + 1.2544 = 0 [/latex] avec a=0.4 , b=0.3 & h=0.7
phase(3) [latex] 7x^4 - 19.6x^3 + 14.35x^2 - 4.032x + 2.8224 = 0 [/latex] avec a=0.3 , b=0.3 & h=1.4
donne les 3 valeurs de x correspondantes aux 3 phases: 0.4 , 0.48671839 & 1.086103
et les valeurs (h-x) correspondantes 0.3 , 0.2132816 & 0.313897
les 2 segments parcourus durant chacune de ces 3 phases :
phase(1) AM = 0.5 & MB = 0.5 ; phase(2) BN = 0.63 & NC = 0.3680884 ; phase(3) CP = 1.126774 , PA = 0.4342
et on peut vérifier pour chacune des phases le rapport des sinus qui est égal à 3/4
le temps total : [latex] \frac{0.5 + 0.63 + 1.126774}{4} + \frac{0.5 + 0.3680884 + 0.4342}{3} \approx 0.9982896333 h[/latex]
qui donne 0h 59min 53.84 s
en espérant avoir été clair.
Mots clés des moteurs de recherche
|
 |

 Accueil
Accueil
 Forum
Forum