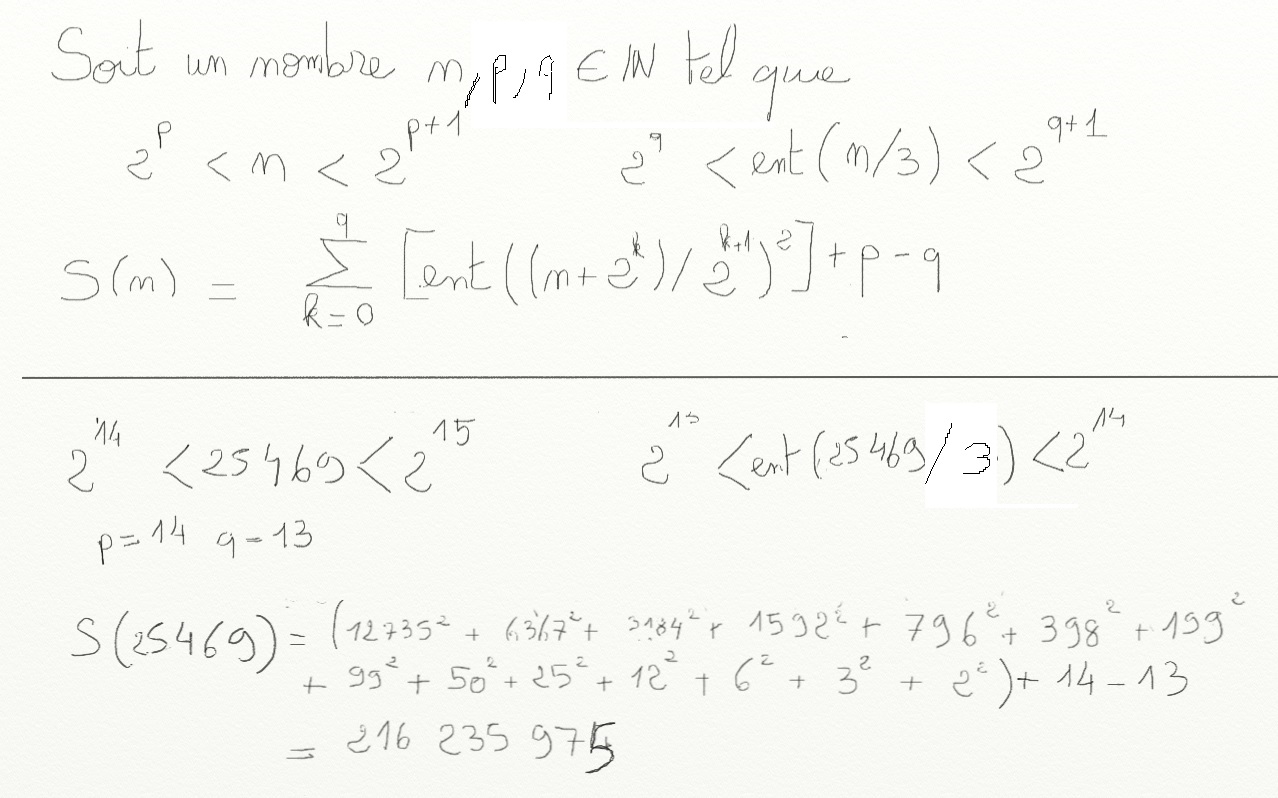Enigme Somme d'impairs @ Prise2Tete

nodgim · #1

Bonjour à tous,
Un petit problème pas bien méchant. Pour un nombre n donné, on se propose de calculer la somme SI(n) de 1 à n, mais en ôtant aux nombres pairs leur parité (pour 36--->9, pour 26--->13, etc).
Exemple SI(10)=1+1+3+1+5+3+7+1+9+5=36.

Calculer SI(25469), par exemple, avec un crayon et un papier.

cogito · #2

Bonjour

On peut partitionner la somme des nombres de 1 à n en la somme des nombres impairs plus la somme des nombre pairs.

Dans SI(n) la somme des nombres impairs reste inchangé
De plus nous avons 2+4+6+...+2k = 2*(1+2+3+...+k), comme le facteur 2 n'est pas compté, il suffit de calculer SI(k) et de l'ajouter à la somme des nombres impairs pour avoir le résultat final.

Soit donc Si(n) la somme des nombres impairs plus petit que n.

On sait que :
* Si(2k)=k²
* Si(2k+1)=(k+1)²

On a également :
* SI(1)=1
* SI(2k)=Si(2k)+SI(k) = k² + SI(k)
* SI(2k+1)=Si(2k+1)+SI(k) = (k+1)² +SI(k)

Par exemple pour SI(10) nous avons :

SI(10)=5²+SI(5)=25+(2+1)²+SI(2)=25+9+1²+SI(1)=25+9+1+1=36 on retombe bien sur le même résultat.

Donc maintenant pour 25469 :

SI(25469)
Spoiler : Détails du calcul
=216235975

modulo les erreurs de calcul évidemment

à noter que la somme "normale" ferait 324347715 on a donc gagner (ou perdu) 108111740 soit 100 millions à peu près.

gwen27 · #3

A mon avis, cela fait juste des suites imbriquées de nombres impairs

Donc, 1 3 5 7 ... -> 25469
Plus 1 3 5 7 ....-> 25469/2 = 12734 (12733)
Plus 1 3 5 7 ...-> 12734/2 = 6367
Plus 1 3 5 7 ...-> 3183
Plus 1 3 5 7 ...-> 1591
Plus 1 3 5 7 ...-> 795
Plus 1 3 5 7 ...-> 397
Plus 1 3 5 7 ...-> 198 (197)
Plus 1 3 5 7 ...-> 99
Plus 1 3 5 7 ...-> 49
Plus 1 3 5 7 ...-> 24 (23 )
Plus 1 3 5 7 ...-> 12 (11)
Plus 1 3 5 7 ...-> 6 (5)
Plus 1 3 5 7 ...-> 3
Plus 1 3 5 7 ...-> 1

210 118 975 ?

Quelques doutes plus tard sur les calculs : 216 235 975

nodgim · #4

Sans surprise, c'est OK pour Cogito et Gwen.

shadock · #5

Je ne comprends pas comment du calcul ta somme en enlevant aux nombres pairs leur parité. En prenant le même exemple pour n=10 tel que je comprends l'énoncé il faut faire ça :

SI(10)=1+1+3+3+5+5+7+7+9+9... ôter un à tous les nombres pairs pour qu'ils deviennent impairs et perdent ainsi leur parité ...

nodgim · #6

Shadock, j'ai donné 2 exemples : 36---->9 et 26----->13.
On ôte la parité des nombres en divisant par 2 autant de fois que nécessaire.

unecoudée · #7

salut à tous.

ma réponse , si je n'ai rien oublié en route :

1 + 2² + 3² + 6² + 12² + 25² + 50² + 99² + 199² + 398² + 796² + 1592² + 3184² + 6367² + 12735² = 216235975

gilles355 · #8

Salut, pour l'instant j'ai trouvé que S(2^n) = (4^(n) - 1)/3 +1

Je cherche encore pour le reste.

Franky1103 · #9

J’additionne d'abord tous les nombres impairs de 1 à 25469, qui est la moyenne de ces deux extrêmes au carré, soit 12735^2. Je divise ensuite les nombres qui restent par 2 et je procède de la même manière jusqu’à finir sur 1.
La somme cherchée est donc:
12735^2 + 6367^2 + 3184^2 + 1592^2 + 796^2 + 398^2 + 199^2 + 99^2 + 50^2 + 25^2 + 12^2 + 6^2 + 3^2 + 2^2 + 1^2 = 216 235 975

nodgim · #10

2 nouvelles réponses correctes pour Unecoudée et Francky1103, bravo !

Pour Gilles355: c'est bon, mais tu ne trouveras pas une réponse aussi synthétique pour un nombre quelconque.

Sydre · #11

SI(n) est une somme de sommes d'impairs consécutifs.

Sachant que la somme des k premiers impairs vaut k^2 on en déduit que SI(n) se met sous la forme d'une somme de carrés.

En plus de la première somme, on démarre une nouvelle somme d'impairs consécutifs à chaque puissance de 2.

La somme d'impairs consécutifs d'ordre k comporte [1/2+n/2^k] termes. Ou [] représente la fonction partie entière.

Pour calculer SI(n) il suffit donc de :

- Déterminer p, la puissance de 2 la plus grande qui minore n.

- Calculer SI(n) = [1/2+n/2]^2+...+[1/2+n/2^(p+1)]^2

Pour SI(25469) cela donne :

- p = 14

- SI(25469) = 12735^2+6367^2+3184^2+1592^2+796^2+398^2+199^2+99^2+50^2+25^2+12^2+6^2+3^2+2^2+1 = 216235975

scarta · #12

Si on part de la somme totale, il faut oter la moitié des multiples de 2 mais pas de 4, 3/4 des multiples de 4 mais pas de 8, etc...
Ou plus simplement, otons la moitié pour tous les nombres pairs, le quart des multiples de 4, etc...
Pour un nombre de la forme (2P+1)*2^n, on en aura oté 1/2 + 1/4 + ... soit (2^n-1 + 2^n-2 + ... +1)/2^n = (2^n-1)/2^n

Pratiquement, on part de N(N+1)/2, puis on pose X=N. Tant que X > 0, on ote à notre résultat E(X/2)E(X/2 + 1)/2 et on pose X = E(X/2), avec E l'arrondi à l'entier inférieur ou égal

En plus ça se factorise bien si on le fait à la main, pour éviter des calculs barbares.
Bref, on trouve 324347714

gilles355 · #13

216 235 975

Alors j'ai trouvé une formule à voir dans la pièce jointe.
Je l'ai testé pour les 49 premiers nombre et elle marche, j'espère ne pas avoir fait d'erreur de calcul pour le nombre 25469 mais je suis sûr de la formule.

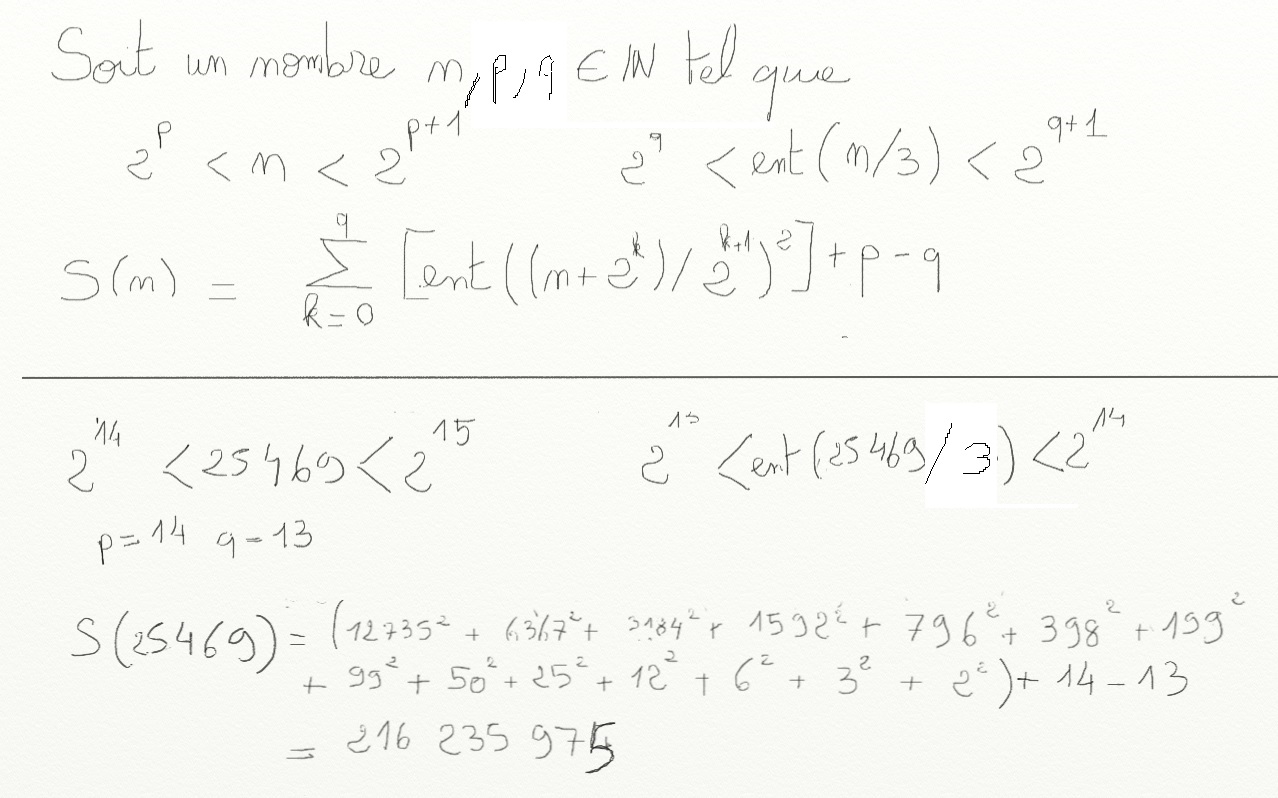
http://www.prise2tete.fr/upload/gilles355-eninb.jpg

scarta · #14

Me suis planté dans mon calcul : 216235975

Autre approche que celle que j'ai déjà donnée : on compte les nombres impairs (somme = E(N/2)², puis on ajoute la moitié des nombres de la forme 2*(2p+1), donc encore une somme d'impairs, etc...
Au final, on part d'un nombre, on divise par 2, on arrondit, et on ajoute le carré au total, puis on continue avec la moitié de ce nombre, ...
Au final, on calcule donc 12735²+6367²+3184²+1592²+796²+398²+199²+99²+50²+25²+12²+6²+3²+2²+1²
Et on trouve le même résultat (ce qui m'a au passage rendu service, puisque j'ai vue que le m'étais planté sur celui du dessus)

nodgim · #15

Bravo à Sydre, Scarta et Gilles355 qui ont aussi trouvé le bon résultat !

Une question subsidiaire: Vers quoi tend le rapport SI(n)/S(n), S(n) étant la somme de 1 à n, qiuand n tend vers l'infini ?

Franky1103 · #16

Question subsidiaire:
Désolé, mais je ne sais pas écrire avec latex, qui d’ailleurs marche mal
SI(n) = Somme[(n/2^n)²] = n².Somme[2^(-2n)]
et Somme[2^(-2n)] tend vers 1/3 quand n tend vers +oo
S(n) = n.(n+1)/2 = n².(1+1/n)/2
et (1+1/n)/2 tend vers 1/2 quand n tend vers +oo
Donc SI(n)/S(n) tend vers 2/3 quand n tend vers +oo

Edit: On le voit d'ailleurs sur l'exemple, puisque 25469 est presque l'infini
SI(25469) = 216 235 975 et S(25469) = 324 347 715, avec un rapport de presque 2/3

unecoudée · #17

salut.

le rapport SI(n)/S(n) doit tendre vers 2/3 lorsque n tend vers l'infini

nodgim · #18

Bravo à tous pour vos réponses. Oui, SI(n)/S(n) tend bien vers 2/3. Autrement dit, la contribution des facteurs 2 est dans la proportion de 1/3 du total.

Forum dédié aux énigmes et à toutes formes de jeux de logique.	Déconnexion
Tu n'es pas identifié sur Prise2tete : s'identifier. Accueil Forum	[+]

#1 - 06-12-2014 10:28:42

oSmme d'impairs

#0 Pub

#2 - 06-12-2014 13:43:05

Somme d'impair

#3 - 06-12-2014 15:11:04

Soomme d'impairs

#4 - 06-12-2014 19:34:01

Some d'impairs

#5 - 07-12-2014 01:40:18

Somme d'impaiirs

#6 - 07-12-2014 09:50:37

Somme d'iimpairs

#7 - 07-12-2014 10:29:27

SSomme d'impairs

#8 - 07-12-2014 14:46:58

Somme d'imparis

#9 - 07-12-2014 14:58:21

Smme d'impairs

#10 - 07-12-2014 18:00:50

Somme d'ipairs

#11 - 07-12-2014 18:50:36

Somme d'ipairs

#12 - 07-12-2014 20:53:34

somme d'impaurs

#13 - 07-12-2014 22:35:57

Somme d'impiars

#14 - 08-12-2014 13:01:58

somme d'impaits

#15 - 08-12-2014 19:49:58

qomme d'impairs

#16 - 08-12-2014 22:22:59

Somme dd'impairs

#17 - 09-12-2014 09:02:24

somme d'impaors

#18 - 09-12-2014 18:45:04

Somme d'ipairs

Réponse rapide

Sujets similaires

Mots clés des moteurs de recherche

Pied de page des forums