 |
#1 - 09-12-2014 09:52:37
- unecoudée
- Professionnel de Prise2Tete
- Enigmes résolues : 0
- Messages : 319
Petiit exercice (I)
bonjour à tous .
a) les impératifs
utiliser une seule fois , mais tous , chacun des chiffres 0 1,2,3,4,5,6,7,8,9
b) les interdits :
- les 4 opérateurs - , + , / , x sont interdits
exemple: 2sin45.cos45 ou le produit est utilisé 2 fois .
4^(1/2)
- la fonction partie entière
c) sont autorisés :
-- les fonctions habituelles que l'on trouve sur les calculettes de collégiens
ex. les fonctions trigos avec leurs réciproques , les logarithmes en toute base ,
parce que celles ci existent sur certains modèles de calculette . la fonction mise au carré x^2 ainsi que la la fonction x^(-1) , ou 1/x , la racine carrée . pour ces 3 fonctions les chiffres 1 et 2 et le signe - ne seront pas pris en compte .
pour résumer [ (sin0)^-1 ]² seul le zéro a été utilisé .
-- les écritures 125,7 89 3 43^20 log en base 12 sin720°
-- les constantes mathématiques usuelles pi & e , l'imaginaire i
ex: la racine carrée de (145^9.8 ) le chiffre 2 n'a pas été utilisé.
d) la question: trouver les premiers entiers 1 , 2 .. pour commencer .
je donne un exemple: sin(1234567890°) = 1 , mais on peut trouver 1 avec une autre méthode .
s'il manque des infos n'hésitez pas .
bonne prise 2 tête.
l'abus d'aspirine .....
#2 - 09-12-2014 19:11:29
- cogito
- Expert de Prise2Tete
- Enigmes résolues : 48
- Messages : 593
Petit eexrcice (I)
Bonjour,
j'ai quelques petites questions :
-Est-ce que dans "log en base 12 de 3" on peut dire que 1 et 2 ont été utilisés ?
-Il existe aussi la fonction x^3 sur certaines calculatrices, mais elle n'a pas été cité, est-ce qu'on y a le droit ?
-A-t-on le droit aussi à pgcd et ppcm ?
-Les fonctions trigonométriques sont-elles forcément utilisées avec des degrés ou bien peut-on aussi les utiliser avec des radians ?
Désolé, mais il faut souvent que je pose plein de questions avant de commencer une énigme 
EDIT : le signe "-" est interdit en tant que soustraction, mais est-il aussi interdit en tant que signe d'un nombre négatif ?
Il y a sûrement plus simple.
#3 - 09-12-2014 20:39:14
- unecoudée
- Professionnel de Prise2Tete
- Enigmes résolues : 0
- Messages : 319
petit exrrcice (i)
salut.
cogito : log en base 12 de 3 utilise 1 , 2 & 3
si la fonction x^3 existe sur ta calculette , c'est une fonction spécifique , alors dans ce cas 3 n'est pas utilisé , pour info , je n'utilise pas cette fonction .
si tu utilises la trigo , alors autant préciser l'unité angulaire .
quant aux ppcm & pgcd , non! tout comme la partie entière .
le problème est de généraliser une formule afin de trouver une valeur n (entier positif donc) comme 1 , 2 , 3 ...etc
j'ai d'ailleurs un second problème du même genre à proposer avec d'avantage d'interdits.
#4 - 09-12-2014 22:47:13
- golgot59
- Elite de Prise2Tete
- Enigmes résolues : 48
- Messages : 1494
- Lieu: Coutiches
Petitt exercice (I)
Salut !
Pour l'instant j'ai ça :
sin(1234578960°)=0
123456789^0=1, ou cos(1234578960°)=1
(inv[sin(1043678925°)])²=2
(inv[sin²(1043678925°)])²=4
#5 - 10-12-2014 10:10:48
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 6,194E+3
petit exercuce (i)
Un truc du genre, c'est valable ?
Je crois que ça permet déjà de généraliser assez loin , non ?
Ca pose juste un souci pour les nombres utilisant 0,2,4,6, et 8
Et pour ceux utilisant deux fois le même chiffre... (le 0 est à la place du PI ou dans le nombre)
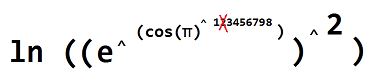
#6 - 10-12-2014 16:25:31
- unecoudée
- Professionnel de Prise2Tete
- Enigmes résolues : 0
- Messages : 319
Petit xercice (I)
salut.
golgot et gwen : merci pour votre persévérance
golgot: bien vu avec 0 , 1 , 2 & 4
gwen : les exposants 2 et -1 sont utlisés pour les touche x² et 1/x
tu peux donc utiliser les chiffres 1 et 2 ailleurs . donc avec tes 2
exposants dans ta formule tu as déjà pas mal de possibilités. les solutions possibles seraient toutes les valeurs de ton second exposant.
Spoiler : [Afficher le message] en fait avec une itération il y a une formule pour trouver tout entier N
#7 - 10-12-2014 19:52:22
- cogito
- Expert de Prise2Tete
- Enigmes résolues : 48
- Messages : 593
petit exzrcice (i)
Pour l'instant j'ai :
0 = 0 ^123456789
1 = 1 ^ 234567890
2 = 2^(134567890^(sin pi radian))
en utilisant cette technique je peux faire beaucoup d'entier, comme (sin pi radian = 0) alors x^(sin pi radian)= 1 et donc n=n^(x^(sin pi radian)). où x contient tous les chiffres non utilisés dans l'écriture de n.
Mais ceci ne fonctionne que pour un nombre fini d'entiers.
Et ça ne marche pas pour 11 par exemple qui s'écrit avec deux "1".
Pour 11 j'ai trouvé pour l'instant :
11 = ((log en base 2048 de (racine carré de (racine carré de 16)))^-1)^(3579^(sin pi radian))
(ici j'utilise le fait que 2048 = 2 ^ 11 et que : log en base (2^n) 2 = 1/n).
Mais pour l'instant je n'ai rien qui me permette de générer tous les entiers.
Sinon si je note "ln x" pour "log en base e de x", on a : ln (e^x)^2 = 2x
et donc si je trouve un nombre, alors grâce à cette méthode je peux trouver son double. Donc si j'arrive à générer les nombres impairs, alors j'ai gagné, mais je n'ai pas de piste pour le moment 
Ou alors il faudrait arriver à "coder" l'opération "+1", mais pour l'instant je ne vois pas comment accomplir ce miracle ^^.
Il y a sûrement plus simple.
#8 - 11-12-2014 19:15:57
- cogito
- Expert de Prise2Tete
- Enigmes résolues : 48
- Messages : 593
petit exzrcice (i)
ça y ait 
j'ai accompli mon miracle 
On a pour tout x, ln (e*e^x) = x+1.
de plus pour tout y, ln (y^a) = a* ln y.
Donc si je prend a = e et y = e^(e^x) alors ln (y^e) = e* ln y = e*e^x.
Et donc cela signifie que ln (ln ((e^(e^x))^e)) = x+1.
Donc j'ai 0 (0 ^ 123456789) et j'ai l'opération "+1" donc je peux ainsi générer tous les entiers en itérant à partir de 0 l'opération "+1" autant de fois que nécessaire.
Il y a sûrement plus simple.
#9 - 12-12-2014 09:32:58
- unecoudée
- Professionnel de Prise2Tete
- Enigmes résolues : 0
- Messages : 319
petit exercixe (i)
salut.
cogito , je reconnais que ta résolution fonctionne à merveille avec la fonction "ans"
de la calculette
en effet , si tu tapes 0^123456789 return te donne 0 qui se mémorise dans "ans" st ensuite tu rentres ta formule en remplaçant x par "ans" , tu génères bien tous les nombres .
moi , je n'utilise pas la fonction "ans" j'ai une écriture plus simple à laquelle j'ajoute un seul symbole mathématique pour passer de n à n+1
il y a donc n fois le même symbole pour définir n
merci de vous être pris la tête . je vous laisse encore chercher un peu, et je ne vais pas tarder à mettre momentanément une solution cachée
#10 - 12-12-2014 11:56:01
- cogito
- Expert de Prise2Tete
- Enigmes résolues : 48
- Messages : 593
petit exercicr (i)
Non, je n'ai pas besoins de la fonction "ans" :
par exemple :
3 = (ln (ln ((e^(e^(ln (ln ((e^(e^(ln (ln ((e^(e^(0^123456789))^e)))))^e)))))^e)))
Pour faire plus simple si je note 0 pour 0^123456789 et S(x) = ln (ln ((e^(e^x))^e)) alors j'ai :
n = S(S(S...(S(0)))...) où la fonction S est utilisée n fois.
après certes, mon expression est sans doutes un peu compliquée, et longue à taper, mais j'ai souvent du mal à faire dans la simplicité 
En fait, ici on utilise la construction de Peano des entiers.
Un entier est soit 0, soit le successeur d'un entier. C'est une définition récursive des entiers. La fonction "successeur" est souvent notée "S" ainsi les entiers sont représentés successivement :
0, S(0), S(S(0)), ... pour 0,1,2,...
Pourtant j'ai passé beaucoup de temps à jouer avec ma calculatrice dans ma jeunesse ^^, mais je n'arrive pas à me rappeler un symbole qui permettrait de jouer le rôle de la fonction successeur 
Il y a sûrement plus simple.
#11 - 12-12-2014 12:03:21
- unecoudée
- Professionnel de Prise2Tete
- Enigmes résolues : 0
- Messages : 319
Petit exercice (II)
Spoiler : le début de solution caché
1 = logarithme en base 2 du logarithme en base b de c
2 et b sont les bases des 2 log et c , l'argument .
déterminer 2 , b & c en utilisant une fois 0,1,2,3,4,5,6,7,8,9
#12 - 13-12-2014 14:46:43
- cogito
- Expert de Prise2Tete
- Enigmes résolues : 48
- Messages : 593
petit exercice (u)
En gros on cherche b et c tel que b^2 = c, on peut prendre par exemple :
b = 3^1 et c = 9^(45678^0)
Il y a sûrement plus simple.
#13 - 13-12-2014 18:13:56
- unecoudée
- Professionnel de Prise2Tete
- Enigmes résolues : 0
- Messages : 319
Peti exercice (I)
salut.
cogito. il faut pouvoir exprimer tout nombre entier avec une itération.
l'itération est dans la base b.
#14 - 13-12-2014 21:11:28
- cogito
- Expert de Prise2Tete
- Enigmes résolues : 48
- Messages : 593
Petit xercice (I)
D'accord, pour avoir 2 il faut que la nouvelle base b' après "itération" soit tel que b'^4=c <-> b'^4=b^2 <-> b'=racine de b
donc en rajoutant des racines carrés devant b autant de fois que nécessaire, tu peut atteindre n'importe quel entier.
EDIT : Je pense qu'on pourrait aussi bien élever au carré c autant de fois que nécessaire, ça reviendrait au même.
Les deux solutions ont en commun l'idée que la fonction logarithme transforme les puissances en multiplications et les multiplications en additions, donc en utilisant l'opération "puissance" (EDIT : si on considère la racine carré comme une puissance 1/2) et le logarithme deux fois on peut obtenir une addition. il faut ensuite trouver les bonnes valeurs pour les bases et les arguments pour obtenir l'opération "+1".
Merci pour ce petit problème 
Il y a sûrement plus simple.
#15 - 14-12-2014 00:56:59
- unecoudée
- Professionnel de Prise2Tete
- Enigmes résolues : 0
- Messages : 319
Petit exercice (I
salut.
ma réponse :
logarithme en base (cos 2460°)^(e^(i.pi)) du logarithme en base racine carrée de (9^7) de 81 ^ 3.5 = 1
logarithme en base (cos 2460°)^(e^(i.pi)) du logarithme en base racine carrée de la racine carrée de (9^7) de (81 ^ 3.5 ) = 2 etc..
n radicaux enchevêtrés pour n
premier log base 2 = ( cos 2460°)^-1 = 0.5^-1
l'argument du premier log est le second log en base sqrt(9^7)
l'argument du second log est 81^3.5
je reviendrai dessus lorsque latex sera revenu.
#16 - 14-12-2014 11:29:14
- cogito
- Expert de Prise2Tete
- Enigmes résolues : 48
- Messages : 593
Petit exerrcice (I)
Dans i.pi il y a une multiplication ?!?
Il y a sûrement plus simple.
#17 - 15-12-2014 01:37:47
- unecoudée
- Professionnel de Prise2Tete
- Enigmes résolues : 0
- Messages : 319
petit exercicr (i)
cogito.
effectivement mais je pouvais tout aussi bien remplacer par la fonction inverse 1/x
qui elle était acceptée dans l'énoncé avec x² .
cette dernière m'est venue à l'idée et j'ai effectivement zappé le produit dans l'exposant.
donc on dira (cos2460)^-1 pour la base 2
merci d'avoir fait la remarque.
Mots clés des moteurs de recherche
|
 |

 Accueil
Accueil
 Forum
Forum






