|
#1 - 29-12-2014 12:49:58
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3839
ub si long chemin ???
Bonjour à tous.
2 droites sécantes, un point A situé à une unité du point de croisement. Le point A se déplace jusqu'à l'autre droite par le trajet le plus court, puis revient sur la droite origine également par le trajet le plus court et ainsi de suite jusqu'à ce qu'on atteigne le point de croisement. Il a été dit que la distance totale parcourue mesure 1 milliard d'unités. Est ce possible et si oui dans quelle condition ?
Bonne recherche.
#2 - 29-12-2014 13:04:08
- Promath-
- Elite de Prise2Tete
- Enigmes résolues : 18
- Messages : 1416
- Lieu: Au fond de l'univers
un di long chemin ???
Les droites se situent sur un plan incurvé? Du genre non euclidien?
Un promath- actif dans un forum actif
#3 - 29-12-2014 13:33:50
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3839
Un si long chemin ????
On est dans le plan euclidien classique.
#4 - 29-12-2014 15:14:23
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 6,194E+3
#5 - 29-12-2014 17:11:40
- Jackv
- Elite de Prise2Tete
- Enigmes résolues : 34
- Messages : 3615
- Lieu: 94110
Un si long chemin ??
Première idée, rapide, sans trop réfléchir :
l'Arctg entre les deux droites ne serait-il pas loin de valoir 10^-9  ? ?
#6 - 29-12-2014 17:26:06
- NickoGecko
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 1823
Un si olng chemin ???
Il aurait pu pleuvoir, con comme il est ! (Coluche)
#7 - 29-12-2014 17:30:41
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3839
un di long chemin ???
@Gwen: ce paradoxe, réel, est bien souvent éludé par les mathématiciens, en fait. Je partage ta perplexité, mais je ne rentre pas dans une longue théorie qui ferait polémique.
@JackV et Gwen: vous ne voulez pas calculer la longueur du trajet réel ?
Sinon, c'est à peu près ça, sauf pour JackV qui a un problème de simple au double, ce qui n'est tout de même pas mal.
#8 - 29-12-2014 17:37:34
- Promath-
- Elite de Prise2Tete
- Enigmes résolues : 18
- Messages : 1416
- Lieu: Au fond de l'univers
un si long chrmin ???
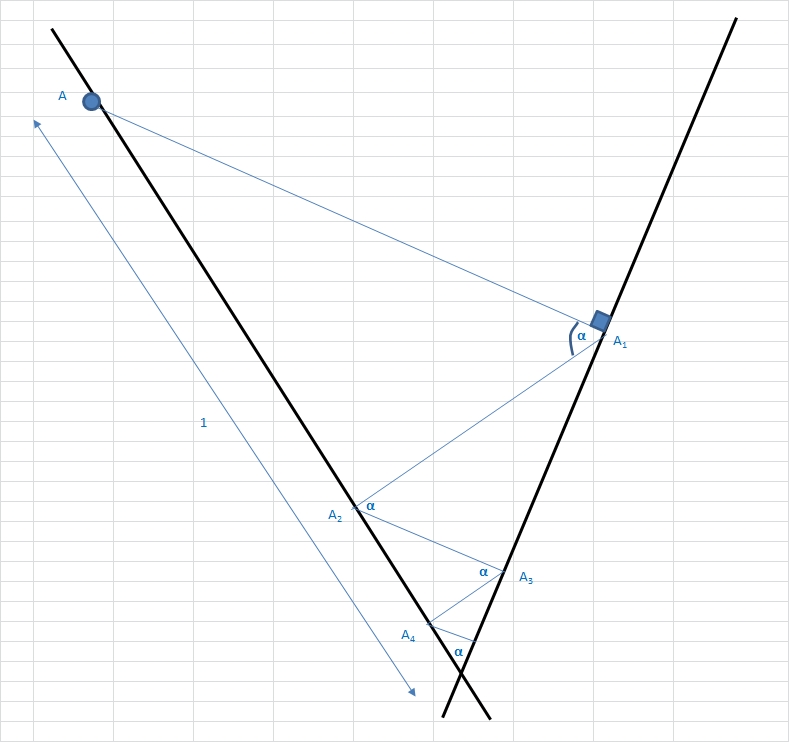
On note [latex]A_1[/latex] et [latex]A_2[/latex] les deux premiers points de touche après A. On obtient finalement une suite de segments dont la longueur décroît toujours du même facteur k. On obtient ainsi la somme des termes d'une suite géométrique.
Cherchons a. On note alpha l'angle aigu délimité par les droites (qui existe car les droites ne peuvent être perpendiculaires). On trouve que celui-ci est égal au sinus de alpha. Ainsi a=sin(alpha)
Cherchons k. k=A1A2/AA1=sin(alpha)/tan(alpha)=cos(alpha)
La somme des termes de la suite représentée par U_n=A_nA_(n+1) est égale à ak^0+ak^1...+ak^n=a(k^(n+1)-1)/(k-1)
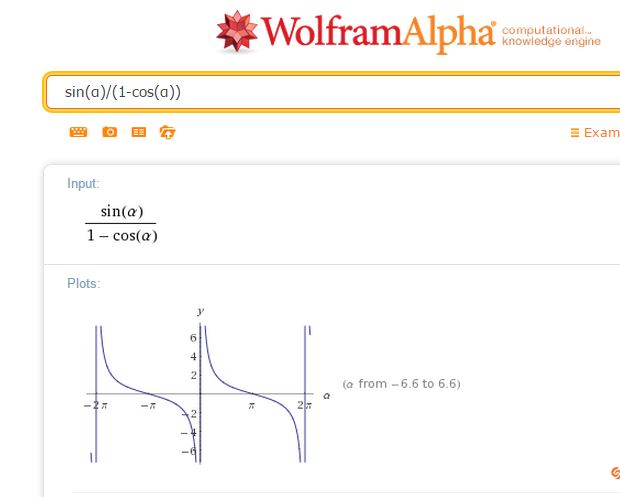
Or, n tend vers l'infini, car on finit par rejoindre le croisement des droites, donc la somme égale a/(1-k)=sin(alpha)/(1-cos(alpha))=(1+cos(alpha)/(sin(alpha))
je note alpha x pour simplifier
=(1+cosx)/(sqrt(1-cos²x)
=10^9 selon l'énoncé
ainsi
(1+2cosx+cos²x)/(1-cos²x)=10^18
1+2cosx+cos²x=10^18-10^18cos²x
(1+10^18)cos²x+2cosx+(1-10^18)=0
Une équation simpliste pour wolfram
or cos(x)>0 donc cosx=(10^18-1)/(1^18+1)
L'angle délimitant les deux droites est ainsi égal à 1,9999999999999999993333333333333333337*10^(-9) radians, ce qui est très petit je crois
Un promath- actif dans un forum actif
#9 - 29-12-2014 17:37:50
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3839
Un si lon gchemin ???
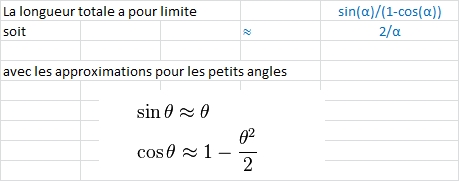
@Nicko: t'es sûr que AA1= tg a ? Pour moi, la tg est le rapport entre le coté opposé et le coté adjacent. Mais ça fait bien longtemps que je n'ai plus fait de trigo. Sinon, pour le reste c'est aussi ma démarche. Pour les très petits angles, il y a des assimilations qu'on peut utiliser.
#10 - 29-12-2014 17:40:20
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3839
un su long chemin ???
Promath, c'est Ok, bravo !
Pour la valeur, je ne me suis pas servi de wolfram et je ne suis pas tombé loin du tout....
#11 - 29-12-2014 18:23:28
- Franky1103
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 3238
- Lieu: Luxembourg
Un si long chmin ???
Soit A l’angle entre les deux droites. Soient ai et bi respectivement les i-èmes trajets entre les deux droites et les i-èmes projections de ces trajets sur la droite d’origine.
On a: ai = a0.(cosA)^i; et: bi = a0.(sinA)^i; ce qui donne:
Som(ai) = a0.[1–(cosA)^n] / [1–cosA]; et: Som(bi) = a0.[1–(sinA)^n] / [1–sinA]
et donc: lim(n->+oo) Som(ai) = 10^9 = a0/(1–cosA)
et aussi: lim(n->+oo) Som(bi) = 1 = a0/(1–sinA)
d’où: (1–sinA)/(1–cosA) = 10^9
soit: (2.10^9–1).t² + 2t – 1 = 0, en posant: t = tan(A/2)
On trouve: tan(A/2) = env. V5.10^(-5); soit: A = env. 2V5.10^(-5) radian
Il est vraiment étonnant que la valeur de l'angle entre les deux droites permette d'obtenir n'importe quelle valeur de la distance totale parcourue.
#12 - 29-12-2014 18:40:33
- NickoGecko
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 1823
un si long chemun ???
argh, une erreur de débutant au début, corrigée dans le post initial en principe ...
merci !
Il aurait pu pleuvoir, con comme il est ! (Coluche)
#13 - 29-12-2014 18:45:15
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3839
Un si long cchemin ???
Francky, je partage totalement ton étonnement pour la possibilité d'obtenir un trajet aussi long. Sinon, revois tes calculs, il y a un souci dès le début je crois, avec les ai et les bi.
#14 - 29-12-2014 18:52:20
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3839
in si long chemin ???
NickoGecko, tu n'as pas repris la valeur de AA1 , qui n'est pas tg a.
#15 - 29-12-2014 18:56:51
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3839
un si lobg chemin ???
@ Gwen: pour l'instant, je n'ai pas compris ta formule cosa+1=10^9 sina. ça me semble intéressant pourtant, étant donné le résultat proche de la réalité. Pourrais tu détailler un peu ?
#16 - 29-12-2014 19:33:36
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 6,194E+3
Un si lonng chemin ???
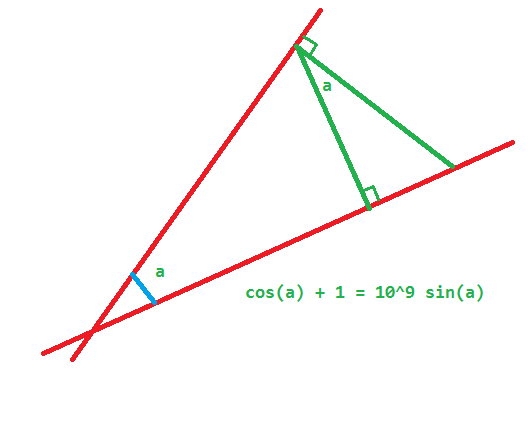
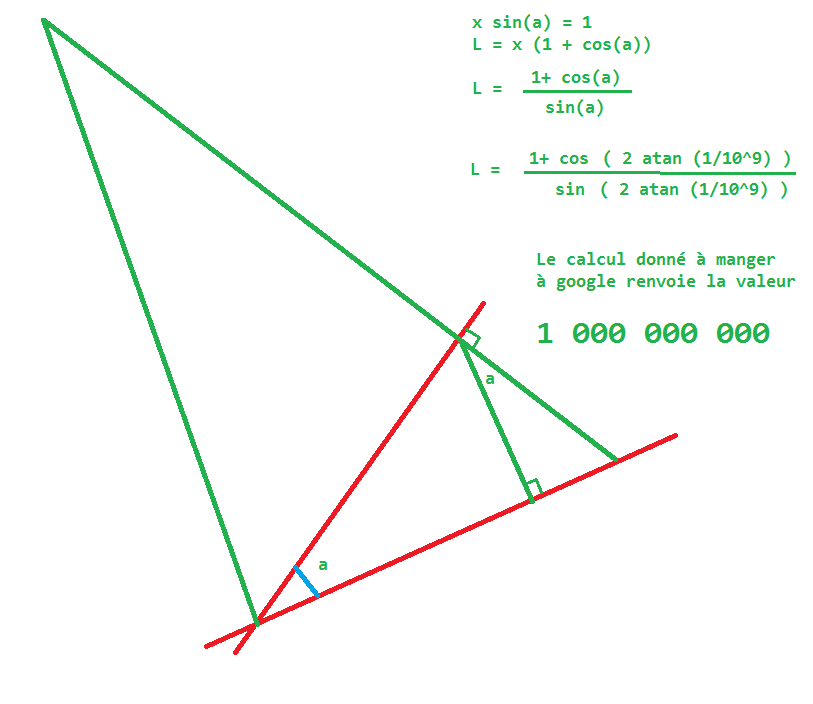
La distance parcourue le long de la première droite sera de 1 au final.
Sur l'aller-retour que j'ai illustré en vert , je considère juste le rapport entre l'aller-retour vert et la distance parcourue le long de la droite rouge.
Autrement dit 1 + cos a par rapport à sin a (quelle que soit l'échelle)
Vu qu'on aura sur tout le trajet une succession de triangles homothétiques, ce rapport ne variera pas d'un chouilla. Donc si je fixe ce rapport à 10^9 pour un aller retour, il sera consant le temps d'avancer de 1 le long de la droite rouge et d'atteindre le point d'intersection.
On aura parcouru 10^9 unités si (1+cos a) / sin a = 10^9
Mais je ne comprends pas ta question... le trajet réel fait 10^9. Ta question est de savoir si on peut le faire et dans quelles conditions. Oui on peut le faire  Après, la formule obtenue est une approximation, mais ce n'est plus la même question. Après, la formule obtenue est une approximation, mais ce n'est plus la même question.
#17 - 30-12-2014 00:17:21
- Franky1103
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 3238
- Lieu: Luxembourg
un si long chemun ???
Je me suis en effet emmêlé les crayons, car seuls les "bi" pairs sont concernés.
On a toujours: lim(n->+oo) Som(ai) = 10^9 = a0 / (1–cosA); et Som(bi pairs) = 1
Or: sinA = a0 / Som(bi pairs); donc: sinA = a0; d’où: sinA / (1–cosA) = 10^9
soit: tan(A/2) = 1/10^9 = 10^(-9); et enfin: A = env. 2.10^(-9) radian
En généralisant, pour D "assez grand", on aura: A = env. 2/D radian
Je continue bien sûr d'être étonné: plus on ferme l'angle A et plus D devient grand (l'augmentation du nombre de trajets l'emporte sur la dimension de ces trajets).
#18 - 30-12-2014 09:30:46
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3839
Un si long chein ???
Francky c'est tout bon.
Pour améliorer l'intuition de cet algorithme, on peut s'y prendre d'une façon légèrment différente et on comprend tout de suite ce qu'il se passe. J'en parlerai dans ma réponse.
#19 - 30-12-2014 09:55:43
- unecoudée
- Professionnel de Prise2Tete
- Enigmes résolues : 0
- Messages : 319
Un si long chemin ??
salut.
OA = 1 , A étant sur une des droites
premier chemin :a = sinB
second chemin : b = sinB.cosB
troisième chemin:c = sinB.cos²B.....
Par conséquent , si je pose cosB = X et sachant que je n'arriverai jamais en O , la distance maximum est réalisée en faisant le maximum de navettes entre les 2 droites. j'appelle n le nombre de navettes
et d = sqrt(1-X²) . (X^n - 1)/(X-1)
cette distance , je n'ai pas pu la faire évoluer au delà de :10000000 X V2
soit: 14142135,6237.. unités avec cosB = 0.99999999999999999...
et n = 10000000000000000.. .
quand au milliard d'unités , je ne sais pas faire.
#20 - 30-12-2014 10:33:00
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3839
in si long chemin ???
Gwen, c'est OK pour ta démarche originale. Dans le corrigé, tu verras qu'on peut vite arriver au résultat sans aucune manip de trigo, mais juste en se servant des assimilations pour les petits angles.
A unecoudée, ton départ est bon, mais il est impossible de compter le nombre d'aller-retour: il est infini !
#21 - 30-12-2014 10:36:27
- unecoudée
- Professionnel de Prise2Tete
- Enigmes résolues : 0
- Messages : 319
un qi long chemin ???
@nodgim. mais je sais qu'il est infini . mais je trouve une limite avec d . puisque j'ai précisé en amont que je n'arriverai jamais en O.
#22 - 30-12-2014 13:07:43
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3839
un si long chemun ???
@une coudée: pour ton X^n, avec X<1, et quand n----->inf, c'est zéro.
Si ça peut t'aider...
#23 - 30-12-2014 15:05:41
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
Un si long chemin ??
Je n'ai pas trop cherché mais il me semble que le trajet est de longueur 1/tan(â)+1/sin(â) . Après il suffit de choisir l'angle â comme il faut ...
Vasimolo
#24 - 30-12-2014 17:10:50
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3839
Un si long chemin ??
Intéressant Vasimolo. Si tu pouvais développer...
#25 - 30-12-2014 17:41:11
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
Un si long chemin ??
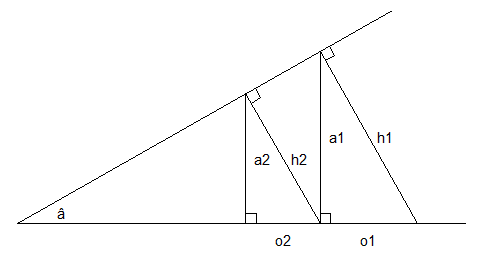
C'est de la trigo de base : ai=oi/tan(â) et hi=oi/sin(â) .
Comme la somme des oi vaut 1 la somme des ai+hi vaut 1/tan(â)+1/sin(â) .
Vasimolo
|
 |

 Accueil
Accueil
 Forum
Forum