Forum dédié aux énigmes et à toutes formes de jeux de logique. | Déconnexion |
|
Tu n'es pas identifié sur Prise2tete : s'identifier.  Accueil Accueil
 Forum Forum
|
 |
#26 - 13-05-2015 08:52:37#0 Pub#27 - 13-05-2015 12:54:17#28 - 13-05-2015 13:40:05#29 - 13-05-2015 18:30:04#30 - 13-05-2015 18:48:08
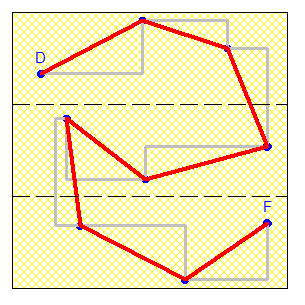
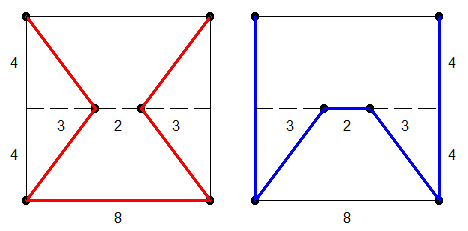
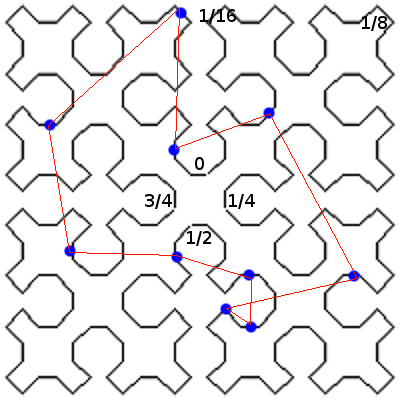
âGteau 98C'est aussi ma solution Vasimolo. Je n'ai pas pu trouver une autre config qui donnerait un chemin plus long, mais je ne prouve pas non plus que ça n'existe pas. Une certitude toutefois: les 4 pts aux sommets du carré. #31 - 14-05-2015 01:32:01
gâyeau 98Tout d'abord merci à Vasimolo pour son appétissant gâteau, le sujet est très intéressant. #32 - 14-05-2015 11:23:59#33 - 14-05-2015 12:47:30
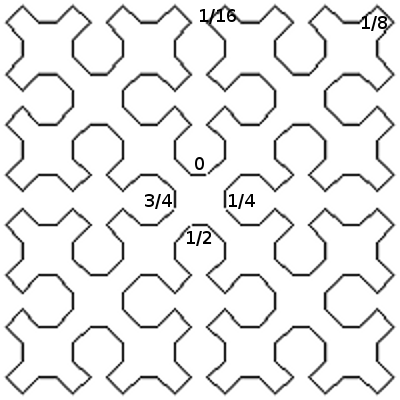
Gâteu 98La construction de la courbe est illustrée ici : #34 - 14-05-2015 18:45:24#35 - 14-05-2015 22:31:31
gâteai 98S'il est vrai que la courbe de Sierpinski est tordue, elle ne sert qu'à déterminer l'ordre dans lequel les points seront visités. La ligne brisée obtenue n'est elle pas si tordue que ça, cf la 3e illustration. #36 - 14-05-2015 23:35:06
Gâtea u98Si on prend un point au hasard et qu'on visite successivement le point le plus proche non déjà visité, on doit arriver sur un bon score. Mais où est la preuve? Un promath- actif dans un forum actif Réponse rapideSujets similaires
|
 | |||||||||||||||||||||||||||||||||
| Prise2Tete Forum Statistiques Liste des membres Hall of Fame Contact | |||||||||||||||||||||||||||||||||||
Un jeu où seules la réflexion, la logique et la déduction permettent de trouver la solution.