|
#1 - 07-05-2015 12:48:45
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
gâteay 98
Bonjour à tous 
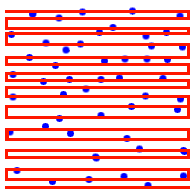
La dernière création de mon pâtissier : un gâteau carré de 20 cm de côté recouvert d’une couche de crème et piqué de 49 myrtilles .
Pour appâter le client il lie les graines d'un chemin en coulis de fraises .
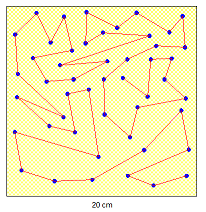
Le chemin de fraises est simple ( pas de point double ) .
Il prétend pouvoir réaliser un coulis de moins de 10 m de long quelle que soit la disposition des myrtilles .
L’affirmation semble raisonnable mais comment démontrer un truc pareil ?????
Vasimolo
PS : ceux qui trouvent que 10 m est excessif peuvent essayer d’améliorer le résultat .
#2 - 07-05-2015 18:30:51
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3839
Gââteau 98
Pour être sûr de comprendre la question: le chemin de coulis est il fait au hasard (dont le plus long est possible) ou optimisé (au plus court) ?
#3 - 07-05-2015 18:34:52
- Promath-
- Elite de Prise2Tete
- Enigmes résolues : 18
- Messages : 1416
- Lieu: Au fond de l'univers
fâteau 98
Facile, on les relies de gauche à droite, et selon l'inégalité triangulaire la liaison n aura une longueur L(n)<Delta(x)+Delta(y) où Delat(x,y) sont les longueurs en x et y du coulis
Ainsi Sigma(i,L(i))<0.2+48*0.2 (respectivement la variation totale en x maximale et la variation totale en y maximale) donc la longueur totale du coulis L<9.8
On aurait pu mettre 50 myrtilles sans perdre la propriété L<10 
Un promath- actif dans un forum actif
#4 - 07-05-2015 18:42:58
- Ebichu
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 888
#5 - 07-05-2015 18:46:58
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
âteau 98
@Nodgim : le pâtissier essaie d'économiser le coulis , il ne relie relie donc pas les points au hasard .
@Promath : bien vu , tu tentes 3 m de coulis ???
Vasimolo
#6 - 07-05-2015 18:47:53
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3839
gâtezu 98
Depuis chaque sommet, on trace un arc de cercle de rayon 20 cm. ça partage le carré en 9 zones. Entre 2 pts extrêmes de chacune de ces zones il y a moins de 20cm. Entre 2 zones voisines il y a moins de 20 cm. Comme il y a 48 segments entre les 49 pts, La distance totale est <48*20 cm=9m60.
Le plus intéressant serait de calculer la plus longue distance minimale. Mais c'est autrement plus compliqué.
#7 - 07-05-2015 19:21:08
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
#8 - 07-05-2015 19:33:21
- Promath-
- Elite de Prise2Tete
- Enigmes résolues : 18
- Messages : 1416
- Lieu: Au fond de l'univers
hâteau 98
On découpe le carré en n bandes. Il y a 49 myrtilles sur ces n bandes. On les parcourt ainsi de gauche à droite, puis on descend d'une bande que l'on parcourt de droite à gauche, puis on descend, de gauche à droite et on obtient un serpent en descendant. Le parcours en x sera au maximum de 20n. Le parcours en y sera de 20/n*48 auquel il faut ajouter n sauts (de longueur 20/n supplémentaire) entre deux bandes ce qui fait une longueur totale de 20n+980/n. Une telle "fonction" admet un minimum en 7, avec une longueur totale inférieure à 2.80, ce qui améliore franchement le résultat! Je travaille sur des congruences sur les bandes pour le diminuer encore.
Amélioration du résultat: pour un tel nombre de bandes (8)
On considère une bande quelconque. Si on la parcourt de droite à gauche alors le pire des cas sera celui où on traversera intégralement la diagonale d'un coup pour faire des alternances ensuite haut-bas. On traversera donc 8 diagonales (car 8 bandes) puis on fera au pire des haut-bas. On peut donc réduire la distance finale en ajoutant les 8 diagonales puis en soustrayant les 8 variations en x et en y des diagonales, remplacées par leur variation réelle. Cela donne 2.80-1.6-0.2+8sqrt(0.040625) (la valeur d'une diagonale de bande)
soit 2.8-0.19 donc 2.61
Un promath- actif dans un forum actif
#9 - 08-05-2015 01:07:37
- Ebichu
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 888
Gâteaau 98
3 m de coulis ? J'ai mieux !
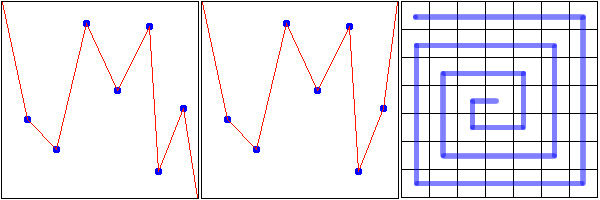
Commençons par décrire une méthode de parcours d'un carré.
A l'intérieur d'un carré de côté 1, on étale le coulis en joignant les myrtilles par une ligne brisée se déplaçant obligatoirement de gauche à droite (éventuellement sur la même verticale). De plus, on impose que le coulis parte d'un coin, et termine sur le coin opposé (type A, voir figure de gauche), ou à l'autre extrémité du même côté (type B, voir figure du milieu).
Alors s'il y a m myrtilles dans le carré, on peut montrer (je peux détailler si nécessaire) que la longueur du coulis est majorée par :
* m+1 si m est pair et qu'on impose le type B, ou si m est impair et qu'on impose le type A.
* m+1 + (racine(2)-1) si m est pair et qu'on impose le type A, ou si m est impair et qu'on impose le type B (NB : oui, je sais, ça fait m+racine(2), c'est pour simplifier le propos plus loin).
Revenons maintenant à notre gâteau, qu'on découpe en 7x7 cellules carrées. On va parcourir ces 49 cellules en spirale (voir figure de droite). Dans chaque cellule, on appliquera la méthode précédente, et on va se débrouiller pour que les chemins de ces cellules se recollent.
En partant du début de la spirale, chaque cellule sera du type A ou B, peu importe (on choisit donc le moins coûteux), sauf pour les 12 cellules où la spirale fait un angle droit : il peut alors être nécessaire d'imposer une cellule de type B, pour que le recollement s'opère.
On obtient ainsi un chemin dont la longueur totale est (49+49+12(racine(2)-1))*20/7. Explications :
* 20/7 est le côté des cellules.
* On somme (m+1) sur les 49 cellules : somme(m)=49 car il y a 49 myrtilles en tout, et somme(1)=49.
* Les 12 cellules avec l'angle droit risquent de se voir imposer un surcoût de (racine(2)-1), d'où ce dernier terme.
Au final, on trouve 1720/7 + 240.racine(2)/7, soit environ... 294 cm 
#10 - 08-05-2015 09:09:08
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
Gâtea u98
Les résultats commencent à s'affiner 
Promath propose deux méthodes ou plutôt une méthode et une variante .
Résultat 2,80 m pour la première et 2,61 m pour la variante .
Ebichu a pris un autre chemin il arrive à 2,94 m .
Peut-on faire encore mieux ?
Vasimolo
#11 - 08-05-2015 11:47:06
- Ebichu
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 888
Gâteau 9
2,61 m ? Woh, les producteurs de fraises ont du souci à se faire.
Jusqu'à quel point ? En plaçant les myrtilles sur un réseau à mailles carrées de côté 20/6 cm, il faudra au moins 20/6*48 = 160 cm de coulis.
L'étau se resserre 
#12 - 08-05-2015 12:21:09
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
#13 - 08-05-2015 14:28:29
- Promath-
- Elite de Prise2Tete
- Enigmes résolues : 18
- Messages : 1416
- Lieu: Au fond de l'univers
Gâtaeu 98
Un petit quadrillage de 6.6 avec les myrtilles aux extrémités devrait suffir pour 1.60 minimum de parcours
D'ailleurs je n'ai pas mieux qu'ebichu, j'ai fait un calcul erroné il me semble, j'ai 2.94 en le refaisant... Ex aequo donc!
Un promath- actif dans un forum actif
#14 - 08-05-2015 16:01:22
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
gâtrau 98
@Promath : tu pourrais détailler ton calcul , c'est assez difficile de décrypter à demi-mot 
Vasimolo
#15 - 08-05-2015 18:23:31
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3839
fâteau 98
Je n'ai pas approfondi, mais je suppose que les 3 métres et moins viennent d'un découpage du carré en 49 petits carrés. ça me semble un peu compliqué, mais y a peut être une piste meilleure avec des hexagones.
#16 - 08-05-2015 18:40:00
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
Gââteau 98
Les petits carrés c'est aussi l'idée d'Ebichu , de simples bandes pour Promath et moi-même . Je ne sais rien de la borne inférieure de la longueur de coulis à part qu'elle est inférieure à 3 m : le problème est sûrement ouvert .
Il est aussi amusant de chercher les positions des graines qui vont forcer le pâtissier à répandre au maximum son précieux coulis 
Vasimolo
#17 - 09-05-2015 10:34:40
- Promath-
- Elite de Prise2Tete
- Enigmes résolues : 18
- Messages : 1416
- Lieu: Au fond de l'univers
Gâteau 9
Pour 7 bandes, le cas le pire, où le parcours est le plus long comme évoqué pus haut est le cas où iles bandes sont traversées en 1 fois d'un coup en diagonale, puis par une alternance de haut bas.
La variation sur l'axe x est de 0.2*7-0.2*7 (diagonales)
La variation sur l'axe y est de 48*0.2/7 (le nombre d'alternances haut-bas) -7*0.2/7 (diagonales)+6*0.2/7 (sauts entre deux bandes)
Il ne faut pas oublier d'ajouter les diagonales de longueur sqrt(0.2²+0.2²/7²)
Au total cela fait sqrt(2)+47/35 soit environ 2.76!
Un promath- actif dans un forum actif
#18 - 09-05-2015 11:14:59
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
#19 - 09-05-2015 12:55:07
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3839
Gâeau 98
Sans pouvoir le prouver, je conjecture que le max tournerait plutôt vers les 2 mètres (en mettant les pts aux sommets de triangles équilatéraux presque tous isométriques).
#20 - 09-05-2015 13:13:18
- Promath-
- Elite de Prise2Tete
- Enigmes résolues : 18
- Messages : 1416
- Lieu: Au fond de l'univers
âteau 98
Pour fixer une borne inférieure à la borne inférieure (donc pour contraindre notre pâtissier à utiliser le plus de coulis, on quadrille avec des myrtilles sur 7*7 de sorte à ce que la distance minimale d'une myrtille à une autre soit de 0.2/6 (7*7 myrtilles qui définissent 6*6 carreaux). Ainsi le chemin le plus court sera de 48*0.2/6 soit de 1,6, on ne peut pas descendre en dessous de cette longueur (mais on peut éventuellement monter, je travaille sur une quinquonce)
Un promath- actif dans un forum actif
#21 - 09-05-2015 13:13:47
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
Gtâeau 98
Ebichu a montré que 1,60 m est une fourchette basse mais on doit pouvoir faire pire 
Vasimolo
#22 - 09-05-2015 13:35:59
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3839
Gâetau 98
Ah ben oui ce 1m60 c'est quand on met les pts aux sommets d'un quadrillage carré. Dans ce cas, on peut bouger les pts jusqu'à une certaine limite (c'est là qu'intervient le triangle équilatéral) et allonger le chemin, sans pouvoir trouver un autre cheminement plus court. Car c'est bien là tout le problème: déplacer les pts pour allonger le chemin, mais pas trop sinon on va trouver un autre chemin plus court.
#23 - 09-05-2015 15:15:02
- Promath-
- Elite de Prise2Tete
- Enigmes résolues : 18
- Messages : 1416
- Lieu: Au fond de l'univers
hâteau 98
Après réflexion, je n'ai pas pu faire pire que 1.60 car tout déplacement induit soit rien, soit une diminution de cette longueur d'après Pythagore...
Un promath- actif dans un forum actif
#24 - 10-05-2015 12:58:12
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
Gâteau 9
Je crois que l'on ne fera pas beaucoup mieux que le résultat donné par la stratégie de Promath . Il est d'ailleurs assez curieux de constater qu'une méthode aussi simple fournisse un tel résultat .
Une illustration avec 3 bandes au lieu de 7 :
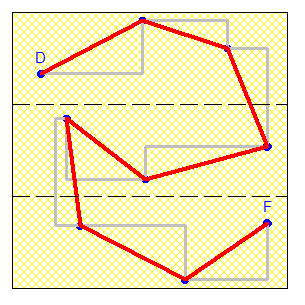
Trouver une meilleure stratégie devient vite un énorme casse-tête même si on explose le record avec n'importe quel exemple que j’ai pu essayer .
Un grand merci aux participants 
Vasimolo
#25 - 10-05-2015 18:05:36
- Promath-
- Elite de Prise2Tete
- Enigmes résolues : 18
- Messages : 1416
- Lieu: Au fond de l'univers
Gââteau 98
Un promath- actif dans un forum actif
|
 |

 Accueil
Accueil
 Forum
Forum