20 cm

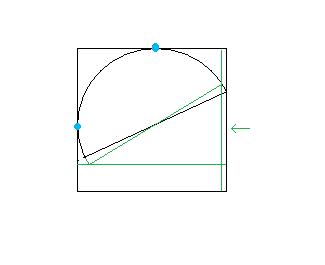
En partant d'un demi cercle de rayon a, on obtient un carré dont le côté vaut [latex]a+\frac{a sqrt{2}}{2}[/latex]

En résolvant [latex]a+\frac{a sqrt{2}}{2}=20[/latex]

On a [latex]a=20(2-sqrt{2})[/latex]

Je suis parti du principe que ton dessin illustrait la situation optimale

...

Le dessin de Vasimolo est le seul cas où le carré est deux fois tangent au gâteau (hormis le cas où le côté du carré et le diamètre du gâteau sont confondus mais qui offre un rayon plus petit), ceci semble lui assurer la solution optimale.

Mais ce n'est pas un preuve

Parce que la part se trouve dans un carré !

Si la part est dans une autre orientation, alors on peut la tourner (en gardant les deux contacts cercle-carré [en bleu sur le dessin]), comme ci-dessous (nouvelle part qu'on a tournée en vert):



à ce moment, la part ne toucherait plus deux bords (en bas et à droite : en particulier elle ne toucherait plus à droite), et on pourrait la faire plus grosse.

La seule configuration ou on ne peut pas la faire tourner (et donc grossir) est quand la part est disposée à 45°, qui est par conséquent optimal.

Bonne réponse de pierrot13 , Mcflambi et lesingemalicieux

Même si c'est intuitif , il n'est pas facile d'expliquer pourquoi l'angle de 45° est optimal . On peut supposer comme Mcflambi que le demi-cercle est en contact avec deux bords consécutifs du carré et la rotation de la part autour du centre du cercle donne un carré minimal pour un angle de 45° .

Merci aux participants .

Vasimolo