|
#1 - 07-02-2015 20:05:02
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
#2 - 07-02-2015 20:48:49
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 6,192E+3
gâtezu 92
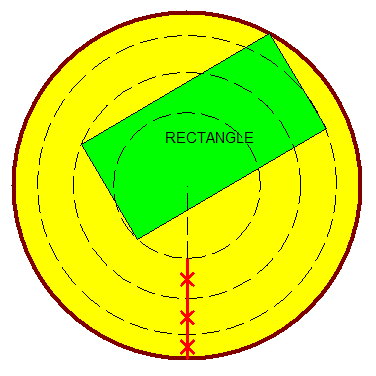
Va falloir des précisions, là ? Il a quoi de spectaculaire le gâteau ? A part de pouvoir coller un rectangle dessus qui touche le bord ...
#3 - 07-02-2015 21:59:05
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
Gâtea 92
Les cercles ont le même centre et selon la coutume, les croix rouges signifient des longueurs égales .
Vasimolo
#4 - 08-02-2015 09:01:02
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3839
Gâeau 92
Il me semble qu'il faut juste poser la pointe du compas quelque part hors les médiatrices et tracer 4 cercles qui passent chacun par un sommet du rectangle.
#5 - 08-02-2015 09:50:50
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 6,192E+3
Gâteua 92
A première vue, je dirais que c'est impossible. sauf si la distance rouge est nulle.
#6 - 08-02-2015 10:14:58
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
hâteau 92
@Nodgim : attention il faut que les segments rouges soient de la même taille .
@Gwen : ton intuition est bonne mais le pâtissier va me demander des justifications 
Vasimolo
#7 - 08-02-2015 10:35:05
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 6,192E+3
Gâteau 29
Ca n'est pas une intuition... 
#8 - 08-02-2015 11:07:12
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
#9 - 08-02-2015 11:16:55
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3839
Gâteeau 92
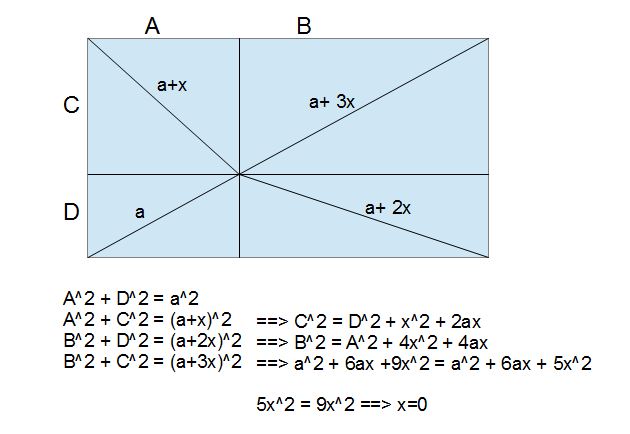
On pose un point dans le plan distant des sommets du rectangle de A, A+x, A+2x, A+3x.
La distance de ce point aux 4 cotés du rectangle est a,b,c,d.
On pose 4 équations de Pythagore
(1) a²+b²=A²
(2) b²+c²=(A+x)²
(3) a²+d²=(A+2x)²
(4) c²+d²=(A+3x)²
(2)-(1)+(3) aboutit à l'équation c²+d²=A²+6Ax+5x²
A comparer avec l'équation (4) qui mène à poser
(A+3x)²=A²+6Ax+5x².
il faut x=0.
On ne peut pas faire un gâteau comme ça.
#10 - 08-02-2015 11:22:36
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
Gâteaau 92
Oui Nodgim 
Vasimolo
#11 - 08-02-2015 11:42:41
- kossi_tg
- Professionnel de Prise2Tete
- Enigmes résolues : 18
- Messages : 307
- Lieu: Montargis
Gâteua 92
Soient (C1), (C2), (C3) et (C4) respectivement les cercles du plus petit au plus grand. Leur centre commun est noté O
Dans un repère orthonormé de centre O (dont on positionnera les axes parallèles aux côtés du rectangles pour simplifier les calculs), les équations des cercles sont:
- (C1): x^2+y^2=r^2
- (C2): x^2+y^2=(r+k)^2
- (C3): x^2+y^2=(r+2*k)^2
- (C4): x^2+y^2=(r+3*k)^2
où r est le rayon de (C1) et k l'écart entre les rayons.
Nommons le rectangle ABCD avec A sur (C1), B sur (C2), C sur (C4) et D sur (C3).
Soient L et l les côtés de ABCD. Si A(a,b) alors B(a,b+l), C(a+L,b+l) et D(a+L,b).
En introduisant les cordonnées de ces points dans les équations de leurs cercles, on a:
* A sur (C1): a^2+b^2=r^2 (1); cette relation sera utilisée pour la suite.
* B sur (C2): l^2 +2*b*l=2*k*r+k^2 (2)
* C sur (C4): L^2+l^2+2*a*L+2*l*b=9*k^2+6*k*r (3)
* D sur (C3): L^2+2*a*L=4*k*r+4*k^2 (4).
En additionnant membre par membre les équations (2) et (4) on a:
(l^2 +2*b*l) + (L^2+2*a*L) = (2*k*r+k^2) + (4*k*r+4*k^2)
soit : L^2+l^2+2*a*L+2*b*l = 6*k*r+5*k^2 (5)
Les membres de gauche des équations (3) et (5) sont égaux donc les membres de droite le sont aussi; soit : 9*k^2+6*k*r = 6*k*r+5*k^2. On en déduit que 9*k^2=5*k^2 donc k=0
La réalisation de ce gâteau est donc impossible sauf d'avoir les 4 cercles de même dimension.
Voilà... sauf si une erreur s'est glissée quelque part 
#12 - 08-02-2015 11:49:08
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
Gâteau 29
Oui Kossi 
On peut faire plus simple en raisonnant directement sur les longueurs sans passer par les coordonnées .
Vasimolo
#13 - 08-02-2015 13:20:56
- Franky1103
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 3238
- Lieu: Luxembourg
Gâtteau 92
Soit ABCD le rectangle centré sur O dans un un repère orthonormé. Les coordonnées des sommets de ce rectangle sont: A(-a;-b); B(-a;+b); C(+a;+b); D(+a;-b) et ceux du centre du cercle concentrique (x0;y0).
A appartient au cercle de rayon R => (a+x0)² + (b+y0)² = R² (1)
B appartient au cercle de rayon R+r => (a+x0)² + (b-y0)² = (R+r)² (2)
C appartient au cercle de rayon R+3r => (a-x0)² + (b-y0)² = (R+3r)² (3)
D appartient au cercle de rayon R+2r => (a-x0)² + (b+y0)² = (R+2r)² (4)
(1) et (2) donnent: -4by0 = r(2R+r); (3) et (4) donnent: -4by0 = r(2R+5r)
d’où: r(2R+r) = r(2R+5r) => r=0
Je trouve donc que les cercles doivent tous avoir le même rayon: c’est étonnant.
#14 - 08-02-2015 18:18:17
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
gâteay 92
Oui Franky 
Vasimolo
#15 - 11-02-2015 18:29:54
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
Gâtau 92
C'était donc impossible 
Pas grand chose à ajouter aux démonstrations déjà produites .
Merci aux participants .
Vasimolo
#16 - 11-02-2015 19:09:10
- Franky1103
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 3238
- Lieu: Luxembourg
GGâteau 92
Ce n'était pas évident car, intuitivement, on peut penser qu'un tel gâteau doit pouvoir se construire. Comme quoi, les intuitions en mathématiques ...
Dans un autre registre, il parait qu'on peut toujours construire un carré dont les quatre sommets appartiennent à une courbe fermée qui ne se croise pas elle-même et qui n'est même pas nécessairement dépourvue de "cassure", mais je crois que ce point a déjà été maintes fois discuté ici.
#17 - 11-02-2015 19:24:30
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 6,192E+3
gâyeau 92
J'ai eu une piste sans calcul que je n'ai pas réussi à suivre... Fausse piste ou pas ?
Si on réduit les distances on arrive à 0 x 2x 3x soit le début d'un genre de spirale c e qui ne peut pas donner de rectangle.
Mais cette réduction se fait depuis le centre des cercles. Depuis le centre du rectangle on est sensé avoir toujours un rectangle. Je n'ai pas réussi à passer de l'un à l'autre ce qui serait un contresens et donc, une impossibilité.
#18 - 11-02-2015 19:29:59
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
Gâtau 92
Le problème du carré de Franky est toujours ouvert à l'heure actuelle .
Vasimolo
|
 |
|
Prise2Tete
Forum
Statistiques
Liste des membres
Hall of Fame
Contact
|

 Accueil
Accueil
 Forum
Forum