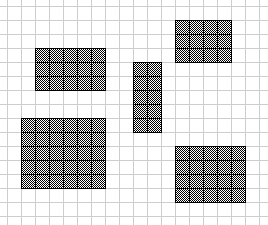|
#1 - 24-02-2016 19:23:47
- Ebichu
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 888
Automatee cellulaire
On définit un automate cellulaire sur un quadrillage à partir des règles suivantes :
* une cellule vivante sera représentée en noir, une cellule morte en blanc.
* initialement, certaines cellules sont vivantes, en nombre fini.
* les cellules sont immortelles : une fois vivantes, elles le restent.
* règle de naissance : une cellule morte ayant au moins 2 voisins vivants parmi ses 4 voisins directs (en haut, en bas, à gauche, à droite, mais pas en diagonale) devient vivante.
Exemple :
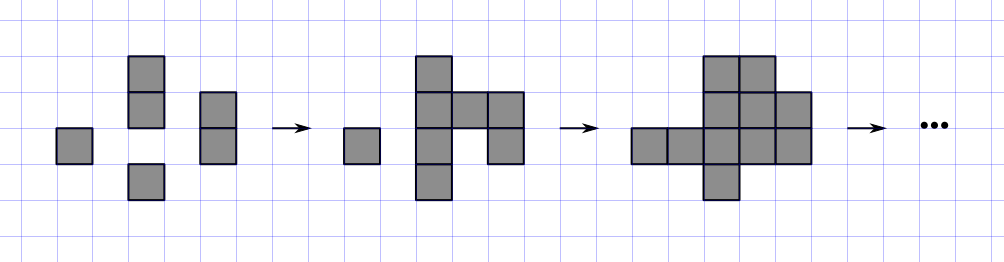
Question 1 - Décrire les états finaux : à quoi ressemble le quadrillage lorsque plus aucune naissance ne se produit ?
Question 2 - Étant donné un état final, quel est le nombre minimal de cellules vivantes dont il faut disposer initialement pour aboutir à cet état ?
Amusez-vous bien !
#2 - 24-02-2016 19:42:56
- dhrm77
- L'exilé
- Enigmes résolues : 49
- Messages : 3004
- Lieu: Fanning Island-?-Lac Tele,Mali
Auttomate cellulaire
1) Quel que soit la grille de depart, le résultat final est toujours une série de rectangles (qui peuvent etre carrés ou meme juste uni-cellulaire, séparé par au moins 2 cases blanches dans toutes les directions.
2) pour un état final d'un rectangle de a*b par example, il suffit de commencer par une série de cellules (1,0,1,0,1,0,1) sur 2 cotés contigus. (0=morte, 1=vivantes):
- a/2 +1 sur un coté
- b/2 +1 sur l'autre
- et -1 parce que le coin est commun.
On peut aussi placer les cellules en diagonale pour commencer et en pointillé pour finir le coté le plus long.
En regle generale on a besoin de int(a+b+1)/2 cellules de depart, pour chaque rectangle final.
Great minds discuss ideas; Average minds discuss events; Small minds discuss people. -Eleanor Roosevelt
#3 - 25-02-2016 01:32:46
- Ebichu
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 888
Automate cellulair
@dhrm77 : 1) Pour que ton résultat soit juste, il faut mieux exprimer la séparation dont tu parles. Dit comme ça, ce n'est pas correct. Et ensuite, il faut encore le démontrer.
2) Je suis d'accord avec ta formule, à condition que tu corriges le parenthésage. Ta disposition prouve que ce nombre est suffisant... mais comment prouver qu'il est nécessaire ?
Bon début, il reste du travail 
#4 - 25-02-2016 08:12:44
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3839
Automate cellulaaire
Salut Ebichu,
Tant que la partie connexe n'est pas convexe, on peut la compléter jusqu'au convexe, c'est à dire un rectangle.
En partant d'une unique cellule, formant un rectangle (L,l)=(1,1) on peut l'agrandir par une cellule disposée à une case blanche de distance, et qui donnera (L+2,l) ou (L,l+2).
Pour obtenir un rectangle impair (L,l) il faudra donc n=(L+1)/2 + (l-1)/2=(L+l)/2 cellules.
Pour un rectangle pair, ajouter 1 cellule.
En fait, on peut disposer les cellules sur le demi périmètre du rectangle à obtenir, de sorte qu'on puisse toujours sauter d'une cellule à la suivante en passant par une seule case blanche (horizontale ou verticale). Ou alors les poser en diagonale.
#5 - 25-02-2016 09:07:56
- masab
- Expert de Prise2Tete
- Enigmes résolues : 44
- Messages : 971
Automate celluulaire
A première vue on peut penser que les états finaux sont des réunions disjointes de rectangles ; 2 rectangles quelconques devant être distants d'au moins 2 cellules mortes.
Voici un exemple
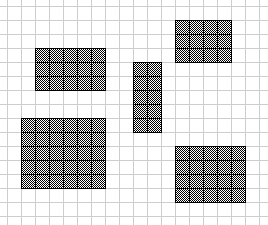
Preuve
Il suffit d'étudier les bords possibles d'un état final.
Ce ne peut être localement que la même chose que pour un rectangle de cellules vivantes.
cqfd
On a supposé qu'au départ il n'y a qu'un nombre fini de cellules vivantes.
L'état final est le plus petit [au sens de l'inclusion] des états finaux du type précédemment indiqué contenant les cellules vivantes de départ.
Il existe : c'est l'intersection de tous les états finaux du type précédemment indiqué contenant les cellules vivantes de départ. Il y en a au moins un : un grand rectangle contenant les cellules vivantes de départ.
Avec un nombre infini de cellules au départ, un état final (il peut ne jamais être atteint...) est composé des cellules vivantes qui sont
soit un quart de plan,
soit un demi-plan,
soit tout le plan,
soit un rectangle dont un côté est parti à l'infini,
soit une bande limitée par 2 droites parallèles.
NB Les bords de tous les états considérés sont composés de segments horizontaux ou verticaux.
#6 - 25-02-2016 12:23:33
- Ebichu
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 888
Automate celulaire
@nodgim : je suis d'accord avec ta première phrase, mais comment la démontrer ? De plus, l'état final n'est pas forcément connexe : dans ce cas, quelle est sa forme ?
Pour la question 2), ta méthode démontre que ce nombre est suffisant. Mais pourquoi est-il nécessaire ?
@masab : je ne suis pas tout à fait d'accord avec la première partie de phrase que tu mets en gras. Il faut préciser : quand je regarde les deux parties noires de droite sur ton exemple, je ne vois pas les 2 cellules dont tu parles.
La preuve que tu donnes est insuffisante pour que je comprenne : qu'appelles-tu "local", et comment passer du local au global ?
Le reste est intéressant... mais hors-sujet. Par contre tu ne réponds pas à la question 2.
@tous : l'intérêt de l'énigme ne réside pas seulement dans l'observation de ce qui se passe, ce qui n'est pas si difficile, mais dans sa démonstration. Attention, je serai pointilleux  Ça en vaut néanmoins le coup : il y a au moins un raisonnement qui est simple, élégant et difficile à trouver. Ça en vaut néanmoins le coup : il y a au moins un raisonnement qui est simple, élégant et difficile à trouver.
#7 - 25-02-2016 22:02:21
- kossi_tg
- Professionnel de Prise2Tete
- Enigmes résolues : 18
- Messages : 307
- Lieu: Montargis
automatz cellulaire
Question 1: les états finaux sont un ou plusieurs rectangles. Ces états finaux vient du simple fait qu'il ne peut exister à la fin d'angles intérieurs. On peut avoir plusieurs rectangles si initialement il existe une cellule blanche par la quelle on peut tracer une croix avec 2 droites horizontale et verticales sans toucher une cellule vivante(noire) et qu'il y a des cellules vivantes séparées d'au moins 2 cellules mortes de par et d'autre d'une de ces droites.
Question 2:
Posons B et H respectivement base et hauteur du rectangle final.
Le nombre de cellules minimum nécessaires est égal à:
(B+H)/2 si B et H sont de même parité,
(B+H+1)/2 si non.
Ces nombres sont suffisants mais sont-ils nécessaires? Oui car pour avoir un rectangle donnée, il faut disposer les cellules initiales de telle sortie qu'à chaque cellule de ce rectangle si on trace une croix comme décrite dans la réponse à la Question 1. Au final, il faut avoir dans chaque double colonne ou ligne collée au moins une cellule vivante d'où les nombres trouvés.
#8 - 25-02-2016 22:30:11
- masab
- Expert de Prise2Tete
- Enigmes résolues : 44
- Messages : 971
auyomate cellulaire
Effectivement il y a une erreur dans ma rédaction : il faut rectifier en
2 rectangles quelconques devant être distants d'au moins 2 cellules mortes
c-à-d
pour passer d'un rectangle à l'autre par une suite de cellules on doit passer sur au moins 2 cellules mortes (2 cellules consécutives doivent avoir un côté commun).
En ce qui concerne le bord :
appelons petit segment le côté d'une cellule ;
dans un état final, 2 petits segments consécutifs du bord doivent
* soit être alignés
* soit formé un angle droit, à l'intérieur duquel on a une cellule vivante
C'est ce que j'appelle propriété locale du bord.
Ceci entraîne que l'état final est un limité par un polygône convexe.
Ce ne peut être qu'un rectangle.
Il me reste effectivement la question 2.
Il suffit de la résoudre pour un rectangle axb (a cellules horizontalement, b cellules verticalement). On note n le plus petit entier >= (a+b)/2.
Alors n cellules vivantes bien choisies admettent ce rectangle pour état final.
Et on ne peut mieux faire...
#9 - 25-02-2016 23:36:51
- Ebichu
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 888
Automate cellulire
@kossi_tg : sur ma figure, à gauche, pas de "croix blanche", et pourtant c'est un état final.
À droite, il y a au moins une cellule vivante dans chaque "double colonne", et dans chaque "double ligne". Pourtant, il n'y a pas assez de cellules vivantes.
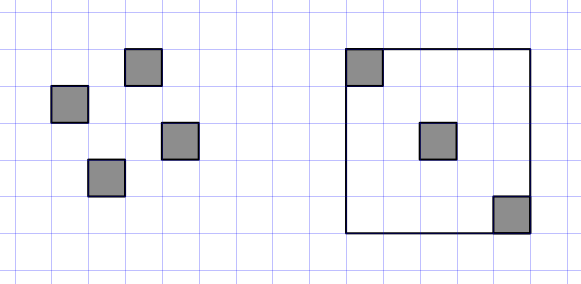
@masab : Q1 : OK pour ta rectification. En ce qui concerne le bord, comment en déduis tu qu'il s'agit d'un polygone convexe ? Deuxièmement, pourquoi ce ne peut être qu'un rectangle ? Ces deux affirmations semblent être du bon sens, mais comment les démontrer ? (en tous cas ça ne me saute pas aux yeux  ) )
Q2 : OK pour ta formule. Reste deux points à éclaircir : (1) comment bien choisir ces n cellules vivantes, et (2) pourquoi ne peut-on pas mieux faire ?
#10 - 26-02-2016 13:11:19
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
automate cellulaite
Bonjour 
Le problème est assez facile à dévisser par tâtonnement .
On appelle distance entre deux cellules la distance Manhattan entre leurs centres et distance entre deux figures la plus petite distance entre deux cases des deux figures .
Les états finaux sont les réunions de rectangles distants de plus de 2 .
Le nombre de cellules nécessaires pour envahir un rectangle mXn est E((m+n+1)/2) .
On peut facilement construire une position initiale possible en plaçant une cellule sur chaque case d'une bissectrice et de rajouter une cellule une case sur deux sur la longueur où arrive la bissectrice .
On ne peut pas faire mieux , en effet le périmètre de la figure ne varie pas durant la prolifération .
Vasimolo
#11 - 26-02-2016 14:19:13
- Ebichu
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 888
Automat cellulaire
@Vasimolo : pour la question 1, je suis d'accord avec ta réponse. Mais peux-tu la démontrer ?
Pour la question 2, c'est presque parfait  Je me permettrai juste de remettre en cause le "ne varie pas". Je me permettrai juste de remettre en cause le "ne varie pas".
#12 - 26-02-2016 14:49:52
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
AAutomate cellulaire
En effet le périmètre peut diminuer quand il y a une case à l'intérieur , heureusement ça ne change rien à la conclusion 
Pour la première partie , toute case entre deux cellules distantes de 2 doit être envahie , ce qui ne laisse aucune place à un angle rentrant .
Vasimolo
#13 - 26-02-2016 19:00:06
- Ebichu
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 888
Automate celllulaire
@Vasimolo : très bien, mais il reste une toute petite chose qui me chiffonne : comment démontrer que s'il n'y a pas d'angle rentrant, alors c'est un rectangle ?
#14 - 26-02-2016 19:05:55
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
Automate ceellulaire
Sur un quadrillage , c'est assez évident , non ?
Vasimolo
#15 - 26-02-2016 19:32:58
- Ebichu
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 888
Automate celulaire
Il est facile de s'en persuader, mais il est moins facile de le démontrer (à moins que je ne rate quelque chose d'évident). Après, je conçois que ça ne passionne pas les foules...
#16 - 26-02-2016 22:33:52
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
Automae cellulaire
Je n'ai rien contre les démonstrations un peu pointues , au contraire 
On peut dessiner un polygone qui n'est pas un rectangle sans angle rentrant et dont les côtés suivent les lignes d'un quadrillage ?
Il faudrait aussi expliquer pourquoi chaque rectangle ne peut pas être troué , pour moi c'est clair mais je ne suis pas contre un argument "canon" qui tue le problème 
Vasimolo
#17 - 27-02-2016 00:17:54
- Ebichu
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 888
automate cellulaure
J'ai bien un argument, mais pas assez canon à mon goût ; avec un peu de chance, quelqu'un proposera mieux 
#18 - 27-02-2016 11:41:00
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3839
autimate cellulaire
Je vois bien une cellule comme un cube sans couvercle et développé: les 4 cases voisines sont donc occupées par les 4 faces latérales du cube. Là où il y a recouvrement de faces, il y a naissance d'une cellule. S'il y a connexité de cellules + faces recouvertes, alors on va pouvoir agrandir ce connexe s'il n'est pas déja convexe, puisque dans un angle rentrant, il y a recouvrement.
#19 - 28-02-2016 01:29:34
- Ebichu
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 888
automaye cellulaire
@nodgim : OK pour la question 1 (si ce n'est que l'on retombe sur la discussion que j'avais avec Vasimolo juste au-dessus).
#20 - 28-02-2016 11:28:04
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
Automate cellulaaire
Bon je crois quand même qu'il y a un argument canon en faveur des rectangles distants d'au moins 3 . On considère un rectangle maximal dans chaque composante connexe de l'état final . On remarque qu'il ne peut y avoir aucune cellule voisine ou à distance 2 du bord de chaque rectangle ( sinon le rectangle n'est pas maximal ) .
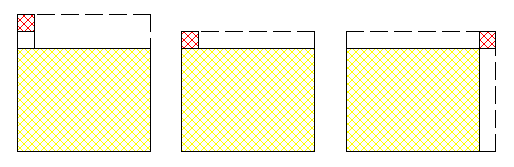
Bref les composantes connexes sont des rectangles .
Vasimolo
#21 - 28-02-2016 11:56:45
- Ebichu
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 888
Autoomate cellulaire
@Vasimolo : oui, très joli argument 
#22 - 28-02-2016 17:54:33
- portugal
- Professionnel de Prise2Tete
- Enigmes résolues : 22
- Messages : 382
automate ceklulaire
Sympa le pb. pas eu trop le temps en vacances malheureusement.
Quelques idées.
Si état final 1 pièce alors c'est un rectangle car c'est la seule figure a angle droit dont la somme absolue des angles est 360° (4 angles droits) et si la figure a plus de 360° il y a au moins un ajout possible car un angle est ouvert
Possible que le résultat final soit plusieurs rectangles séparés par 2 colonnes minimum sur les côtés et dont les sommets sont disjoints.
Pour un rectangle m,p avec p>=m
Il existe k tel que
(K-1)n +k-2 <p <= kn +k-1
Et le minimum initial est kn
Il est trivial que ca suffit car les carrés adjacents se collent
Pas la place de démontrer la réciproque dans la marge du smartphone .. . Ca faisait plaisir d'au moins participer à ce problème sympa. . . Ca faisait plaisir d'au moins participer à ce problème sympa. .
Pour la réciproque on commence par le cas carré avant de généraliser.Par recurence ca semble clair en remarquant que si le carré de taille n est atteignable ajouter une cellule permet de passer à un carré n+1
#23 - 28-02-2016 22:52:54
- Ebichu
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 888
Automate celllulaire
Merci aux participants de cette énigme, et félicitations pour vos idées diverses et originales. Je vais essayer de récapituler.
Pour la question 1, les états finaux sont des réunions de rectangles suffisamment éloignés les uns des autres. Pour formaliser cet éloignement, le message #8 de masab ou le #10 de Vasimolo (au passage, j'ai découvert la distance Manhattan) s'en chargent parfaitement. Je vous livre également ma vision avec un schéma :
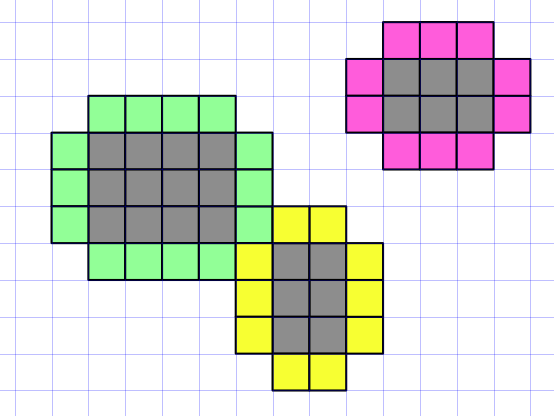
Il faut alors que les zones d'influence des rectangles (représentées en couleur) ne se recoupent pas.
Quelle que soit la définition choisie, il n'est pas difficile de voir que ces réunions de rectangles sont des états finaux. Mais, comment démontrer que tous les états finaux sont de cette forme ? Dans un état final, il ne peut y avoir d'angle rentrant. Ainsi, il reste à démontrer que si l'on considère une figure constituée de carreaux, connexe, sans angle rentrant, alors c'est un rectangle. Ça paraît évident... mais ce n'est pas si évident à démontrer. Pour cela, l'argument donné par Vasimolo dans #20 est à la fois simple, et très élégant, je doute que l'on puisse faire mieux.
Pour la question 2, vous avez été nombreux à constater que pour chaque rectangle de dimensions a*b, il fallait pour l'engendrer au minimum E((a+b+1)/2) cellules vivantes initialement. Plusieurs configurations initiales montrant que ce nombre était suffisant ont été proposées (voir par exemple les messages de dhrm77 ou nodgim).
Mais, pour démontrer qu'il était nécessaire, seul Vasimolo a trouvé l'astuce, à savoir que si l'on considère le périmètre de la partie vivante, il ne fait que décroître au cours du temps (il ne change pas quand une cellule entourée de 2 cellules vivantes naît, il décroît de 2 quand une cellule entourée de 3 cellules vivantes naît, et décroît de 4 quand une cellule entourée de 4 cellules vivantes naît). Le périmètre d'un rectangle a*b étant 2(a+b), et une cellule vivante contribuant au maximum pour 4 dans le périmètre, il faut au minimum 2(a+b)/4 cellules vivantes initialement pour engendrer ce rectangle, d'où la formule : E((a+b+1)/2) est le premier entier au moins égal à ce nombre.
|
 |

 Accueil
Accueil
 Forum
Forum