 |
#1 - 10-03-2016 12:54:36
- fix33
- Elite de Prise2Tete
- Enigmes résolues : 48
- Messages : 1198
- Lieu: Devant un clavier depuis 1748
La mouche endomie
Bonjour,
L'énigme que je vous propose aujourd'hui n'est pas nouvelle ici, mais j'ai l'espoir que certains la (re)découvriront avec plaisir.
Dans une pièce rectangulaire de 7,5 mètres de long, 3 mètres de large, 3 mètres de hauteur, vide, une araignée affamée aperçoit une mouche endormie sur le mur opposé.
L'araignée est précisément à 25 cm du sol, au centre (latéralement) du mur 3 par 3. La mouche, elle, est à 25 cm du plafond, également sur l'axe central.
La mouche risquant à tout moment de s'envoler, quelle est la distance minimale et le trajet correspondant pour atteindre son déjeuner ?
L'araignée ne peut se déplacer que sur les parois de la pièce (pas de sauts ni de fils !).
Bons petits calculs !
Fix
Je ne vien sur se site que pour faire croir que je suis treise intélligens.
#2 - 10-03-2016 13:21:44
- Ebichu
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 888
La mouche eendormie
Je dirais 10 m, en ligne droite, après avoir toutefois développé le patron de la pièce correctement (ce qui donne l'hypoténuse d'un triangle rectangle dont les côtés de l'angle droit font 6 et 8 m). Amusant 
#3 - 10-03-2016 13:39:01
- unecoudée
- Professionnel de Prise2Tete
- Enigmes résolues : 0
- Messages : 319
La mouche endoormie
bonjour.
l'araignée parcourt un 3 x3 , le sol , un côté 7.5 x 3 puis enfin le 3 x 3 où se
situe la mouche et parcourt alors:
[TeX]d = \sqrt{(1.5 + 7.5 + 0.25)^2 + (2.75 + 1.5)^2} \approx10.179636 m[/TeX]
#4 - 10-03-2016 16:10:42
- Franky1103
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 3236
- Lieu: Luxembourg
La mouche endrmie
Un parcours latéralement sur le mur donnerait une distance parcourue de:
D1 = V (2,5² + 10,5²) = V (233/2) = 10,79 m env.
Un parcours dans l'axe de la pièce par le plafond ou le sol donnerait:
D2 = 0,25 + 7,5 + 2,75 = 10,5 m, plus intéressant que D1.
Mais je sens comme un piège ...
#5 - 10-03-2016 17:02:11
- QUATTRED
- Amateur de Prise2Tete
- Enigmes résolues : 0
- Messages : 6
L amouche endormie
La distance minimum est de 10,78 m
Pour trouver cette "ligne droite", déplier les 2 faces carré de chaque coté d'un mur rectangle
on calcule l'hypoténuse d'un triangle de (1,5+7,5+1,5) sur 2,5
Il y a encore plus "direct" pourquoi me compliquer !!
En restant dans le plan passant par la mouche et l'araignée, perpendiculaire au sol et plafond, la distance est tout simplement de 0,25 + 7,5 + 2,75 soit 10,5 m
#6 - 10-03-2016 18:46:42
- gilles355
- Professionnel de Prise2Tete
- Enigmes résolues : 49
- Messages : 421
la mouvhe endormie
J'ai pas bien du comprendre l'énoncé car sinon je trouve le probleme trop simple.
Tu aurais pu rajouter une case réponse pour voir si on a juste.
10,5 mètres ??
#7 - 11-03-2016 00:44:28
- dhrm77
- L'exilé
- Enigmes résolues : 49
- Messages : 3004
- Lieu: Fanning Island-?-Lac Tele,Mali
LLa mouche endormie
Je vois que les valeurs de 7.5, 3 et 0.25 n'ont pas été prises au hasard...
Il y a 3 chemins possible:
- en allant tous droit (an passant au travers d'une seule partie longue): [latex]7.5 + 3 = 10.5[/latex]
- en partant en diagonale, en utilisant le plancher et un mur sur le coté: [latex]\sqrt{(9.25)^2+(4.25)^2} = 10.17963...[/latex]
- en partant en diagonale, et utilisant un mur sur le coté et le plafond: [latex]\sqrt{8^2+6^2} = 10[/latex] (donc en passant au travers de 3 cotés au total sur la partie longue).
Donc 10m est la distance minimale.
Great minds discuss ideas; Average minds discuss events; Small minds discuss people. -Eleanor Roosevelt
#8 - 11-03-2016 09:18:59
- enigmatus
- Expert de Prise2Tete
- Enigmes résolues : 0
- Messages : 561
aL mouche endormie
Bonjour,
C'est effectivement un problème "connu", que l'on transforme en un problème plan en dépliant convenablement la pièce.
L'araignée, qui est très intelligente, planifie son itinéraire ainsi :
- je vais rejoindre le plancher à 18,75 cm à droite de ma verticale initiale
- je me déplace ensuite sur le plancher vers le bord droit de la pièce, à 175 cm de mon mur de départ
- puis je me déplace sur le mur droit, pour rejoindre le plafond à 175 cm de l'autre extrémité de la pièce
- pour me dégourdir les jambes, je me déplace sur le plafond, pour atteindre le mur où la mouche roupille à 18,75 cm à droite de sa verticale
- je tiens le bon bout et me dirige droit sur la mouche; ce repas ne sera pas de trop pour me remettre des 10 m que j'ai dans les pattes
#9 - 11-03-2016 09:28:29
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3838
La mouche endormiee
L'araignée, en visant dans l'angle vertical du mur de la mouche, un point virtuel situé à environ 2,0607 mètres du sol, qu'elle rejoindra en ligne droite virtuelle passant par le sol et le mur latéral, parcourra 10,17963654 mètres environ.
#10 - 11-03-2016 14:27:18
- fmifmi
- Passionné de Prise2Tete
- Enigmes résolues : 18
- Messages : 87
La mmouche endormie
Sur le coup j'ai cru qu il y avait une erreur dans l’énoncé.
On déplie les murs de la pièce comme les éléments d'une boite en carton et on les pose a plat.
On trace une droite qui relie les 2 insectes
ensuite le calcul est élementaire : hypoténuse d un triangle rectangle de cotés 4.25 et 9.25
on trouve 10.180 m au lieu de :(10.50 m en se déplaçant dans un plan vertical)
l'araignée gagne 32 cm sur le trajet ce qui n'est pas évident a première vue.
par contre dans un wc çà marche pas !!! ( il faut L> 2.35m)
#11 - 11-03-2016 17:30:13
- fix33
- Elite de Prise2Tete
- Enigmes résolues : 48
- Messages : 1198
- Lieu: Devant un clavier depuis 1748
lz mouche endormie
Je suis content de voir que j'ai eu raison de poser ce problème, en apparence simple et pourtant sympa, car seuls Ebichu, Dhrm77 et Enigmatus m'ont donné la bonne valeur !
Pour info, il ne semble pas que l'un d'entre vous ait mal compris la situation géométrique. Il faut juste creuser plus 
Je ne vien sur se site que pour faire croir que je suis treise intélligens.
#12 - 11-03-2016 18:13:18
- Franky1103
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 3236
- Lieu: Luxembourg
la moiche endormie
En y réfléchissant mieux, je trouve: D = V [(3+3)² + (0,25+7,5+0,25)²] = 10 m
L'araignée passe par cinq des six faces du parallélépipède: c'est assez surprenant.
#13 - 11-03-2016 19:10:17
- unecoudée
- Professionnel de Prise2Tete
- Enigmes résolues : 0
- Messages : 319
la moyche endormie
salut.
je maintiens ma longueur de route par contre c'est juste les faces que je n'ai pas bien précisées . l'araignée parcourt dans cet ordre son mur 3x3 , un mur latéral ,
le plafond puis finalement le mur de la mouche. Mais je persiste et signe pour la
distance minimum.
#14 - 11-03-2016 20:34:53
- shadock
- Elite de Prise2Tete
- Enigmes résolues : 39
- Messages : 3334
La mouceh endormie
C'est bon je l'ai, je sais pas trop comment dessiner ça correctement sur ordinateur.
Le chemin le plus court se situe sur les bords de la pièce la ou passe un plan qui coupe la pièce en passant respectivement par le point de départ et l'arrivée.
C'est à dire que si on déplie le patron de la boite on obtient une ligne droite qui traverse 5 des 6 faces.
La réponse est donc 10m tout pile. (Pythagore dans un triangle rectangle 6 par 8)
Shadock 
"L'expérience est une lanterne qui n'éclaire que celui qui la porte." L-F. Céline
#15 - 11-03-2016 22:53:34
- kossi_tg
- Professionnel de Prise2Tete
- Enigmes résolues : 18
- Messages : 307
- Lieu: Montargis
La mouche endromie
Distance minimale: 10.5 m avec 2 trajets possibles.
1-) il descend au sol (verticalement) + va droit jusqu'au mur opposé + remonte (verticalement) = 0.25+7.5+2.75=10.5
2-) l'autre trajet le fait passer par le plafond: 2.75+7.5+0.25=10.5
#16 - 12-03-2016 00:48:19
- shadokpoilu
- Habitué de Prise2Tete
- Enigmes résolues : 45
- Messages : 26
la mouche endormue
Bonjour,
je trouve [latex]\sqrt{9,25^2+4,25^2}[/latex]
soit environ 10,18 (inférieur à 10,5 si on prend l'alignement...)
Qu'en penses-tu ? Peut-on faire mieux ? 
edit : et la réponse est oui : j'ai trouvé finalement 10 m avec [latex]\sqrt{(3+1,5*2)^2+(7,5+0,25*2)^2}[/latex]
#17 - 12-03-2016 07:48:44
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 6,181E+3
La mouche endormiee
Bonjour,
J'arrive à 10m pile.
#18 - 12-03-2016 11:39:30
- unecoudée
- Professionnel de Prise2Tete
- Enigmes résolues : 0
- Messages : 319
la mouche endoemie
salut.
finalement j'ai revu ma copie. l 'araignée parcourt son mur , le sol , un mur latéral ,
le plafond et enfin le mur opposé sur lequel est posé la mouche.
et la distance parcourue par l'araignée est :
[TeX]d = \sqrt{(0.25 + 7.5 + 0.25)^2 + (1.5 + 3 + 1.5)^2} = \sqrt{100} =10 m[/TeX]
#19 - 12-03-2016 13:17:39
- NickoGecko
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 1822
La mouche endormmie
Il aurait pu pleuvoir, con comme il est ! (Coluche)
#20 - 12-03-2016 14:31:45
- fix33
- Elite de Prise2Tete
- Enigmes résolues : 48
- Messages : 1198
- Lieu: Devant un clavier depuis 1748
la mouche endirmie
NickoGecko, Fmifmi, Quattred, Nodgim, Kossi_tg et Gilles355 : on peut faire mieux ! 
Bravo aux persévérants ! 
Oui, l'araignée a le droit de marcher au sol, au plafond et sur les murs.
Je ne vien sur se site que pour faire croir que je suis treise intélligens.
#21 - 12-03-2016 14:42:32
- cogito
- Expert de Prise2Tete
- Enigmes résolues : 48
- Messages : 593
la mouche endormue
Il y a sûrement plus simple.
#22 - 12-03-2016 15:10:35
- elpafio
- Elite de Prise2Tete
- Enigmes résolues : 43
- Messages : 1018
ka mouche endormie
Bonjour
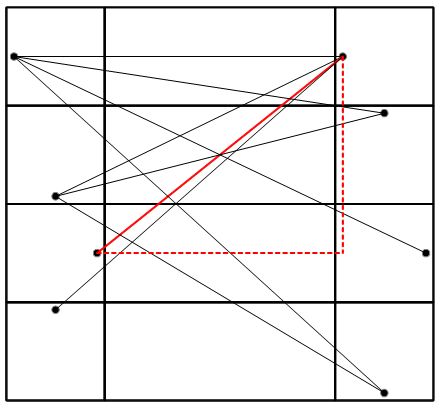
Puisque l'araignée doit rester en contact avec les surfaces, on peut faire une vue à plat. Et le chemin le plus court étant la ligne droite, ça donne quelques possibilités à étudier :

#23 - 12-03-2016 20:20:27
- kossi_tg
- Professionnel de Prise2Tete
- Enigmes résolues : 18
- Messages : 307
- Lieu: Montargis
La muoche endormie
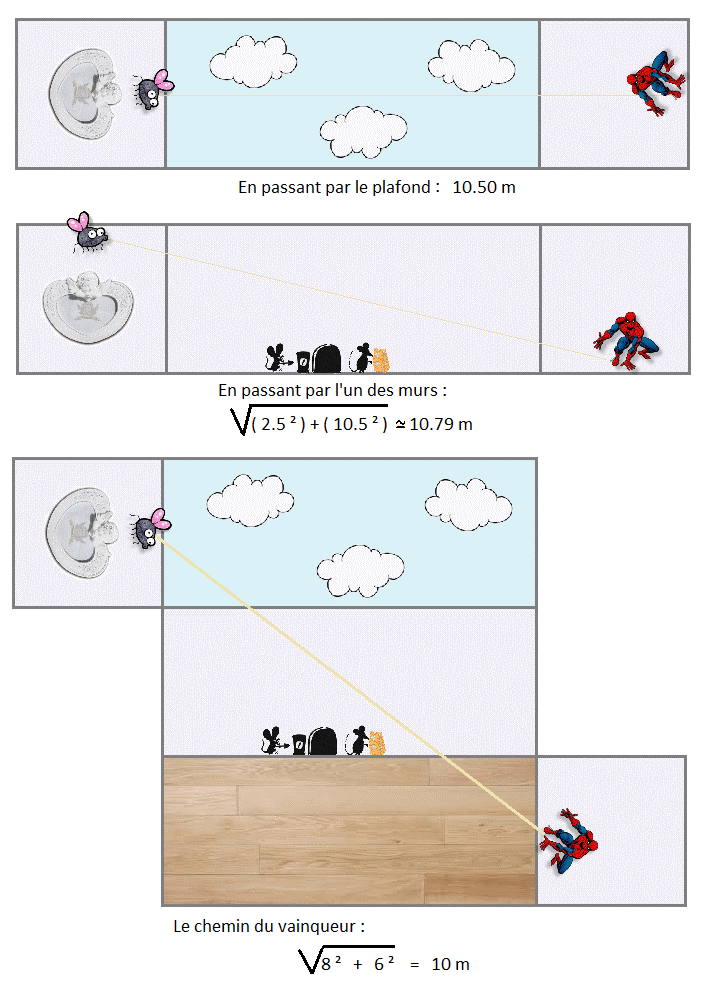
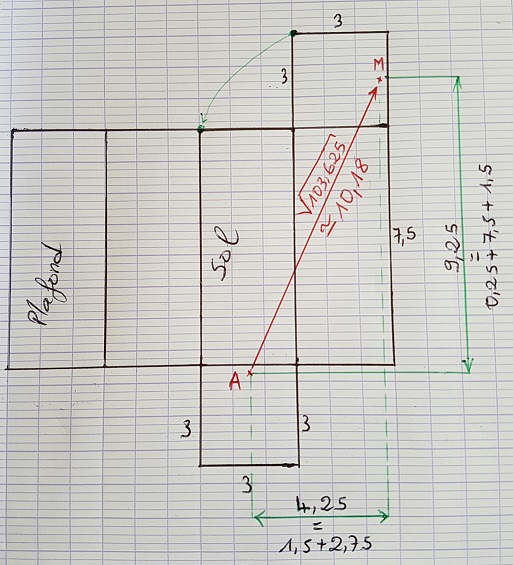
Après plusieurs erreurs de calcul  ... voilà! ... voilà!
En dépliant les parois du mur, ca apparaît plus facilement. La distance à parcourir est racine(103.625) soit environ 10.18 m.
Avec [latex]103.625=(1.5+2.75)^2+(7.5+0.25+1.5)^2[/latex]
#24 - 12-03-2016 21:03:43
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3838
la mouche rndormie
Effectivement, il y a un trajet de 10 mètres pile (V(8²+6²) en empruntant le sol le plafond et un coté.
Plutôt bluffant.
#25 - 13-03-2016 17:39:00
- kossi_tg
- Professionnel de Prise2Tete
- Enigmes résolues : 18
- Messages : 307
- Lieu: Montargis
la mouche zndormie
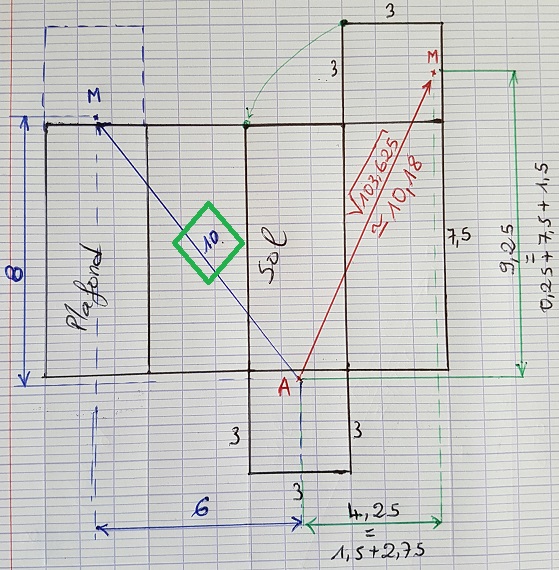
Une autre solution, mieux que la première ...
Distance à parcourir: 10 m
voir la figure:
Mots clés des moteurs de recherche
|
 |

 Accueil
Accueil
 Forum
Forum













