 |
#1 - 23-01-2017 12:53:49
- Clydevil
- Expert de Prise2Tete
- Enigmes résolues : 29
- Messages : 914
- Lieu: Seahaven island
metrpptimal
Hello!
(Ma traditionnelle image qui sert à rien mais rend le post plus vivant)
Hello!
On va construire un réseau de métro! Dans notre petite ville, il y a des stations, et deux lignes de métro. Une ligne de métro c'est simplement un cycle de stations qui peut être pris dans les 2 sens. Par exemple si on a les arrêts A,B,C,D et E dans notre ville, on peut décider de construire la ligne BDAE avec laquelle en un seul arrêt on peut aller par exemple de B à D ou E, ou de D à A ou B.
Donc comme je le disais, dans notre petite ville on ne dispose que de deux lignes, et par contrainte on aimerait pouvoir aller de n'importe quel arrêt à n'importe quel autre en deux arrêts maximum (2 segments de lignes ou moins, mais on a le droit de changer de ligne, une fois donc).
Avec ces contraintes, combien d’arrêts au maximum peut on desservir sur notre ville?
Bonne chance!
Solution:
Spoiler : [Afficher le message] @tout le monde: Merci à tous les participants, il y a au moins la solution de ebichu qui à tête validée par excel, et il semble y avoir des preuves que 16 et 17 ne sont pas possibles. Bravo donc à ceux ayant trouver une solution valide avec 15 villes!
#2 - 23-01-2017 18:32:37
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3839
metrootimal
Vu comme c'est présenté, j'imagine donc qu'une station ne peut avoir que 4 directions possibles, 2 par ligne. On suppose qu'une ligne ne déssert une station qu'une seule fois ? Si oui, alors tu ne peux pas avoir plus de 12 stations. Car 4 directions depuis n'importe quelle station, et 3 autres possibles après la 1ère station desservie. Reste à vérifier qu'on peut réaliser un tel réseau.
#3 - 23-01-2017 20:18:53
- godisdead
- Expert de Prise2Tete
- Enigmes résolues : 22
- Messages : 747
metrootimal
J'ai un réseau avec 7 stations. 2 boucles de 5 arrêts avec 3 stations en commun.
#4 - 23-01-2017 20:42:34
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 6,194E+3
metroptimak
Je dirais intuitivement 11 stations, dont la solution est relativement simple.
Au-delà, j'ai de sérieux doutes.
#5 - 23-01-2017 21:26:30
- Clydevil
- Expert de Prise2Tete
- Enigmes résolues : 29
- Messages : 914
- Lieu: Seahaven island
Mettroptimal
@nodgim: Avoir une majoration et ensuite trouver un réseau qui l’atteint est une bonne démarche. Mais je ne suis pas d'accord avec ta majoration 
@godisdead: On peut faire mieux.
@gwen27: Il y a une majoration qui est plus grande que ta proposition et qui semble avoir beaucoup de marge, je n'ai pas la solution moi même mais je serais étonné que la marge ne soit pas suffisante pour faire mieux. A creuser.
#6 - 23-01-2017 22:48:21
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 6,194E+3
letroptimal
Si on ne peut pas repasser 2 fois par le même point pour un trajet : 11
Sinon, autant que l'on veut.
#7 - 24-01-2017 07:46:55
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3839
metropyimal
Oui, j'ai tout simplement mal compté, le max est 17 et non 12.
Reste à construire les liaisons qui vont avec. Ce n'est pas le plus facile....
#8 - 24-01-2017 10:18:13
- Ebichu
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 888
Mertoptimal
J'ai une majoration avec 17 sommets, pardon, "arrêts" :
* Chaque sommet est de degré 2 ou 4 suivant qu'il est situé sur une ou deux lignes, donc au plus 4.
* Prenons un sommet S. S est relié à au plus 4 sommets, et chacun de ces 4 sommets, à au plus 3 autres. Quant aux autres sommets, ils seraient à une distance de S supérieure à 2. 1+4+4*3=17, cqfd.
Sinon, voici une solution avec 13 sommets :
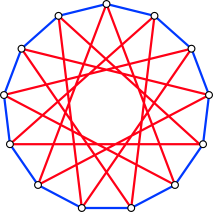
Je n'ai pas encore beaucoup cherché et je ne vois pas a priori de raison pour laquelle ce ne serait pas possible avec 17. Je continue à réfléchir.
#9 - 24-01-2017 10:24:10
- Clydevil
- Expert de Prise2Tete
- Enigmes résolues : 29
- Messages : 914
- Lieu: Seahaven island
Metrptimal
@Ebichu: Très bien! on en est au même point. Il y a sans doute encore mieux. A creuser.
@Gwen27: On a pas forcement le max pour le moment mais au moins on a strictement mieux que ta proposition.
#10 - 24-01-2017 11:51:58
- Ebichu
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 888
meyroptimal
Et voici une solution avec 15 sommets :
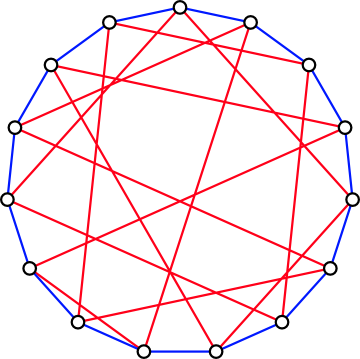
Ça devient de plus en plus tendu, donc j'ai bon espoir, soit de trouver un graphe pour 16 ou 17, soit de montrer que ça ne peut exister.
Note pour plus tard : faire une version plus lisible de ce sac de noeuds 
#11 - 24-01-2017 11:59:08
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3839
letroptimal
Il y a des solutions simples pour 11 et 13 stations.
Pour 11, la ligne 1 prend les stations de 1 à 11 dans l'ordre (puis retour à 1), la ligne 2 dessert, après la station n, la station n+4 modulo 11.
Pour 13, la ligne 1 prend les stations de 1 à 13 dans l'ordre (puis retour à 1), la ligne 2 dessert, après la station n, la station n+5 modulo 13.
ça se passe bien avec 11 et 13 qui sont premiers, ça permet d'avoir un pas unique pour la ligne 2. Avec ces constructions, si ça marche pour une station, ça marche forcément pour les autres.
#12 - 25-01-2017 08:04:31
- Franky1103
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 3238
- Lieu: Luxembourg
metroprimal
Ma ligne de métro, en forme de fleur à pétales, est constituée de n+1 stations: une station centrale O et n stations périphériques S(n). Le cheminement en boucle du métro est: O – S(1) – O – S(2) – O S(3) – O – …..– O – S(n) – O – S(1). Pour les besoins de l’énigme, je peux superposer une seconde ligne identique centrée aussi sur O. De cette manière, je peux passer de n’importe quelle station en maximum deux arrêts.
Avec ce réseau, je pourrai avoir une infinité de stations répondant à la question, mais sans doute non conforme à l’esprit de ton énigme. Faut-il rajouter dans l’énoncé qu’un cycle de stations ne doit jamais repasser deux fois par la même station ?
#13 - 25-01-2017 08:44:32
- Clydevil
- Expert de Prise2Tete
- Enigmes résolues : 29
- Messages : 914
- Lieu: Seahaven island
Mteroptimal
@Franky1103: Oui, c'est trivial que sans contrainte de ne pas repasser par la même station une seule ligne (même pas besoin de 2) peut faire tous les segments, et donc à elle seule garantir de desservir tout à tout en un seul arrêt (même pas besoin de 2). Donc en effet oui, une ligne est un cycle qui ne contient chaque station au maximum qu'une seule fois 
#14 - 25-01-2017 15:55:46
- Ebichu
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 888
Mteroptimal
C'est impossible pour 16 ou 17 sommets.
Remarquons déjà que s'il existe un sommet de degré 2, les deux sommets auxquels il est relié ne peuvent eux-même être reliés qu'à 3 autres sommets chacun, aussi il y a au plus 1+2+3*2=9 sommets dans le graphe.
Tous les sommets sont donc de degré 4 (chaque station est parcourue par les deux lignes de métro).
Ensuite, je suis allé faire un tour sur cette page : https://fr.wikipedia.org/wiki/Lexique_d … es_graphes
On cherche un graphe 4-régulier (tous les sommets sont de degré 4), et de diamètre 2 (la distance maximale entre deux sommets est 2) ; le graphe doit aussi être décomposable en deux cycles disjoints, élémentaires et même hamiltoniens (les deux lignes de métro), mais ceci n'est pas nécessaire pour conclure.
Sur ce lien : http://ijact.org/volume4issue5/IJ0450003.pdf il y a une démonstration du fait qu'il n'existe pas de graphe 4-régulier de diamètre 2 à 17 ou 16 sommets. C'est un peu lourdingue comme démonstration (il y a plein de petites étapes), l'anglais n'est pas très bon et le formalisme exagéré, mais ça marche.
Enfin, si j'en crois le titre de cet article, il a été démontré qu'il n'y a qu'une solution pour 15 sommets :
H. J. Broersma, A. A. Jagers, The unique 4-regular graphs on 14 and 15 vertices
with diameter 2, Ars Combinatoria 25 (C) (1988) 55–62.
Je suppose que ça peut se démontrer avec des arguments du même type que pour 16 et 17. Il y a peut être plus élégant.
#15 - 25-01-2017 18:59:14
- Clydevil
- Expert de Prise2Tete
- Enigmes résolues : 29
- Messages : 914
- Lieu: Seahaven island
metroptomal
@Ebichu:

#16 - 27-01-2017 18:06:50
- Franky1103
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 3238
- Lieu: Luxembourg
Mteroptimal
Avec deux lignes, je ne fais pas mieux que six stations,  sachant qu'avec une seule, on est déjà à cinq. sachant qu'avec une seule, on est déjà à cinq.
#17 - 28-01-2017 11:15:19
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 6,194E+3
Metroptima
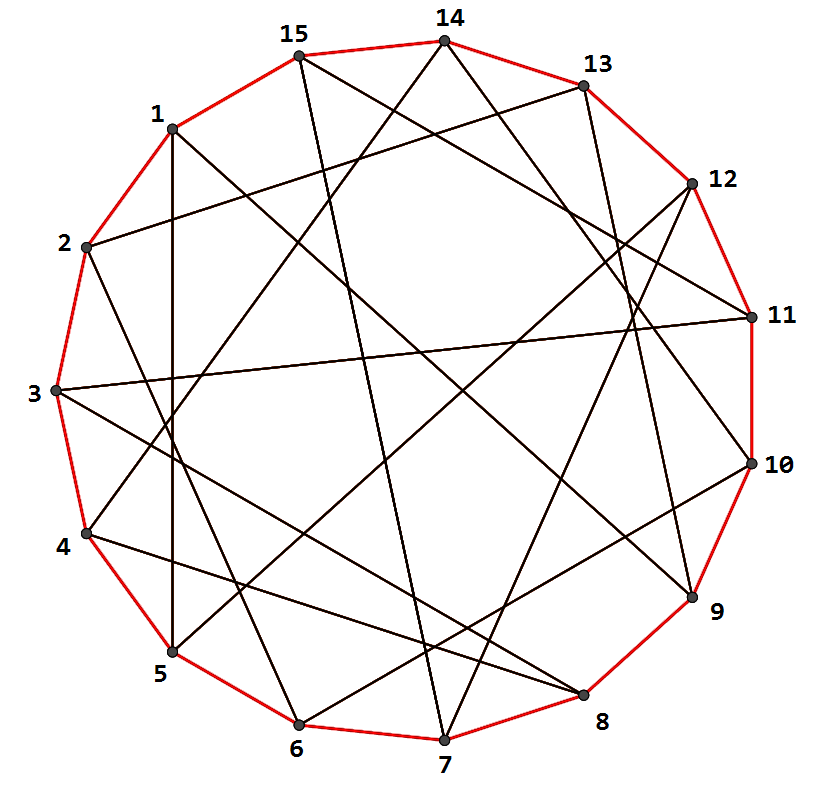
Effectivement, mauvais raisonnement pour 11 car les trajets ne sont pas orientés, une ligne c'est deux voies...
Et donc, la limite extrème théorique devient 17 : ça parait difficile à atteindre.
16 est peut-être vraisemblablement possible, mais je ne trouve que pour 15 pour l'instant...
#18 - 29-01-2017 17:22:38
- golgot59
- Elite de Prise2Tete
- Enigmes résolues : 48
- Messages : 1494
- Lieu: Coutiches
metrpptimal
Salut !
Très intéressant comme problème. J'ai trouvé 9 villes... (j'ai laissé mes 1ers essais avant d'arriver à ce résultat)
Je ne sais pas si on peut faire mieux...
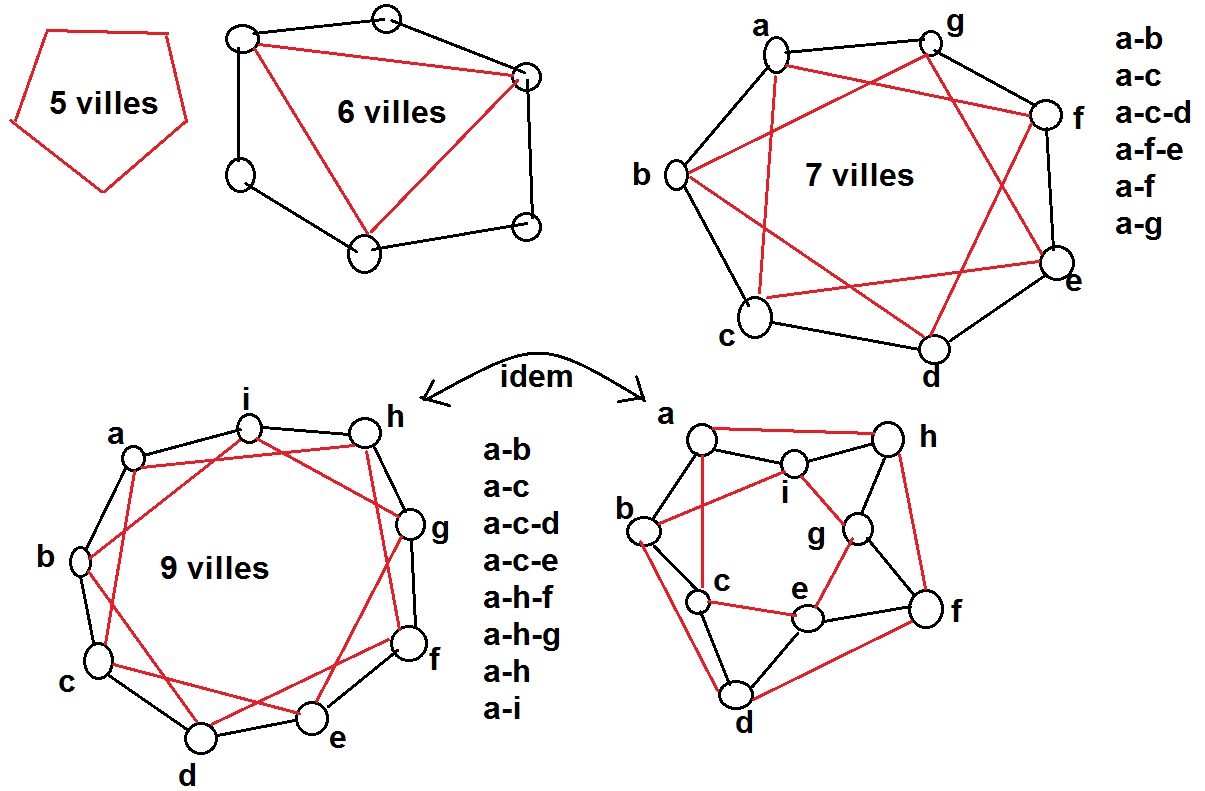
Sur le 1er à 9 villes, on voit bien le principe, sur le second, on visualise mieux le circuit du 2ème métro.
#19 - 29-01-2017 17:40:52
- golgot59
- Elite de Prise2Tete
- Enigmes résolues : 48
- Messages : 1494
- Lieu: Coutiches
Metroptiml
En fait voilà mieux avec le même principe : 11 villes
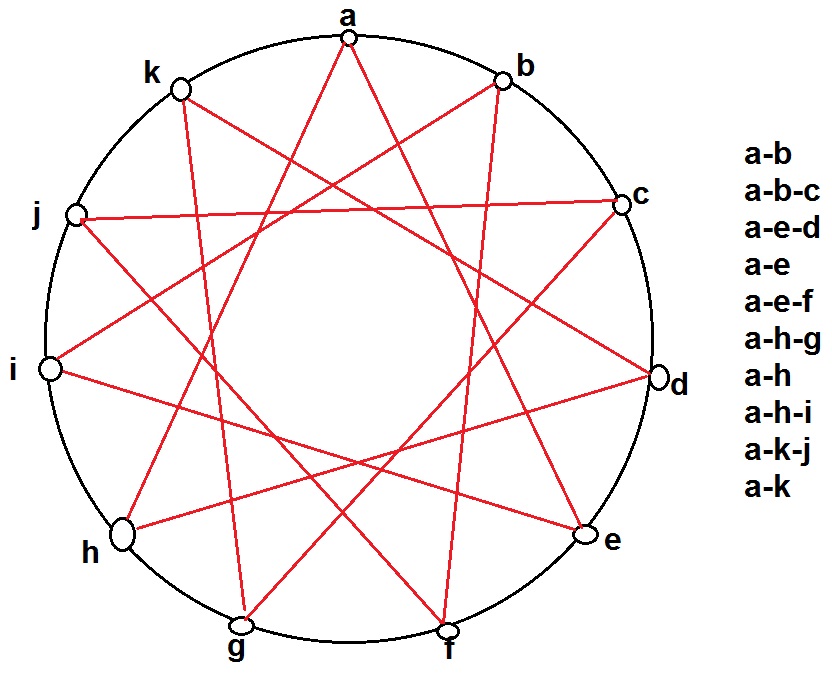
Avec cette méthode c'est le max car chaque ville n'est atteignable que par un seul circuit.
Mais peut-être existe-t-il mieux autrement...
#20 - 30-01-2017 11:25:46
- Franky1103
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 3238
- Lieu: Luxembourg
Metroptimmal
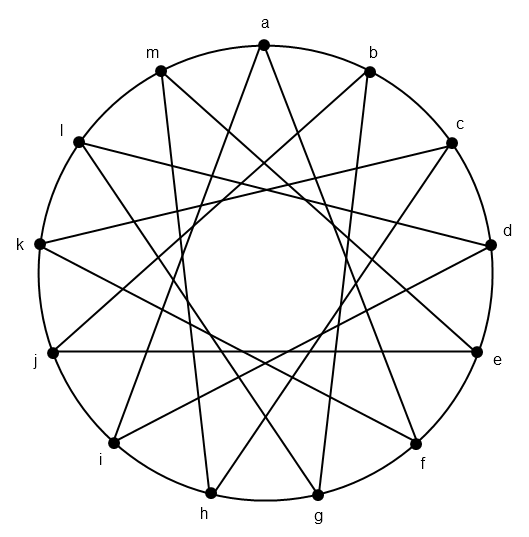
Avec le réseau à 11 villes de golgot59, on ne profite pas de la possibilité de deux trajets longs. Voici ce que cela donne avec un réseau à 13 villes:
a-b / a-b-c / a-i-d / a-f-e / a-f / a-f-g / a-i-h / a-i / a-i-j / a-f-k / a-m-l / a-m
Mais est ce l’optimum ?
Avec le réseau à 15 villes de gwen27, sauf erreur de ma part, on ne n’arrive pas à passer de 1 à 7 ou de 1 à 11 au moins de 3 arrêts.
Par symétrie par rapport aux stations qui peuvent toutes être le point de départ, le réseau devra certainement être en forme de rosace régulière.
#21 - 30-01-2017 11:51:09
- Clydevil
- Expert de Prise2Tete
- Enigmes résolues : 29
- Messages : 914
- Lieu: Seahaven island
Metrooptimal
@Franky1103: pour le réseau de gwen 1-15-7 1-15-11.
@tout le monde: Merci à tous les participants, il y a au moins la solution de ebichu qui à tête validée par excel, et il semble y avoir des preuves que 16 et 17 ne sont pas possibles. Bravo donc à ceux ayant trouver une solution valide avec 15 villes!
#22 - 30-01-2017 12:58:03
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 6,194E+3
Metroptimall
Mon réseau fonctionne.
Sous forme de matrice :
0 1 0 0 1 0 0 0 0 0 0 1 0 0 1
1 0 1 0 0 1 0 0 1 0 0 0 0 0 0
0 1 0 1 0 0 0 0 0 0 1 0 1 0 0
0 0 1 0 1 0 0 1 0 0 0 0 0 0 1
1 0 0 1 0 1 0 0 0 1 0 0 0 0 0
0 1 0 0 1 0 1 0 0 0 0 0 1 0 0
0 0 0 0 0 1 0 1 0 0 1 0 0 0 1
0 0 0 1 0 0 1 0 1 0 0 1 0 0 0
0 1 0 0 0 0 0 1 0 1 0 0 0 1 0
0 0 0 0 1 0 0 0 1 0 1 0 0 1 0
0 0 1 0 0 0 1 0 0 1 0 1 0 0 0
1 0 0 0 0 0 0 1 0 0 1 0 1 0 0
0 0 1 0 0 1 0 0 0 0 0 1 0 1 0
0 0 0 0 0 0 0 0 1 1 0 0 1 0 1
1 0 0 1 0 0 1 0 0 0 0 0 0 1 0
La matrice au carré :
4 0 1 2 0 2 1 1 1 1 1 0 1 1 0
0 4 0 1 2 0 1 1 0 1 1 1 2 1 1
1 0 4 0 1 2 1 1 1 1 0 2 0 1 1
2 1 0 4 0 1 2 0 1 1 1 1 1 1 0
0 2 1 0 4 0 1 1 1 0 1 1 1 1 2
2 0 2 1 0 4 0 1 1 1 1 1 0 1 1
1 1 1 2 1 0 4 0 1 1 0 2 1 1 0
1 1 1 0 1 1 0 4 0 1 2 0 1 1 2
1 0 1 1 1 1 1 0 4 1 1 1 1 1 1
1 1 1 1 0 1 1 1 1 4 0 1 1 1 1
1 1 0 1 1 1 0 2 1 0 4 0 2 1 1
0 1 2 1 1 1 2 0 1 1 0 4 0 1 1
1 2 0 1 1 0 1 1 1 1 2 0 4 0 1
1 1 1 1 1 1 1 1 1 1 1 1 0 4 0
0 1 1 0 2 1 0 2 1 1 1 1 1 0 4
Leur somme :

On retrouve l'ordre 4 en diagonale, logique... et 2 trajets en double pour chaque nombre.
Malheureusement, pour des raisons de symétrie, ça ne laisse que 15 liaisons de libres. Il en faudrait 16 pour rajouter un 16e point.
Il est rigolo de voir que je me suis amusé avec un parcours de cavalier pour construire la matrice noire. Je suis presque certain que celle d'ebichu présenterait la même particularité.
#23 - 30-01-2017 15:06:47
- Franky1103
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 3238
- Lieu: Luxembourg
Meroptimal
@gwen27: Effectivement ton réseau fonctionne: mille excuses. Je ne devais pas être réveillé ce matin ou déjà endormi (je travaille de nuit). Le plus surprenant est que ce n'est pas une rosace régulière.
#24 - 30-01-2017 22:57:03
- Ebichu
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 888
Metropttimal
@gwen27 : je ne comprends pas de quel parcours de cavalier tu parles, mais je suis également certain que mon graphe présente la même propriété, car c'est le même que le tien - et pour cause, il n'en existe qu'un seul. C'est d'ailleurs un exercice pas si simple que de démontrer que nos deux graphes sont isomorphes. Je ne connais pas de programme qui fasse ça, alors je l'ai fait à la main avec Geogebra, et ça marche.
|
 |

 Accueil
Accueil
 Forum
Forum














