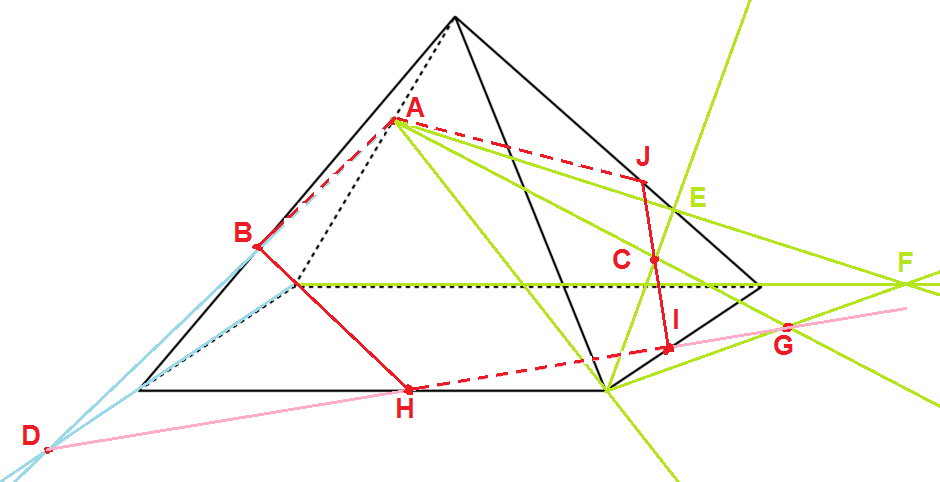
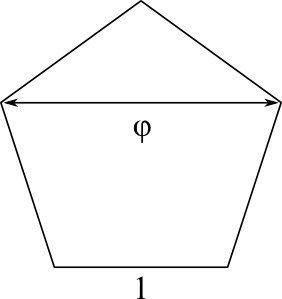
Enigme The golden pyramid (part 2) + INDICE @ Prise2Tete

Ebichu · #1

Bonjour à tous,

je reprends la pyramide de l'énigme précédente, une pyramide dont la base est un carré de côté 1, avec le sommet à la verticale du centre de la base.

Si je vous dis que sur le tracé de golgot59, la section ABHIJ est un pentagone régulier, pouvez-vous en déduire la hauteur de la pyramide ?

Pour paraphraser nodgim, ne vous égarez pas : il est facile de se perdre dans des calculs horribles avec des polynômes de degré 8... mais il est possible aussi de s'en tirer avec des calculs accessibles au niveau 1e, si on s'y prend bien. A priori, c'est un problème difficile.

Bon courage

Indice :

Spoiler : [Afficher le message]

leresolus · #2

Bonjour,

Je ne comprends pas la question.

Si la perspective cavalière est exacte la hauteur de la pyramide est proportionnel a la base de valeur 1 puisque dans une perspective cavalière les hauteurs sont en vrai grandeur comme les lignes horizontales .

Cordialement

Ebichu · #3

@leresolus : certes, mais une figure ne donne qu'une approximation. Mesurer sur ma figure ne procurera pas une valeur exacte de la hauteur.

Formulé autrement : on a une pyramide, dont la base est un carré de côté 1, et dont le sommet est à la verticale du centre du carré. La section de cette pyramide par un plan donne un pentagone régulier. Quelles sont les valeurs possibles pour la hauteur de cette pyramide ?

leresolus · #4

Bonjour,

Sur le lien suivant ma réponse.

Cordialement

http://www.prise2tete.fr/upload/leresolus-PYRAMIDE2.pdf

Ebichu · #5

@leresolus : c'est parfait pour c et d, félicitations ! La démarche pour obtenir ces valeurs m'intéresse

En revanche, h et la mesure de l'angle dans un plan vertical, quoique très proches de la bonne réponse, ne sont qu'approximatifs.

leresolus · #6

Pour c je n'ai pas de mérite j'ai trouvé la valeur sur internet.
Apres j'ai construit a partir de cette valeur et calculer l'angle et la valeur
de l'angle et la hauteur de la pyramide simplement par résolution des triangles.

Ebichu · #7

En effet cette démarche est imparable

Ebichu · #8

Merci à leresolus pour sa participation, et à ceux qui ont cherché.

Je me suis posé ce problème sans savoir s'il y avait une solution, et j'ai pas mal galéré avant d'y arriver. Le jeu en valait la chandelle car le résultat est joli : une seule pyramide convient, c'est le demi-octaèdre régulier (hauteur = racine(2)/2).

Ma démonstration utilise les coordonnées, je peux la détailler si ça intéresse quelqu'un. Quand on l'a sous les yeux ce n'est pas difficile à comprendre.

A posteriori j'ai googlé, et j'ai vu que, sans surprise, le problème était connu :

https://fr.wikipedia.org/wiki/Coupe_pen … arr%C3%A9e

Forum dédié aux énigmes et à toutes formes de jeux de logique.	Déconnexion
Tu n'es pas identifié sur Prise2tete : s'identifier. Accueil Forum	[+]

#1 - 30-11-2017 10:46:24

The golden pyramid (part 2 + INDICE

#0 Pub

#2 - 01-12-2017 16:00:24

The golden pyramid (pat 2) + INDICE

#3 - 01-12-2017 18:05:09

the golden pyramid (pary 2) + indice

#4 - 02-12-2017 14:23:05

the golden pytamid (part 2) + indice

#5 - 02-12-2017 16:58:50

The gloden pyramid (part 2) + INDICE

#6 - 02-12-2017 17:36:44

The golden pyramid (part 2) + IINDICE

#7 - 02-12-2017 18:16:38

The glden pyramid (part 2) + INDICE

#8 - 06-12-2017 22:10:53

the folden pyramid (part 2) + indice

Réponse rapide

Sujets similaires

Pied de page des forums