|
#1 - 22-04-2018 08:13:15
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
#2 - 22-04-2018 09:38:46
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3839
Mage 6
Je ne sais pas si c'est ce que tu as attend, mais si on part de la couleur qu'on veut ajouter en haut de la pyramide, c'est très facile par déduction de retrouver la couleur en bas, puisque l'algorithme est réversible.
Cela dit, l'astuce est peut être de chercher la solution sur la base de la pyramide plutôt que sur la pente.
#3 - 22-04-2018 10:03:27
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
mzgie 6
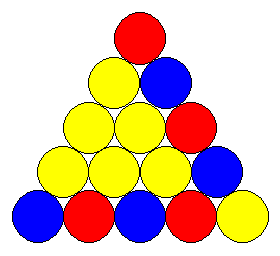
Non , l'algorithme n'est pas réversible , sous un B on peut avoir BB , JR ou RJ ce qui multiplie les possibilités au fil des étages .
Et pourquoi ?
Vasimolo
#4 - 22-04-2018 10:49:26
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3839
agie 6
Je me suis mal fait comprendre.
Mettons que l'on veuille faire un ajout de jetons sur le flanc gauche d'une pyramide de hauteur 5 et que les jetons du flanc gauche, de bas en haut, soient 11223. Si on veut 1 en haut, il faut 2 en bas. 3+1 = 2; 2+2=2; etc...
C'est dans ce sens là que je parlais de réversibilité. Si a + b = c alors a + c = b.
#5 - 22-04-2018 11:14:57
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
mafie 6
D'accord , mais comment prévoir le flanc gauche et surtout comment être sûr d'obtenir la bonne couleur au sommet et comment ?
Vasimolo
#6 - 22-04-2018 15:42:43
- enigmatus
- Expert de Prise2Tete
- Enigmes résolues : 0
- Messages : 561
mzgie 6
Bonjour Vasimolo,
On représente les couleurs par les valeurs 0, 1, 2.
Avec une base de N jetons, numérotés de 0 à N-1, la valeur du jeton au sommet est donnée par l'expression :
{ (-1)**(N-1) * [somme, pour j=0->N-1 ( jeton(j) * cnp(N-1,j) ) ] } modulo 3
On peut remplacer les coefficients du binôme dans l'expression par leur valeur modulo 3.
Pour N=10, il se trouve que seuls les 2 jetons des extrémités interviennent, et on retrouve la règle initiale des triangles de base, à savoir : j3 = ( -j1 - j2 ) modulo 3.
Édité : Ajout de la dernière formule
#7 - 22-04-2018 18:24:23
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3839
Magiie 6
" D'accord , mais comment prévoir le flanc gauche et surtout comment être sûr d'obtenir la bonne couleur au sommet et comment ? "
On dit bien dans l'énoncé qu'on regarde la "réalisation", c''est à dire la pyramide, pour ce que je comprends. La question que je pose autrement : la seule analyse de la chaîne de départ suffit elle à prévoir la couleur du jeton au sommet ?
#8 - 22-04-2018 18:50:43
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
magiz 6
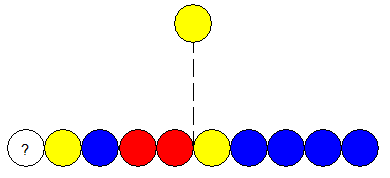
Non Nodgim , le magicien regarde simplement la ligne initiale de 9 pions .
Vasimolo
#9 - 22-04-2018 18:55:37
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
mafie 6
@Enigmatus : je suis d'accord avec la réduction de ta formule mais tu l'expliques comment ?
Vasimolo
#10 - 22-04-2018 20:11:31
- enigmatus
- Expert de Prise2Tete
- Enigmes résolues : 0
- Messages : 561
Maige 6
Vasimolo #9 a écrit:@Enigmatus : je suis d'accord avec la réduction de ta formule mais tu l'expliques comment ?
C'est parce que, pour j=1->8, les coefficients du binôme cnp(9,j) sont des multiples de 3, et n'interviennent pas dans le résultat.
#11 - 23-04-2018 07:38:42
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3839
Magei 6
Soit n-k, le k-ième jeton de la n-ième ligne (en partant du bas) de la pyramide.
On a la relation générale : n-k + (n-1)-k + (n-1)-(k+1) = 0 [3]
On peut en déduire une valeur [3] pour n-k :
n-k = - (n-1)-k - (n-1)-(k+1)
= (n-2)-k + 2 (n-2)-(k+1) + (n-2)-(k+2)
= - (n-3)-k - 3 (n-3)-(k+1) - 3 (n-3)-(k+2) - (n-3)-(k+4)
=......
On reconnait les coefficients du triangle de Pascal. Bien entendu, on peut se contenter de ne donner que leurs valeurs modulo 3.
Il se trouve que pour n = 10 on obtient que des 0 pour les coefficients intermédaires, et donc :
10-1 = -(1-1) - (1-10)
Il suffit de regarder les 2 jetons d'extrémité à la base de la pyramide et d'appliquer la règle comme si le jeton tout en haut était juste au dessus des 2 jetons considérés comme joints.
#12 - 23-04-2018 12:51:06
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
Magi e6
C'est bon Enigmatus et Nodgim 
Vasimolo
#13 - 23-04-2018 17:33:36
- Ebichu
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 888
Maagie 6
Les trois jetons aux extrémités de la pyramide de taille 10 vérifient la même règle que trois jetons formant une pyramide de taille 2.
Je ne détaille pas faute de temps et car je pense que certains ont fait ça mieux que moi, mais c'est lié au fait que dans la 10e ligne du triangle de Pascal, seuls les deux "1" aux extrémités ne sont pas divisibles par 3. Je peux préciser ma pensée si nécessaire.
#14 - 23-04-2018 17:42:27
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
Magie
Beaucoup sont passés par le triangle de Pascal , j'ai fait un peu différemment 
Le masque sera levé dans quelques heures et je ne suis pas sûr qu'il soit utile d'ajouter du temps .
Vasimolo
#15 - 24-04-2018 11:43:02
- scarta
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 1986
aMgie 6
Dommage, j’arrive après la bataille ou presque. On note les couleurs 0,1 et 2
Un pion est calculé en faisant la somme de ses deux parents, et en prenant l’opposé, modulo 3
On associe au pion sommet le nombre 1
En redescendant la pyramide, on additionne les valeurs du ou des enfants (on gros c’est le triangle de Pascal), ce qui nous donne le nombre de fois où un pion de départ est utilisé
Il faut donc considérer la 9eme ligne du triangle de Pascal, et en plus modulo 3. Magique : tout est nul sauf les bords.
Il suffit donc d’appliquer la même règle que pour la construction aux deux pions « sommets » pour trouver le 3ème.
J’aurai aimé pouvoir formaliser un peu plus
#16 - 24-04-2018 19:07:27
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
Magie
Je peux ajouter un peu de temps si tu veux formaliser un peu plus mais l'idée est là 
Vasimolo
#17 - 25-04-2018 08:01:23
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
Maagie 6
Nous avons tous eu à peu près la même idée avec du modulo 3 .
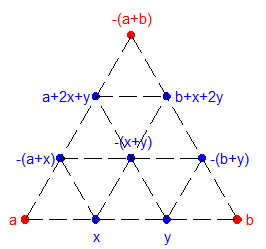
On remarque que pour chaque petit triangle équilatéral de couleurs a , b et c on a a+b+c=0 [modulo 3] . On retrouve cette même égalité aux sommets de chaque triangle équilatéral de côté 3 ( 4 points sur chaque arête ) et par voie de conséquence du grand triangle de côté 9 . Si on note « a » la couleur non sélectionnée à la base et « b » la couleur souhaitée en haut , on choisira la couleur c telle que a+b+c=0 à l’extrémité désignée .
Merci aux participants 
Vasimolo
#18 - 25-04-2018 10:49:39
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3839
Magie
Oui, et donc aussi pour toute chaîne de longueur 3^n + 1.
Mots clés des moteurs de recherche
|
 |

 Accueil
Accueil
 Forum
Forum