 |
#1 - 29-04-2020 17:08:48
- caduk
- Professionnel de Prise2Tete
- Enigmes résolues : 45
- Messages : 398
Déformation d'nu treillis
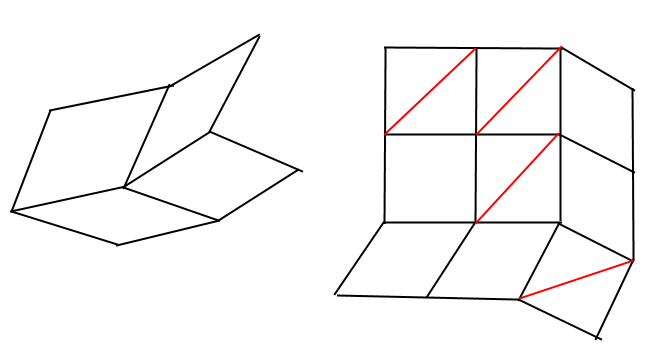
Bonjour à tous,
On dispose d'un treillis métallique composée de barres toutes de même longueur et agencée de manière à former des cellules carrées. Cependant, les barres peuvent pivoter autour de leurs liaisons et tourner librement les unes par rapport aux autres, mais seulement dans l'axe du treillis (le treillis reste donc contenu dans le plan, les images ne sont donc pas en 3d mais dans le plan, hein  ). Les cellules peuvent donc se déformer (comme à gauche). On peut cependant choisir de rigidifier certaines cellules pour les forcer à rester carrées (comme à droite). ). Les cellules peuvent donc se déformer (comme à gauche). On peut cependant choisir de rigidifier certaines cellules pour les forcer à rester carrées (comme à droite).
En rigidifiant certaines cellules, d'autres cellules non rigidifiées deviennent aussi rigide. Par exemple à droite, la cellule touchant trois cellules rigidifiées devient également rigide, car pour la déformer, il faudrait déformer l'une de ces 3 cellules...
A quelles conditions l'intégralité d'un treillis sera rigide? Quel est le nombre minimal de cellules à rigidifier pour avoir un treillis intégralement rigide? Peut-on vérifier efficacement si un treillis est intégralement rigide?
#2 - 30-04-2020 17:55:26
- unecoudée
- Professionnel de Prise2Tete
- Enigmes résolues : 0
- Messages : 319
Déformation 'un treillis
bonjour;
Avec un treillis de n x m mailles carrées ; on part du carré du coin supérieur gauche par exemple qu'on va trianguler ; on continue avec un carré voisin ( carré ayant un côté commun )
On continue comme ça jusqu'à trianguler le carré en bas à droite .
On aura ainsi triangulé tout l'ensemble sur le plan avec n+m-1 diagonales .
Chaque maille , en dehors des 2 mailles extrêmes , possède 2 mailles voisines triangulées . Sur l'exemple , il suffit de trianguler le sixième ou le huitième carré .
On triangule alors un 3 x 3 avec 3 + 2 = 5 barres .
#3 - 30-04-2020 22:21:23
- Jackv
- Elite de Prise2Tete
- Enigmes résolues : 34
- Messages : 3615
- Lieu: 94110
éDformation d'un treillis
A première vue, je suppose que si ton treillis comporte N rangées et M colonnes et que ces rangées ou colonnes sont continues (mais quelles soient complètes ou non), il faut qu'il y ait au moins N + M - 1 cellules rigides pour que l'ensemble soit rigide.
#4 - 01-05-2020 00:04:56
- caduk
- Professionnel de Prise2Tete
- Enigmes résolues : 45
- Messages : 398
Déformation d'un triellis
Bonjour à vous deux, c'est effectivement le nombre minimal pour rigidifier, reste à trouver une démo 
#5 - 01-05-2020 17:32:48
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 6,193E+3
Déformaation d'un treillis
Il en faut m+n-1.
C'est suffisant, on le voit en rigidifiant deux côtés.
De proche en proche, le quatrième morceau d'un carré dont 3 parties sont rigides l'est aussi.
C'est nécessaire.
On peut réduire le treillis d'une ligne ou colonne, si on suppose tout le reste rigide et que cette ligne ou cette colonne contient au moins un morceau rigide.
En m+n-2 étapes , on retire au minimum m+n-2 morceaux rigides, et le dernier doit l'être aussi, pour que la récurrence soit valable.
Mais ce n'est pas pour autant que la maille sera rigide, il faut que les morceaux soient disposés de manière à permettre cette réduction. Il n'est même pas nécessaire d'avoir des "groupes de 3". Et la solution est toujours possible car avec m<=n il y aura toujours une ligne ou une colonne avec 1 case fixée ou moins.
#6 - 02-05-2020 11:30:06
- TOUFAU
- Professionnel de Prise2Tete
- Enigmes résolues : 0
- Messages : 105
Déformatino d'un treillis
Bonjour Caduk.
Un test simple de rigidité (ou non) du treillis dans son ensemble : vérifier qu’aucun cisaillement entre les cellules de deux de ses coins opposés n’est possible.
Le nombre minimum de cellules à rigidifier pour qu’un treillis (n,p) soit rigide : n+p-1.
On peut montrer qu’un treillis est rigide <=> deux cellules de coins opposés sont figées l’une vs l’autre (figées= aucun déplacement ou aucune rotation possible).
Si deux cellules opposées sont non figées entre elles, le treillis n’est pas rigide, évidemment…
Si deux cellules opposées sont figées entre elles, on peut montrer par récurrence que le treillis est rigide.
D’abord, la question est de savoir sous quelle condition deux coins opposées sont figés entre eux.
Dans les faits, cela signifie qu’un ‘chemin rigide’ existe entre ces deux coins, via des cellules figées entre elles par leurs arrêtes (sinon la rotation reste possible), ce qui propage la contrainte entre les coins. Que les cellules du chemin en question soient rigides de façon forcée ou pas.
Pour un treillis (n,1), les cellules opposées sont figées entre elles si toutes les cellules sont rigides, de façon assez immédiate. Le treillis est donc rigide.
Pour un treillis (2,2), il faut 3 cellules rigidifiées pour figer les coins opposés entre eux. Dès lors qu’ils sont figés, la dernière cellule l’est aussi, le treillis est rigide.
Imaginons que ce soit vrai pour des treillis (n,p) et (n-1,p+1). ie coins opposés figés => treillis rigides.
Ajoutons une colonne. Si un des nouveaux coins est figé (forcé ou subi), par exemple celui en (n,p+1), la propagation de contrainte par rapport au coin opposé passe forcément par la cellule (n,p) ou (n-1,p+1), qui doit être aussi figée. Donc le treillis (n,p) ou (n-1,p+1) est intégralement rigide par hypothèse de récurrence. Et par propagation de contraintes, toutes les cellules de la colonne ou de la ligne supplémentaire le sont si la cellule (n,p+1) est figé. Le treillis (n,p+1) est intégralement rigide.
Puisque c’est vrai pour (n,1) et (1,2), c’est vrai pour (n,2). Puis pour (1,3) et donc (n,3),… donc pour (n,p)
Le test de rigidité par les coins opposés est donc suffisant pour savoir si un treillis est rigide ou pas.
Concernant le nombre minimum de cellules à rigidifier, on peut trouver un tas de solutions en rigidifiant uniquement n+p-1 cellules du treillis. Par exemple deux bords adjacents du treillis.
n+p-1 est le minimum pour (1,1), (1,2), (2,2). Imaginons que cette règle soit un minima jusqu’à un treillis (n,p-1). En ajoutant donc uniquement 1 cellule rigidifiée à chaque ajout d’une ligne ou d’une colonne.
Et imaginons qu’un treillis (n,p) soit le plus petit échappant à la règle (n+p-2 au maximum suffit). C’est-à-dire le même nombre que le minimum pour un treillis strictement plus petit. Cela signifie que l’ajout d’au moins une colonne a été gratuit, sans aucune cellule rigidifiée supplémentaire, puisque par récurrence de construction du treillis plus petit, on n’a ajouté qu’une cellule rigide par ligne ou colonne (pas de ‘gras’). Donc une colonne au moins de notre treillis (n,p) ne contient aucune cellule rigidifiée à priori. Donc aucune cellule rigide dans l’absolu, car la rigidité ‘subie’ ne peut être imposée uniquement par des colonnes adjacentes : mêmes si toutes les cellules des colonnes adjacentes sont intégralement figées, le cisaillement reste possible. De fait le treillis (n,p) ne peut être rigide.
Il faut donc à minima n+p-1 cellules rigidifiées pour un treillis (n,p)
#7 - 02-05-2020 16:55:17
- caduk
- Professionnel de Prise2Tete
- Enigmes résolues : 45
- Messages : 398
déforlation d'un treillis
gwen27
Spoiler : [Afficher le message]
Tu as bien la borne inférieure.
J'ai un doute sur ta démo. Pourquoi est ce toujours possible de trouver une ligne ou une colonne telle que si on l'enlève, le reste du treillis reste rigide?
#8 - 02-05-2020 17:59:21
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 6,193E+3
Déformation d'u treillis
Ca n'est pas obligatoirement possible justement.
Ce qui est sur, c'est que si le reste est rigide, alors, rajouter cette maille la rigidifie.
C'est un raisonnement un peu par l'absurde.
A chaque étape, je me dis que si le reste est rigide, alors cette maille l'est.
Si j'aboutis à une maille unique rigide, alors je peux reprendre le raisonnement à l'envers, et conclure que le treillis est rigide.
Sinon, c'est qu'à une des étapes ma supposition était fausse. Le treillis n'est pas rigide. Je pense que c'est plutôt sur cette réciproque que tu coinces.
#9 - 02-05-2020 18:56:19
- caduk
- Professionnel de Prise2Tete
- Enigmes résolues : 45
- Messages : 398
déformztion d'un treillis
gwen27
Spoiler : [Afficher le message] oui, ton raisonnement à l'envers me parait très suspicieux, si une propriété est vraie, cela ne nous dit rien sur sa réciproque. Qui te dis qu'il n'existe pas un treillis assez grand qui demande moins de m+n-1 cellules rigidifiées (et donc pour lequel en enlevant des colonnes ou lignes, on finirait forcément par tomber sur un treillis non rigide)
Ton raisonnement marcherait si on pouvait prouver que pour tout treillis rigide, il existe une colonne (ou ligne) tel que si on l'enlève, le treillis reste rigide. Cette propriété m'a l'air vraie, mais elle n'est pas forcément évidente à prouver...
Toufau
Spoiler : [Afficher le message] Désolé 
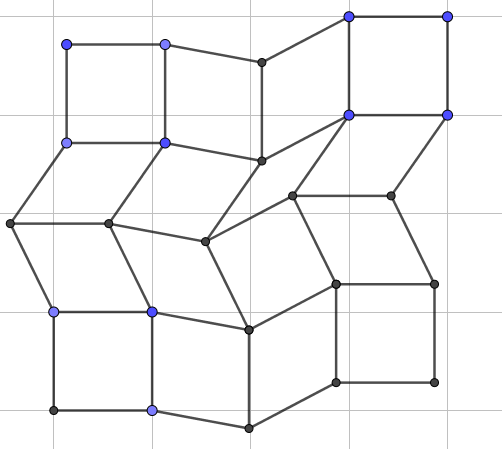
Les deux coins sont à la même position que si le treillis était tout carré (comme si on les scotchait à une table), avec les mêmes angles et tout, et on conserve une certaine liberté de mouvement. (même si il n'y a pas beaucoup de jeu...)
Quoi qu'il en soit, ton raisonnement par la suite me parait également sujet à failles, même si je ne suis pas trop entré dans les détails, à voir...
#10 - 02-05-2020 19:27:34
- TOUFAU
- Professionnel de Prise2Tete
- Enigmes résolues : 0
- Messages : 105
Déformation d'un treilli
Caduk,
peut être n'ai-je pas compris précisément ton énoncé.
Dans ma compréhension, ton exemple ne fige pas les coins opposés (bas gauche et haut droit). Rien n'empêche en effet celui par exemple en haut de se déplacer par rapport à celui en bas, par cisaillement. De fait le treillis n'est pas rigide.
Mon raisonnement fonctionne je pense si 'rigidifier une cellule=la contraindre à rester carrée' et 'figer deux cellules distinctes = les contraindre à l'immobilisme relatif entre elles'.
J'ai l'impression que tu exprimes qu'il existe un 'éther' derrière le treillis, qui fait que quand une cellule est rigidifiée elle ne peut plus se déplacer dans l'espace. Ce n'était pas mon hypothèse, je pensais que les cellules n'étaient tenues qu'entre elles et à rien d'autre.
#11 - 02-05-2020 19:42:25
- caduk
- Professionnel de Prise2Tete
- Enigmes résolues : 45
- Messages : 398
Déformatin d'un treillis
Toufau
Spoiler : [Afficher le message] Pardon, je n'avais pas compris que tu imposais ça pour les deux paires de coins opposés simultanément. Dans la définition de mon problème, les cellules ne sont pas figées dans l'espace, juste forcées à être carrée, par contre, de ce que j'ai compris dans ton post, tu forces les coins à la fois à être carrés, avec le même angle, et situé à la même distance que si le treillis était située dans sa forme carrée (ce qui revient au schéma que j'ai fait). Si tu impose seulement que les coins soient carrés et de mêmes angles, ça ne suffit pas à rigidifier le treillis...
#12 - 02-05-2020 20:15:53
- TOUFAU
- Professionnel de Prise2Tete
- Enigmes résolues : 0
- Messages : 105
Défformation d'un treillis
Caduk,
je n'ai pas été clair :-)
Dans mon raisonnement, je n'impose que la rigidité de certaines cellules choisies dans le treillis, pas plus. C'est-à-dire des cellules choisies individuellement et forcées en forme carré.
Je dis juste que la question de savoir si un treillis est totalement rigide revient à considérer que toutes ses cellules sont 'figées' les unes par rapport aux autres. donc plus de déplacement relatif entre elles (ni rotation). Si jusque là on est d'accord, mon raisonnement revient alors à chercher à démontrer que si deux coins opposés sont figés l'un vis à vis de l'autre (via des contraintes intermédiaires de cellules rigides bien sur), alors le treillis est totalement rigide. Je pense que je ne suis pas hyper clair (bon 43 jours de confinement aussi... j'ai des excuses :-))
#13 - 02-05-2020 23:53:41
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 6,193E+3
Déformation d'un trelilis
On va prendre la chose encore autrement.
Deux mailles rigides dans la même colonne fixent le parallélisme (vertical) de leurs lignes respectives, et inversement.
A partir d'une maille fixe, il faut fixer m-1 lignes et n-1 colonnes ce qui nécessite m+n-2 mailles rigides en plus.
Sinon, une ligne ou une colonne ne sera pas liée aux autres. Le réseau sera flexible.
#14 - 03-05-2020 16:59:56
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
Déformation d'un treilllis
Je ne suis pas sûr d'avoir compris la question : le treillis est formé de carrés mais sa forme globale est aussi un carré ?
Vasimolo
#15 - 03-05-2020 21:18:54
- caduk
- Professionnel de Prise2Tete
- Enigmes résolues : 45
- Messages : 398
Défoormation d'un treillis
Toufau
Spoiler : [Afficher le message] Ok, je comprend mieux ton raisonnement...
La démo à proprement dite de la minimalité est en fait seulement dans ton dernier paragraphe.
Tu semble supposer que le treillis rigide s'obtient en construisant récursivement un treillis sans cesse rigide. Mais qui te dis que tout les treillis rigides s'obtiennent comme ça? Si ça se trouve, en associant un treillis non rigide avec une colonne contenant case rigidifiée, il est possible d'obtenir un treillis rigide (et qui contient moins de n+p-1 cellules rigidifiées) D'ailleurs, on peut mettre une case rigidifiée pour chaque ligne et colonnes avec moins de n+p-1 cellules rigidifiées (en complétant la diagonale (même si le treillis n'est dans ce cas pas rigide)
gwen27
Spoiler : [Afficher le message] Tu as l'idée principale. Si je chipote un peu, tu ne démontres pas vraiment que si une ligne n'est pas liée aux autres, alors il y a déformation possible. (mais bon, je chipote)
Vasimolo
Les cellules sont initialement carrées, mais peuvent devenir des losanges une fois déformées. Le treillis lui même peut être un carré ou un rectangle (ou encore autre chose, genre une croix) mais ça ne modifie pas notablement la résolution.
#16 - 03-05-2020 23:36:04
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 6,193E+3
féformation d'un treillis
Si on imagine ce treillis carré, une maille libre peut évidemment être mobile.
#17 - 04-05-2020 08:18:06
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
déformation d'ub treillis
Considérons par exemple un rectangle de longueur C et de largeur L . On peut remarquer que chaque petit carré rigidifié va bloquer les directions de toutes les lignes de sa colonne et de toutes les colonnes de sa ligne . On peut constituer un graphe biparti dont les sommets sont les lignes et les colonnes du rectangle , les arêtes représentant les carrés rigides . On note que chaque petit carré est bloqué si et seulement si sa ligne et sa colonne sont dans la même composante connexe du graphe . Le treillis est bloqué lorsque toutes les petits carrés sont bloquées c’est-à-dire lorsque le graphe est connexe . Il faut donc au moins L+C-1 arêtes pour bloquer le rectangle . La réalisation d’un graphe connexe avec L+C—1 arêtes ne pose pas de problème .
Vasimolo
#18 - 04-05-2020 10:30:45
- caduk
- Professionnel de Prise2Tete
- Enigmes résolues : 45
- Messages : 398
déformatiob d'un treillis
gwen27
Spoiler : [Afficher le message]
"Si on imagine ce treillis carré, une maille libre peut évidemment être mobile."
Pourquoi, ca ne me parait pas si évident.
Si pour toi, une maille est une ligne ou une colonne, alors si une ligne (ou une colonne) ne contient aucune case rigidifiée, clairement le treillis est mobile.
Si une maille est ce que j'appelle une cellule, ça ne me parait pas si évident, il peut y avoir d'autre processus géométriques qui la rendent rigides (ou alors j'ai loupé ta démo sur ce point)
Tu décris un processus de construction qui donne un treillis rigide (et je suis ok avec ça). Cependant tu ne montres pas que ce procédé génère toutes les treillis rigides possibles. Si l'on ne suit pas ton processus de construction, on peut trouver un treillis avec une cellule rigidifiée par ligne et colonne avec moins de m+n-1 cellules rigidifiée. Et peut être que ce treillis est rigide, par d'autres phénomènes géométriques que celui que tu as décris.
Vasimolo
Spoiler : [Afficher le message] Même remarque que pour gwen27, tu as le bon raisonnement pour résoudre le problème, mais tu ne démontres pas que ton processus est le seul à pouvoir rigidifier le treillis, à moins que tu ne justifies proprement ça :
"On note que chaque petit carré est bloqué si et seulement si sa ligne et sa colonne sont dans la même composante connexe du graphe."
Car ça ne me parait pas si évident...
#19 - 04-05-2020 10:44:39
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3839
Déformation d'u ntreillis
Pour rigidifier un treillis, il faut au moins trouver 3 cases en L voisines par les cotés. Le rectangle circonscrit est alors frigide ( euh rigide je voulais dire). Ensuite, il faut trouver au moins 1 case rigide voisine par 1 coté à ce rectangle. On forme alors un nouveau rectangle rigide circonscrit plus grand qui contient cette nouvelle case, auquel il faudra trouver au moins 1 nouvelle case rigide voisine par un coté, et on agrandit à nouveau le rectangle circonscrit, etc....
Au total, pour un treillis compliqué formé d'une multitude de rectangles collés, il faut au moins 1 rectangle rigidifié par sa longueur et sa largeur, soit L+l-1 cases rigides. Ensuite, pour tous les rectangles collés, on devra rigidifier le coté perpendiculaire au coté collé au rectangle précédent, soit une case par unité de longueur de ce coté.
Ce qui est remarquable, c'est qu'on n'a besoin que de 3 cases rigidifiées voisines par le coté pour rigidifier un treillis complet, si compliqué soit il ( à condition que les rectangles aient une largeur supérieure à l'unité ).
#20 - 05-05-2020 00:25:29
- caduk
- Professionnel de Prise2Tete
- Enigmes résolues : 45
- Messages : 398
déformatiin d'un treillis
nodgim
Spoiler : [Afficher le message] Oulah, j'ai du mal à suivre... Tu sembles dire que l'on peut rigidifier un rectangle avec L+l-1 cases rigides. C'est vrai, mais est ce le minimum?
"Pour rigidifier un treillis, il faut au moins trouver 3 cases en L voisines par les cotés" Euh, non, pas forcément, par exemple, sur un treillis 3x3, on peut rigidifier comme ça:
XOX
OOX
XXO
où X est une case rigide.
Je ne comprends pas très bien la suite... 
#21 - 05-05-2020 11:45:18
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
déformation s'un treillis
« Chaque petit carré est bloqué si et seulement si sa ligne et sa colonne sont dans la même composante connexe du graphe »
Ca me semblait clair avec l’explication du « blocage des directions mais je suis d’accord avec toi , la réciproque n’est pas évidente .
Le sens direct est clair , par exemple si on a le chemin L2>C3>L4>C6 , c’est-à-dire que les carrés L2C3 , L4C3 et L4C6 sont rigidifiés avec des baguettes alors toutes les tiges « verticales » de la ligne L2 sont parallèles ainsi que celles de L4 . De même pour toutes les tiges « horizontales » des colonnes C3 et C6 . La case L2C6 a ses côtés » horizontaux » parallèles à ceux de L4C6 et ses côtés « verticaux » parallèles à ceux de L2C3 , la présence du carré L4C3 entraîne que L2C6 est aussi un carré . On procède de même pour un chemin plus long .
La réciproque est presqu’aussi évidente mais assez pénible à expliquer il suffirait de construire le treillis en gardant les bonnes directions pour toutes les composantes connexes et choisir les autres en évitant les angles droits .
Vasimolo
#22 - 05-05-2020 12:24:53
- caduk
- Professionnel de Prise2Tete
- Enigmes résolues : 45
- Messages : 398
déformation d'un treimlis
Vasimolo
Il y a un moyen de montrer la réciproque de manière pas trop pénible (c'est à dire le treillis peut se tordre s'il ne vérifie pas les conditions que tu énonces)
Indice :
Spoiler : [Afficher le message] construire un damier
#23 - 06-05-2020 10:45:43
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3839
défotmation d'un treillis
Peux tu ajouter du temps, 72 heures par exemple ?
J'ai regardé ce problème très tardivement, je me rends compte que je n'ai pas fait le tour.
Merci d'avance.
#24 - 06-05-2020 18:30:30
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3839
déformation d'ub treillis
Merci pour le temps ajouté !
Une 1ère version, j'espère qu'elle est assez claire.
------------------------------------------------------------------------
La caractéristique d’un tel treillis souple est que pour une ligne donnée, les barres verticales sont inclinables mais s’inclinent toutes en même temps selon la même angulation, elles restent parallèles. Idem pour les barres horizontales d’une même colonne.
Le fait de rendre une cellule rigide n’a qu’une seule incidence : l’inclinaison de la cellule est identique, au 1/4 de tour près, pour les barres de sa ligne et les barres de sa colonne.
Le fait de rendre rigide 3 cellules formant 3 sommets d’un même rectangle rend la cellule du 4ème sommet rigide de fait, par le jeu des parallélismes croisés. On peut dire que ces cellules forment un réseau, du fait que l’inclinaison de l’une quelconque de ces cellules conduit à l’inclinaison identique des 3 autres.
Le réseau est extensible par ajout d’une cellule rigide sur l’une des 4 lignes + colonnes de ce réseau : si la cellule rigide supplémentaire est installée sur une des 2 lignes, la colonne correspondante fait alors partie du réseau, et la cellule au croisement de cette colonne et de la seconde ligne du rectangle devient alors rigide de fait. Idem pour une cellule supplémentaire sur une des 2 colonnes.
0201000
0000000
0101000
Ici la cellule 2 est rigidifiée par les 3 cellules rigides 1.
0201000
0103000
0101000
L’ajout d’une cellule rigide (1) sur la ligne 2 rend la cellule 3 elle même rigide
De proche en proche, on rigidifie toute une trame de cette façon, c’est à dire en ajoutant une cellule rigide sur une ligne ou une colonne du réseau ainsi formé. En comptant bien, si avec les 3 cellules initiales, on forme un réseau de 4 lignes + colonnes, toute cellule rigide ajoutée à ce réseau ajoute une ligne ou une colonne à ce réseau. Pour rigidifier un réseau complet de n lignes et m colonnes, n+m-1 cellules rigides sont nécessaires et suffisantes.
On pourrait construire sur un treillis donné, au lieu d’un seul réseau, 2 réseaux ou davantage.
Chaque réseau aurait ses lignes et colonnes propres ( d’après la description faite ci-dessus, une ligne ou une colonne ne peut appartenir qu’à un seul réseau ). Mais malheureusement le treillis ne sera pas rigide : on pourra toujours incliner les cellules rigides d’un réseau indépendamment du reste du treillis.
Voici le montage d’un treillis 5*5 à 2 réseaux ( cellules 1 pour réseau 1, cellules 2 pour réseau 2)
10010
02202
10000
10010
02202
Au réseau 1 : lignes 1 2 et 3 , colonnes 1 et 4
Au réseau 2 : lignes 2 et 5, colonnes 2,3 et 5.
On notera qu’avec 11 cellules rigides, malgré toutes les lignes et toutes les colonnes occupées par au moins 1 cellule rigide, le treillis n’est pas rigide. On ne peut pas rendre compte de la rigidité d’un treillis par le seul décompte du nombre de cellules rigides. On pourrait rendre rigide la moitié des cellules de chaque ligne ou chaque colonne d’un treillis sans que celui-ci soit rigide pour autant ( cellules rigides des cases blanches d’un damier par exemple).
Il n’est donc pas facile de reconnaître un treillis rigide, il faut identifier l’amorce d’un réseau et vérifier que toutes les colonnes et les lignes en font partie.
#25 - 06-05-2020 19:01:13
- caduk
- Professionnel de Prise2Tete
- Enigmes résolues : 45
- Messages : 398
Déformatio nd'un treillis
nodgim
Ok pour la construction du treillis rigide.
Pareil que pour Vasimolo et gwen27, tu as la bonne construction, reste à prouver que si le treillis ne respecte pas la construction, alors le treillis n'est pas rigide.
|
 |

 Accueil
Accueil
 Forum
Forum








