Forum dédié aux énigmes et à toutes formes de jeux de logique. | Déconnexion |
|
Tu n'es pas identifié sur Prise2tete : s'identifier.  Accueil Accueil
 Forum Forum
|
 |
#1 - 21-06-2021 16:37:52
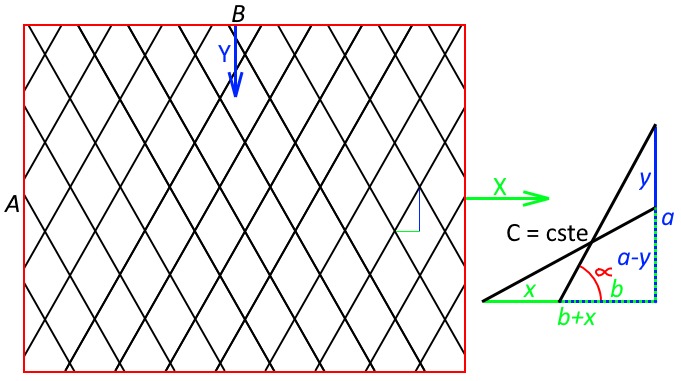
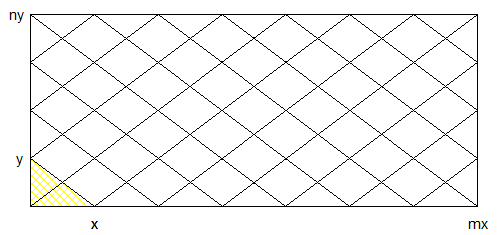
uis perdu sur l'océanje pars d'un rectangle de a X b si j'étends b de x que devient a.
#0 Pub#2 - 21-06-2021 23:12:49
Suis perdu sur ll'océanBen là à vu de nez je dirais que si ton a X b = S (S est la surface) #3 - 23-06-2021 17:09:31
duis perdu sur l'océanBonjour solavain #4 - 23-06-2021 21:25:15
Sus perdu sur l'océanQue c'est mignon présenté comme ça #5 - 24-06-2021 17:09:36
Suis perdu sur l'océéanFort bien, scarta. #6 - 26-06-2021 09:48:30
Suis perdu sur l'océa(a-y)² = (b+x)² => y = a.[1 - V(1-(x/a)²-(2.b.x/a)²)] #7 - 26-06-2021 21:35:30
Suis perdu sur 'locéanFranky : je pense que ton "b=x" signifie "b+x", mais ton égalité : #8 - 27-06-2021 12:28:36
suis perdu sur l'oxéanBonjour à tous Réponse rapideSujets similaires
|
 | ||||||||||||||||||||||||||||||
| Prise2Tete Forum Statistiques Liste des membres Hall of Fame Contact | ||||||||||||||||||||||||||||||||
Un jeu où seules la réflexion, la logique et la déduction permettent de trouver la solution.