 |
#1 - 11-11-2025 19:56:53
- w9Lyl6n
- Professionnel de Prise2Tete
- Enigmes résolues : 26
- Messages : 239
La quête de l'évasive spirale d'rO
Fiorino apprenti du célèbre mathématicien Fibonacci a toujours eu une fascination pour le nombre d'or. Ainsi il a payé un chaudronnier pour lui confectionner un plateau métallique rectangulaire, dont le rapport de la grande largeur sur la petite est le nombre d'or, et il prie chaque soir sa mère de bien vouloir confectionner dessus une fougasse (la pizza n'ayant pas encore été inventé à cette époque, faute de tomates cultivées en Europe).
Un dimanche, ayant invité son maître à dîner chez lui, il lui présente une fougasse sur le fameux plateau. Fibonacci fait alors remarquer qu'en découpant dans un coin deux petits carrés de côté approximativement la petite largeur du plateau divisé par un des nombres de sa suite (qui porte aujourd'hui son nom) assez grand de préférence, on peut facilement en démarrant dans la bonne direction découper des carrés aussi parfait qu'il puisse être conçu par l'oeil humain, de plus en plus gros, qui finiront par recouvrir parfaitement le plateau. Et comme démonstration il exécute la découpe (ci-dessous sur la figure de gauche), sans l'aide d'aucun instrument autre qu'un couteau et son habileté à diviser assez bien à l'oeil une longueur en deux.
Fiorino, épaté par la performance de son maître, décide dès le lendemain d'améliorer la technique de Fibonacci afin de l'impressionner le dimanche suivant. Son idée est de disposer les carrés en spirale. Mais comme il est délicat de placer les deux petits carrés au centre de la fougasse, il commence par le grand carré dont le côté prend toute la petite largeur du plateau, et procède à l'aide d'un compas de marine très précis en reportant les longueurs des petits côtés des rectangles restant à chaque étape pour former les carrés successifs. Le chaudronnier ayant fait un travail impeccable sur le plateau métallique, il espère aboutir à une spirale parfaite avec des carrés aussi petit que la lame de son couteau lui permette de découper. Las ! Malgré tout le soin qu'il apporte à sa découpe, il abouti rapidement à un petit rectangle mal dimensionné bien avant que l'épaisseur de sa lame puisse sans mauvaise fois être incriminée. Ses tentatives les soirs suivant ne sont pas plus fructueuses, à son grand désarroi.
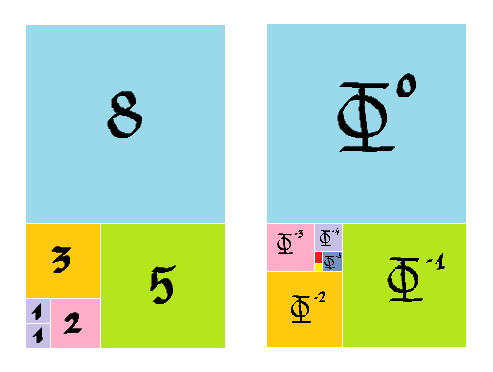
Quelle est donc cette malédiction qui fait échapper la spirale d'or à Fiorino ?
Comment peut-il améliorer sa technique de découpe pour réaliser la spirale d’or ?
Parviendra-t-il à découper la fougasse sur son plateau en une spirale d’or convaincante, armé uniquement de son couteau et en gardant les parts intactes ? (les parts carrés peuvent être marquées superficiellement mais sans jamais traverser la fougasse)
Bonne chance dans votre quête et bon appétit !
#2 - 12-11-2025 12:06:28
- Migou
- Expert de Prise2Tete
- Enigmes résolues : 17
- Messages : 888
- Lieu: Ville 2/N près 2*i
la quête de l'évasive spurale d'or
Hum,
je dirais que le ratio des côtés de la n'est pas le même à chaque pas de la spirale.
Par conséquent, lorsqu'on choisit la valeur du petit côté du plateau, il faut la choisir pour que le ratio soit respecté.
exemple
Si l'on décude de graduer le petit côté du plateau en 8 unités.
13/8 = 1,625
c'est donc le ratio des côtés du plateau de Fiorino.
s'il décide de graduer en 13 :
21/13 = 1,165...
Il faudrait construire un plateau d'un rapport différent et les deux plateaux ne seront pas superposables.
#3 - 12-11-2025 12:38:53
- w9Lyl6n
- Professionnel de Prise2Tete
- Enigmes résolues : 26
- Messages : 239
la quête de l'évasivr spirale d'or
Migou: On considère comme expliqué que le plateau a bel et bien un ratio grand sur petit coté égale au nombre d'or (ou aussi proche qu'il est nécessaire de l'être du nombre d'or, pour être réaliste)Spoiler : [Afficher le message] , c'est donc le découpage de Fibonacci qui n'est pas mathématiquement parfaite, pourtant cela ne se voit pas. À l'inverse le plateau est parfait pour découper une spirale d'or avec théoriquement une infinité de carrés, pourtant cela s'avère très difficile, on voit bien que la spirale s'interrompt avec un rectangle disgracieux. Pourquoi ?
Je précise que la forme et le nombre d'itération avant d'obtenir ce triangle disgracieux varie, c'est bien un problème d'imprécision de la construction très difficile à surmonter avec la méthode de Fiorino.
Je te suggère d'essayer de dessiner la spirale à la règle et au compas pour te rendre compte par toi même !
#4 - 12-11-2025 19:19:53
- aunryz
- Elite de Prise2Tete
- Enigmes résolues : 17
- Messages : 1414
- Lieu: Nicastro / Tronville
L aquête de l'évasive spirale d'Or
La technique de Fiorino avec ses reports successifs, à partir du grand carré, est très sensible aux erreurs qui même très minimes, auront de plus en plus d'importance en allant ainsi du plus grand au plus petit.
Et l'erreur elle même n'a aucune régularité.
Il ferait mieux de choisir la taille de son petit carré et décider de faire par exemple 8 étapes dans sa spirale, il peut alors déterminer la position de ce petit carré. et partant de là les erreurs qu'il pourra faire seront minimes et de plus en plus négligeables (ajustement possibles peu visibles).
(me suis surement planté quelque part, mais ...)

*Pour 8 étapes, sommet en bas à gauche de coordonnées (9;5) second carré à sa droite. (j'ai mis le plateau dans l'autre sens)
Lélio Lacaille - Du fagot des Nombreux
#5 - 12-11-2025 20:02:42
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 6,192E+3
La quête de l'éévasive spirale d'Or
S'il est précis, je ne vois pas le souci, même si le compas doit vite devenir hasardeux.
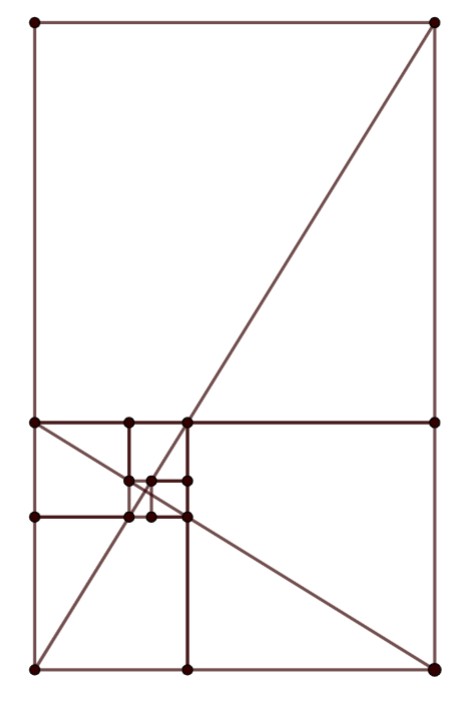
Par contre, en traçant les deux diagonales des deux premiers rectangles, il peut y aller à la louche ensuite.
#6 - 13-11-2025 11:49:56
- w9Lyl6n
- Professionnel de Prise2Tete
- Enigmes résolues : 26
- Messages : 239
La quête de lévasive spirale d'Or
aunryz: Oui c'est l'idée ! Serais tu quantifier ? Par contre partir de petits carrés semble hasardeux, comment trouver où démarrer dans le rectangle et construire des carrés de la bonne taille avec les outils dont il dispose ?
gwen27: Bravo Tu as parfaitement répondu à la dernière question ! Par contre non, il y a un autre soucis avec la méthode de Fiorino que celui que tu décris
#7 - 13-11-2025 22:02:47
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 6,192E+3
la quête de m'évasive spirale d'or
Avec cette méthode, la perte de précision ne sera pas amplifiée de tracé en tracé, on se ramènera toujours aux deux lignes de base, voire même un tracé va rattraper une erreur sur le précédent.
Avec sa méthode, les erreurs s'accumulent.
#8 - 14-11-2025 09:26:41
- dylasse
- Professionnel de Prise2Tete
- Enigmes résolues : 21
- Messages : 381
La quête de l'évasive sppirale d'Or
L'escroc est Fibonacci : sa dernière part n'est pas un carré car Phi n'est pas égal à 13/8. Précisément, s'il a choisi comme sur le dessin, une unité de base étant un huitième de la largeur, sa dernière part aura un coté de 8 et un coté égale à Phi x 8 - 5 = 7,94, soit "presque" un carré.
Fiorino, avec sa méthode aura toujours un "reste" (après avoir ôté un carré) étant un rectangle d'or qu'il ne pourra pas découper en 2 carrés égaux.
Fiorino n'a rien à modifier à sa découpe, mais il doit accepter que son découpage est infini.
S'il veut vraiment copier son maître, il doit d'abord décider de la dimension du carré unité final ce qui déterminera le rang n dans la suite de Fibo du dernier carré puis "tricher" sur la première découpe (là où le défaut est le moins visible) pour se ramener après la première coupe à un rectangle de rapport Un / Un+1 et non plus Phi. Une subtilité réside dans le fait que la parité de n implique qu'il découpe une premier carré avec une "hauteur" plus petite que la "base" si n est impair (comme pour l'exemple de l'énoncé avec n=5) ou plus grande si n est impair, le rapport Un+1/Un étant alternativement au dessus ou en dessous de Phi (par exemple pour n=2, la première part devrait être un "faux carré" de 2 x 2,23, ce qui est le pire cas).
#9 - 14-11-2025 11:54:07
- w9Lyl6n
- Professionnel de Prise2Tete
- Enigmes résolues : 26
- Messages : 239
La quête de 'évasive spirale d'Or
dylasse : Tous cela est parfaitement juste, mais ce n'est pas le problème de Fiorino, il est bien conscient que sa spirale est infini, mais espère tout de même poursuivre « avec des carrés aussi petits que la lame de son couteau lui permette de découper ». Or comme illustré sur le dessin on voit que le dernier rectangle en rouge est plus grand que le dernier carré en jaune, ce qui devrait être impossible. Sa découpe a des petites imprécisions inévitables à chaque étape et cela aboutit rapidement à quelque chose de suffisamment faux pour que ce n'ait plus aucun sens de poursuivre.
Indice à tous et toutes : Spoiler : [Afficher le message] Pour commencer regarder ce qui se passe dans chaque cas si à la première découpe on fait une imprécision de "epsilon" et que toutes les découpes suivantes sont mathématiquement parfaites
#10 - 14-11-2025 12:14:06
- aunryz
- Elite de Prise2Tete
- Enigmes résolues : 17
- Messages : 1414
- Lieu: Nicastro / Tronville
La quêête de l'évasive spirale d'Or
En réponse à ton indice, c'est ce que j'ai évoqué dans ma réponse, "auront de plus en plus d'importance en allant ainsi du plus grand au plus petit."
Je précise "Comme les tailles des carrés diminuent géométriquement (facteur 1/φ ≈ 0,618 à chaque fois), les erreurs relatives s'amplifient rapidement sur les petites échelles."
Sinon, ... lorsqu'on a décidé de la taille du petit carré, on peut le situer (ici 1/34 de la longueur)
Une piste ...
on triche un peu en utilisant la propriété de 36 (sourire)²
Lélio Lacaille - Du fagot des Nombreux
#11 - 14-11-2025 16:39:13
- w9Lyl6n
- Professionnel de Prise2Tete
- Enigmes résolues : 26
- Messages : 239
Laa quête de l'évasive spirale d'Or
Spoiler : [Afficher le message] L'imprécision est pire que ce que vous croyez, il y a bien quelque chose à creuser de non trivial. Pour s'en rendre compte il faut soit faire les calculs, soit essayer soi même de dessiner la figure.
Illustration :
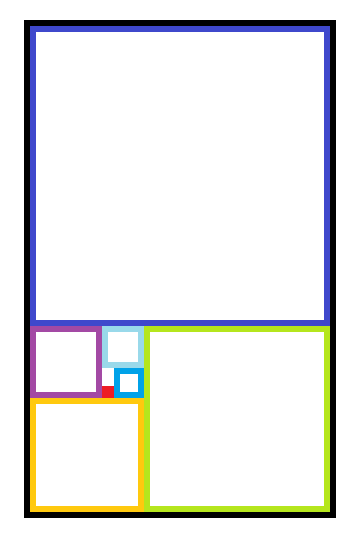
L'intérieur du rectangle aux bords noir ci dessous fait exactement 81×50 pixels, soit initialement moins d'un dixième de pixel d'erreur par rapport à un rectangle d'or parfait.
Pourtant après 6 itération avec des carrés parfaits (nombre entier de pixels), le rectangle restant au lieu de faire environ 1,236×2 pixels, fait en fait 3×2 pixels, soit une erreur initiale amplifiée plus de 17 fois par rapport à la situation parfaite.
Notez bien que ce n'est pas un problème de grille de pixel. La grille de pixel est juste là pour s'assurer que les carrés sont parfaits. On peut imaginer la même situation avec un rectangle initiale parfait, et une erreur sur le 1er carré où il manquerait environ 1/500 de sa hauteur, on en serait rendu exactement au même point...
#12 - 15-11-2025 15:40:44
- aunryz
- Elite de Prise2Tete
- Enigmes résolues : 17
- Messages : 1414
- Lieu: Nicastro / Tronville
la quête de l'écasive spirale d'or
Si la première découpe est en bleu, trois coups de couteaux (ou de feutre) sont inutiles.
Etc...
N'est-il pas ?
Lélio Lacaille - Du fagot des Nombreux
#13 - 15-11-2025 23:28:50
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 6,192E+3
la quête de l'évasibe spirale d'or
Tu as faux car tu considères l'imprécision initiale, puis des découpes parfaites ce qui donne une progression arithmétique de cette imprécision.
L'erreur de découpe a autant de chance de se faire en positif qu'en négatif.
Globalement, si le rectangle initial est parfait, tu as tort.
Avec ton exemple assumant une approximation dès le départ, tu as raison.
#14 - 16-11-2025 12:17:16
- w9Lyl6n
- Professionnel de Prise2Tete
- Enigmes résolues : 26
- Messages : 239
la quête de l'évasive spirale d'oe
auryz : je n'ai pas dessiné des découpes en couleur mais les bords des carrés avec une épaisseur d'un pixel à l'intérieur des carrés.
gwen27 : dans mon indice j'ai bien précisé que considérer une imprécision uniquement au début c'était "pour commencer", ça permet de comprendre l'effet qui se produit sans entrer dans trop de calculs (j'ai également décrit une situation similaire où le rectangle initiale est parfait et c'est le 1er carré qui est imparfait).
Le cas qui nous intéresse n'est absolument pas celui de la perfection mais celui où il y a des petites imprécisions à chaque découpe. Quand tu dis « L'erreur de découpe a autant de chance de se faire en positif qu'en négatif » est ce que tu fais la conjecture que les erreurs en positif interfèrent avec celles en négatif au file des découpes et que cela suffit pour changer le comportement global de l'erreur ? Si c'est bien ça ton intuition, fait les calculs, tu verras que ce n'est pas le cas (la formule finale est plutôt élégante, c'est très satisfaisant de travailler avec le nombre d'or). Un système instable ne se corrige pas avec des petites corrections aléatoires.
#15 - 16-11-2025 18:51:00
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 6,192E+3
La quête de l'évasvie spirale d'Or
Je suis tout à fait d'accord, mais dans une énigme, quantifier le hasard est ... hasardeux.
Il a de bonnes chances de s'en tirer, compte tenu des limites du couteau, en un nombre assez retreint d'essais.
Plus on part d'un TTTTTRRRrrrèèès grand gâteau, moins il a de chances, c'est indiscutable.
Tu parles dans le même message de calculs précis et de découpes imprécises.
#16 - 19-11-2025 23:05:07
- w9Lyl6n
- Professionnel de Prise2Tete
- Enigmes résolues : 26
- Messages : 239
la quête de l'évasive spirale d'pr
Je regrette que personne n'ait essayé de modéliser le phénomène par le calcul, car là réside la beauté de cette énigme, c’est tellement beau que je pense en faire un tiktok oddly satisfying. En tout cas j'espère vous en persuader vous, avec la solution que je vous propose ci dessous  : :
I. commençons comme proposé dans l'indice par imaginer qu'une seule imprécision initiale est commise.
Dans cette situation si on note [latex]u_n[/latex] la longueur du petit côté du rectangle à la nième découpe relative à celui du rectangle initiale, on a alors deux termes de la suite fixés et une relation de récurrence :
> Dans le cas de la découpe de Fibonacci :
[TeX]u_0 = 1[/TeX]
[TeX]u_1 = 1 + Err[/TeX]
[TeX]u_{n+2} = u_{n+1} + u_n[/TeX]
> Dans le cas de la spirale de Fiorino :
[TeX]u_0 = 1[/TeX]
[TeX]u_{-1} = \frac{1}{\Phi} + Err[/TeX]
[TeX]u_{-(n+2)} = u_{-n} - u_{-(n+1)}[/TeX]
Note : J'utilise à dessin une suite récurrente avec des termes qui descendent vers les négatif de manière à pouvoir réorganiser les termes en [latex]u_{-n} = u_{-n-2} + u_{-n-1}[/latex] ce qui est exactement la même relation de récurrence que pour la découpe de Fibonacci
La méthode de résolution d'une suite récurrente linéaire est bien connue, pour notre cas les solutions sont de la forme, admirez la symétrie :
[TeX]u_n = a\Phi^n + b(-\Phi)^{-n}[/TeX]
où [latex]a[/latex] et [latex]b[/latex] sont des coefficients qui sont déterminés en fixant 2 termes de la suite.
Ainsi si on pose [latex]\epsilon[/latex] un terme représentant une petite erreur :
Cas Fibonacci :
[TeX]u_n = \frac{\Phi + \epsilon}{\sqrt{5}} \Phi^n + \frac{-\Phi^{-1} - \epsilon}{\sqrt{5}}(-\Phi)^{-n}[/TeX]
Le terme d'erreur dominant est de l'ordre de [latex]\epsilon\Phi^n[/latex], il augmente de manière exponentielle ce qui pourrait apparaître dramatique, mais d'une part il conserve la même proportion que dans l'erreur initiale relative au côté de son rectangle, d'autre part [latex]\frac{u_{n+1}}{u_n}[/latex] converge toujours vers [latex]\Phi[/latex] donc la forme du rectangle final tend toujours vers un rectangle d'or.
Cas Fiorino :
[TeX]u_{-n} = (1 - \epsilon)\Phi^{-n} + \epsilon(-\Phi)^n[/TeX]
Le terme d'erreur dominant est [latex]\epsilon(-\Phi)^n[/latex], il augmente de manière exponentielle avec une alternance de signe, ce qui est particulièrement pathologique car la suite devrait être exponentiellement décroissante en amplitude ! Ainsi relativement à la spirale "parfaite" de formule [latex]\Phi^{-n}[/latex], la proportion de l'erreur augmente en [latex]\Phi^{2n}[/latex], soit plus de 100× d’augmentation d'erreur relative au côté en 5 itérations ! Et pour ne rien arranger les erreurs de deux termes consécutifs sont de signes opposées ce qui empêche de "masquer" l'erreur et augmente encore la déformation du rectangle !
II. Maintenant le cas général :
J'expliciterai seulement le cas de la spirale de Fiorino dans les grandes lignes.
On peut modéliser les découpes avec :
[TeX]u_{n+2} = u_n - u_{n+1} + \epsilon_{n+1} ~~~(*)[/TeX]
Où les [latex]\epsilon_n[/latex] sont les erreurs à chaque découpe, représentées par des variables aléatoires de moyenne 0 indépendante entre elles et de même écart type [latex]\epsilon[/latex].
Si on déroule la récurrence (*) on obtient quelque chose de la forme :
[TeX]u_{n} = A u_0 + B u_1 - \sum_{k=1}^{n}{F_k (-1)^k \epsilon_{n-k}}[/TeX]
où A et B sont exactement les mêmes coefficients que si il n'y avait pas de terme d'erreur. On en déduit donc que :
[TeX]u_{n} = \Phi^{-n} - \sum_{k=1}^{n}{F_k (-1)^k \epsilon_{n-k}}[/TeX]
En substituant dans la relation de récurrence (*) puis en identifiant les termes deux à deux grâce aux termes [latex]\epsilon_k[/latex] on trouve la nouvelle relation de récurrence :
[TeX]F_{n+2} = F_{n+1} + F_n[/TeX]
avec :
[TeX]F_1 = F_2 = 1[/TeX]
Tiens tiens, ça rappelle quelque chose non ? Le symbole F ne serait-il par particulièrement bien choisi ?  En effet les coefficients devant les erreurs ne sont autres que la suite de Fibonacci elle même ! Ainsi : En effet les coefficients devant les erreurs ne sont autres que la suite de Fibonacci elle même ! Ainsi :
[TeX]F_n = \frac{\Phi^n - (-\Phi)^{-n}}{\sqrt{5}}[/TeX]
On peut maintenant calculer la variance de l'erreur cumulée:
[TeX]V_n = E \left ( \left (\sum_{k=1}^{n}{F_k (-1)^k \epsilon_{n-k}} \right )^2 \right ) - 0^2[/TeX]
En se rappelant que les erreurs sont indépendantes et de moyenne nulle et après plusieurs simplifications particulièrement satisfaisantes  , on obtient : , on obtient :
[TeX]V_n = \frac{\Phi^{2n+1} - \Phi^{-2n-1} - (-1)^n}{5} × \epsilon^2[/TeX]
Et pour finir :
[TeX]\sigma_n = \sqrt{V_n} = \sqrt{\frac{\Phi^{2n+1} - \Phi^{-2n-1} - (-1)^n}{5}} × \epsilon[/TeX]
Si de plus on modélise les erreurs par une gaussienne, alors l'erreur cumulée est elle aussi une gaussienne parfaite dont l'écart type est donné ci-dessus.
Maintenant si on considère le terme dominant, l'ordre de grandeur de l'amplitude de l'erreur cumulée est exactement le même que précédemment quand on avait une seule erreur initiale, pour être précis il est maintenant de [latex]\sqrt{\frac{\Phi}{5}} \Phi^n \epsilon[/latex]
On note que étudier le cas simple a permis de mettre en évidence le caractère oscillant de l'erreur, ce qu'on ne peut pas voir ici puisqu'on travaille avec des écarts types.
Application numérique :
Imaginons que la lame du couteau de Fiorino fait 1mm d'épaisseur et que le petit côté du plateau fait 30cm. L’erreur type serait ainsi de 1/2 mm à chaque découpe.
L’erreur cumulé relative est alors de l’ordre de 80 % au bout de 7 découpes, pour un petit côté du rectangle qui aurait dû faire environ 1cm. En se rappelant que les erreurs cumulées et amplifiées oscillent, le dernier rectangle est très probablement extrêmement déformé alors qu'il est encore clairement visible !
III. La méthode « sans erreur visible »
Pour s’en sortir il suffit à Fiorino de tracer au couteau les diagonales des deux premiers rectangles, reportez-vous à la première réponse de gwen27 pour le jolie graphique 
Remarque : Fiorino peut utiliser le côté du plateau pour construire le premier carré et se passer totalement de compas !
Pourquoi ça marche beaucoup mieux :
La différence fondamentale c'est qu'on n'essaie pas de dessiner des carrés du mieux qu'on peut, mais des rectangles d'or : tout rectangle partageant une diagonale d'un rectangle d'or et ayant les côtés parallèles à ce même rectangle est un rectangle d'or. Ainsi on corrige au fur et à mesure les erreurs de proportion des rectangles.
Pour finir on obtient des carrés assez convaincants, non pas parce qu'on a cherché à construire des carrés directement, mais par les propriétés des rectangles d'or imbriqués.

|
 |

 Accueil
Accueil
 Forum
Forum










