 |
#1 - 21-06-2010 20:05:04
- McFlambi
- Professionnel de Prise2Tete
- Enigmes résolues : 48
- Messages : 144
Escalier et chaeaux
(je ne suis pas sur que cette énigme ou une équivalente ait été postée avant, j'ai cherché un peu et rien trouvé alors je la lance)
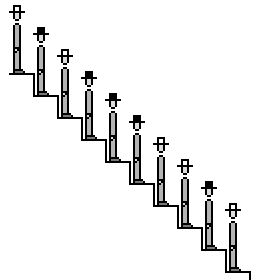
10 hommes sont réunis dans une salle où on leur annonce ce qui va leur arriver. Après quoi ils pourront choisir une stratégie avant de subir l'épreuve :
Ils seront placés chacun sur une marche d'un escalier (de 10 marches), face vers le bas de l'escalier (de manière à ne voir que ceux devant soi), et on placera un chapeau de couleur noire ou blanche sur chacune de leur tete (On ne peut pas voir la couleur de son propre chapeau, ni ceux derrière soi). Chacun, à son tour, en partant du plus haut (celui derrière tous les autres), devra crier haut et fort soit "Noir", soit "blanc". Si c'est la couleur de son chapeau, tout va bien. Sinon, tous sont éxécutés. Comme on est sympa, ils ont droit à 1 erreur. Comment s'en sortir ?
#2 - 21-06-2010 20:44:22
Escaleir et chapeaux
il y a combien de blanc et combien de noir ou si l image correspond a l enigme alors
1er dit blanc parce qu il ne voit que 4blanc
2 dit noir car il ne voit que 4 noir et 4 blanc mais celui de tout en haut a dit blanc
3 dit blanc car il e voit que 3 blanc et 4 noir mais ceux d enhaut on dit leur couleur
4 dit noir car il ne voit que 3noir
5 dit noir car il ne voit plus que 2 noir
6 dit noir car il ne voit plus qu'1 noir
7 dit blanc car il ne voit plus que 2 blanc
8 dit blanc car il ne voit pllus q'1 noir et q'1 blanc
9 dit noir car il a entendu 4 fois noir et voit un blanc
10 dit blanc car c est le dernier blanc qui reste
mais pour ça il faut une bonne mémoire car si on oublie les couleur qu'ont dit les autres tu es vraiment:/
a la la maintenant j'ai mal a la tete:rolleyes:
#3 - 21-06-2010 21:15:26
- Nicouj
- Professionnel de Prise2Tete
- Enigmes résolues : 27
- Messages : 330
Escalier e tchapeaux
Le premier compte les chapeaux noirs. Si ce nombre est pair il crie blanc. S'il est impair il crie noir.
Il a un risque sur deux de se tromper. Mais les neuf suivants connaissent la parité du nombres de chapeaux noirs qu'ils portent.
Le deuxième compte aussi les chapeaux noirs qu'il voit. Si la parité de ce qu'il compte change par rapport au premier alors il à un chapeau noir. Sinon il a un chapeau blanc. Il crie la couleur de son chapeau.
Le troisième connait la parité des 9 derniers, calcule celle des 7 derniers qu'il voit et connait la couleur du chapeau du 2eme. Il déduit trivialement la couleur de son chapeau et la crie.
etc...
Le problème se généralise avec un nombre quelconque de couleur de chapeau du moment que les couleurs sont connues a l'avance.
#4 - 22-06-2010 00:02:34
Esalier et chapeaux
En se basant sur le diagramme et en considérant que les 10 hommes ont tous un mode de réflexion cohérent et une certaine mémoire auditive:
On remarque que parmi les 10 hommes, il y a 5 chapeaux noirs et 5 chapeaux blancs, on part du principe que l'homme en haut ne le sait pas mais que son sens de la logique le pousse à penser que c'est le cas, voyant qu'il a en face de lui 5 chapeaux noirs et 4 chapeaux blancs, il dira "blanc", ce sur quoi il aura raison, le deuxième, sachant que la personne derrière lui a un chapeau blanc et voyant que les personnes devant lui ont 4 chapeaux blancs et 4 chapeaux noirs part de la même réflexion logique. Les autres font simplement de même jusqu'à atteindre le dernier qui, sur la base de ce qu'il a entendu déduiras lui-même la couleur de son chapeau !
#5 - 22-06-2010 09:15:32
- MthS-MlndN
- Hors d'u-Sage
- Enigmes résolues : 49
- Messages : 12,414E+3
- Lieu: Rouen
Escalier ett chapeaux
L'idée est sans doute que chacun doit faire savoir au suivant la couleur de son chapeau. Le premier peut dire directement la couleur du chapeau du deuxième, comme ils ont droit à une erreur. Ensuite, ils doivent déterminer d'un signal : chacun dit la couleur de son chapeau, mais avec un petit quelque chose en plus pour dire au suivant s'il a la même couleur de chapeau ou pas. Je suppose qu'un toussotement ou un "euh..." pourrait suffire ?..
Sinon on peut récupérer l'astuce de cette énigme :
http://www.prise2tete.fr/forum/viewtopic.php?id=1365
Le premier dit "noir" s'il compte un nombre pair de chapeaux noirs, "blanc" s'il compte un nombre impair. Les suivants n'ont plus qu'à savoir compter pour déduire la couleur de leurs chapeaux 
Podcasts Modern Zeuhl : http://radio-r2r.fr/?p=298
#6 - 22-06-2010 09:54:33
- croub
- Amateur de Prise2Tete
- Enigmes résolues : 36
- Messages : 2
escalier et chapraux
j'ai une idée, je ne sais pas si ils y ont droit, mais je propose ceci:
le premier répond au hazard, car il n'a aucune indication, et c'est peut etre la seule erreur à laquelle ils ont droit. Mais c'est là que le temps entre en jeu, s'il dit une couleur instantanément, il donne comme info à celui de devant que c'est blanc (par exemple), alors que s'il attend 5 secondes, c'est que celui de devant a un chapeau noir (en suivant la meme logique). Celui de devant devra donc dire la bonne couleur, ou bien instantanémént pour indiquer à celui du dessous qu'il a un chapeau blanc (celui du dessous), ou bien avec un délai de 5 secondes pour lui dire que son chapeau est noir, et ainsi de suite.... On donne l'info au suivant avec le temps quon met à répondre
#7 - 22-06-2010 13:08:49
- McFlambi
- Professionnel de Prise2Tete
- Enigmes résolues : 48
- Messages : 144
Escalier et chapeauxx
attention le dessin illustre, ce n'est pas une indication sur le nombre de chapeaux. Il peut y avoir n'importe quelle série de chapeaux, tous noirs par exemple...
De plus, aucune information à part la couleur criée ne peut être transmise à ceux devant soi...
#8 - 23-06-2010 18:22:52
- Khyros
- Habitué de Prise2Tete
- Enigmes résolues : 23
- Messages : 18
Escalier et chappeaux
Faut que le premier donne un indice qui permettre à tous les autres de connaitre la couleur de leur chapeau...
... Et dans cette situation, sans plus d'informations, et où il n'a le choix qu'entre 2 mots, y'a que la parité du nombre de chapeaux d'une certaine couleur qui fonctionne, à priori.
Solution: S'il voit un nombre pair de chapeaux blancs, il dit blanc. Sinon noir.
Le suivant sait ainsi la couleur de son chapeau en regardant la parité du nombre de chapeaux blancs devant lui, et chacun, en prenant en compte la réponse des précédents, sait ce qu'il porte sur la tête <3
#9 - 23-06-2010 23:08:20
Escalier et chapeauxx
si c ce qu il y a dans l'image alors:
le 1er cris blanc car il voit4blanc et 5noir donc le 2eme saura que son chapeau est noir et ainsi de suite
mais je comprends pas pourquoi y a droit a une erreur
#10 - 24-06-2010 00:28:12
- kosmogol
- Banni
- Enigmes résolues : 49
- Messages : 11,928E+3
escamier et chapeaux
L a part ite me semble correcte !
http://enigmusique.blogspot.com/
#11 - 24-06-2010 04:16:14
esczlier et chapeaux
Le premier dit la couleur de celui qui est devant lui, puisque chaque homme fait de même.
#12 - 24-06-2010 12:47:11
- dhrm77
- L'exilé
- Enigmes résolues : 49
- Messages : 3004
- Lieu: Fanning Island-?-Lac Tele,Mali
Escaliier et chapeaux
Khyros a écrit:Faut que le premier donne un indice qui permettre à tous les autres de connaitre la couleur de leur chapeau...
... Et dans cette situation, sans plus d'informations, et où il n'a le choix qu'entre 2 mots, y'a que la parité du nombre de chapeaux d'une certaine couleur qui fonctionne, à priori.
Solution: S'il voit un nombre pair de chapeaux blancs, il dit blanc. Sinon noir.
Le suivant sait ainsi la couleur de son chapeau en regardant la parité du nombre de chapeaux blancs devant lui, et chacun, en prenant en compte la réponse des précédents, sait ce qu'il porte sur la tête <3
Khyros a raison, c'est bien la facon de faire. Pour violino, c'est simple, le premier n'a aucune indication pour donner la couleur de son chapeau, donc il se sert de son tour pour indiquer a tous les autres la parité de la série de chapeaux, ce qui a une chance sur 2 d'etre faux. Chacun a son tour se sert de la parité, qui alterne a chaque fois que quelqu'un annonce blanc, et en déduit la couleur de son chapeau en fonction de la parité des chapeaux devant lui. Si personne se trompe, il y a au maximum une erreur.
Pour que ca marche, il faut qu'ils se concertent entre eux sur la technique a utiliser, en particulier sur le choix de la couleur a utiliser pour la parité.
Great minds discuss ideas; Average minds discuss events; Small minds discuss people. -Eleanor Roosevelt
#13 - 24-06-2010 13:03:25
- Nicouj
- Professionnel de Prise2Tete
- Enigmes résolues : 27
- Messages : 330
Escalier te chapeaux
Ce qui est magique c'est que même avec n couleurs de chapeau et une seule erreur ils s'en sortent  . Mais faut compter vite et pas être daltonien >< . Mais faut compter vite et pas être daltonien ><
#14 - 24-06-2010 13:21:07
- CIGMA1
- Amateur de Prise2Tete
- Enigmes résolues : 7
- Messages : 3
Escalier et chappeaux
a mon avis tout est question de nombre pair et impair:
le 1er cris la couleur des chapeaux pair si c sa couleur alors les 2 couleurs sont impairs et les autre sauront fair le calcule en s'appuiant sur ce qu'ils avaient entendu et ce qu'ils voient et si c faut alors les 2 couleurs sont pairs et de meme maniere les autres sauront faire le calcule
#15 - 24-06-2010 23:21:46
- shirka
- Amateur de Prise2Tete
- Enigmes résolues : 8
- Messages : 1
Escalier et chapaux
Ben ils ont le droit à une erreur, donc si le premier dit noir et que c'est faux, il dira blanc, donc il aura raison, si le second dit blanc et qu'il a tort, il dira noir car il aussi le droit de se tromper 1 fois, chacune des 10 personnes à le droit à 1 erreur...
#16 - 24-06-2010 23:35:51
- McFlambi
- Professionnel de Prise2Tete
- Enigmes résolues : 48
- Messages : 144
Escalier et chaepaux
ils ont le droit à une erreur en tout ! haha j'adore cette dernière réponse.
bravo à tous ceux qui ont compris la technique de la parité. effectivement comme suggéré plus haut, la même énigme avec autant de couleurs que l'on veut est aussi résoluble avec une seule erreur.
CIGMA1 tu sers à rien. Désolé Modération mais remarque méritée, comme une claque à un enfant. Réponds correctement, avec un bon français, sois poli, relis-toi etc., et je m'abstiendrais de te faire la leçon.
#17 - 24-06-2010 23:40:18
- McFlambi
- Professionnel de Prise2Tete
- Enigmes résolues : 48
- Messages : 144
Escalier et chpeaux
Non mais sérieux, en gras et étoiles les fautes, sans parler de la grammaire, de la syntaxe ou du style... Je t'en foutrais moi des SMS [Désolé Oh Modération].
CIGMA1 a écrit:a mon avis tout est question de nombre pair et impair:
le 1er cris la couleur des chapeaux pair* si c sa couleur alors les 2 couleurs sont impairs et les autre* sauront fair* le calcule en s'appuiant sur ce qu'ils avaient entendu et ce qu'ils voient et si c faut alors les 2 couleurs sont pair*s et de meme maniere les autres sauront faire le calcule
#18 - 25-06-2010 03:50:06
- dhrm77
- L'exilé
- Enigmes résolues : 49
- Messages : 3004
- Lieu: Fanning Island-?-Lac Tele,Mali
escalizr et chapeaux
Nicouj a écrit:Ce qui est magique c'est que même avec n couleurs de chapeau et une seule erreur ils s'en sortent  . Mais faut compter vite et pas être daltonien >< . Mais faut compter vite et pas être daltonien ><
Faux.
En extrapolant le systeme de parite de chaque couleur:
Pour 3, 4 ou 5 couleurs de chapeaux, on a besoin de 2 erreurs.
Par exemple, s'il y a 4 couleurs (bleu, rouge, jaune, vert par exemple), et 100 personnes (X), le premier donne la parite des bleus et des rouges sur les 98 dernieres =X-(N-1) personnes restantes, le 2eme des verts et des jaunes sur ces memes 98 personnes.
Pour donner la parite de 2 couleurs en citant une couleur sur 4, il suffit de definir un tableau avec la parite d'une couleur en horizontal, et la parite de l'autre en vertical. Chaque couleur correspond alors a un cas sur les 4.
A ce moment si tout le monde a suivi, le reste des personnes connait exactement la parité des 4 couleurs.
Avec 6, 7, 8, 9 ou 10 couleurs on a besoin de 3 erreurs en utilisant un tableau à 3 dimensions.
Pour un nombre de couleurs different de 2, 4, 8, 16, etc... c'est un peu plus complexe, mais certainement realisable.
Great minds discuss ideas; Average minds discuss events; Small minds discuss people. -Eleanor Roosevelt
#19 - 25-06-2010 09:45:57
- Nicouj
- Professionnel de Prise2Tete
- Enigmes résolues : 27
- Messages : 330
Escalier et chapaux
sisi ^^
C'est juste que la bonne transposition du problème n'est pas de déterminer la parité de chaque couleur. En effet la parité d'une couleur est une information pauvre alors qu'on a n réponses possibles à chaque fois si il y a n couleurs.
Même en donnant plusieurs parités d'un coup car il faudrait 1 bit par couleur et n bits pour tout coder et une réponse permet de donner log_2(n) bit a chaque coup.
La bonne transposition est de faire la somme des chapeaux (de leur nombre attribué) et de donner le résultat modulo n en criant la couleur associée pour le premier.
Les autres feront la même opération et ajusteront en fonction des réponses précédentes pour trouver leur couleur et la crier.
C'est exactement ce qu'on fait pour le cas 2 couleurs ici et qui va marcher de la même façon. la seule différence est que la seule erreur possible est plus probable avec un nombre élevé de couleur.
#20 - 25-06-2010 10:44:09
- Klimrod
- Elite de Prise2Tete
- Enigmes résolues : 40
- Messages : 4054
- Lieu: hébesphénorotonde triangulaire
Escalier et chapaux
Waow ! Ca, c'est fort ! Chapeau bas ! 
J'ai tant besoin de temps pour buller qu'il n'en reste plus assez pour bosser. Qui vit sans folie n'est pas si sage qu'il croit.
#21 - 25-06-2010 12:42:13
- dhrm77
- L'exilé
- Enigmes résolues : 49
- Messages : 3004
- Lieu: Fanning Island-?-Lac Tele,Mali
Escalier et chapaux
Nicouj, tu pourrais pas donner un exemple de ce que tu explique?
Great minds discuss ideas; Average minds discuss events; Small minds discuss people. -Eleanor Roosevelt
#22 - 25-06-2010 13:00:23
- Klimrod
- Elite de Prise2Tete
- Enigmes résolues : 40
- Messages : 4054
- Lieu: hébesphénorotonde triangulaire
Escalier et hcapeaux
Prenons l'exemple de 4 couleurs : rouge, vert, bleu et jaune.
Conventionnellement, on numérote rouge = 1, vert = 2, bleu = 3 et jaune = 4.
- Le premier personnage compte le nombre de chapeaux rouges qu'il voit devant lui et il multiplie par 1.
- Puis il compte le nombre de chapeaux verts qu'il voit devant lui et il le multiplie par 2.
- Idem avec les chapeaux bleus, qu'il multiplie par 3.
- Il ne fait rien avec les chapeaux jaunes.
- Il additionne ensuite l'ensemble des trois nombres calculés et il prend le modulo 4.
- Il annonce alors haut et fort le modulo 4 trouvé (jaune si ce modulo 4 est égal = 0)
Le personnage suivant fait de même et la différence avec son prédécesseur pemet d'affirmer avec force la couleur de son propre chapeau :
- une différence de 1 = chapeau rouge,
- une différence de 2 = chapeau vert,
- une différence de 3 = chapeau bleu
- pas de différence = chapeau jaune.
C'est facile de généraliser à un nombre quelconque de couleurs et un nombre quelconque de personnages.
La solution est tout simplement géniale ! Chapeau bas !
J'ai tant besoin de temps pour buller qu'il n'en reste plus assez pour bosser. Qui vit sans folie n'est pas si sage qu'il croit.
#23 - 25-06-2010 13:07:24
- Nicouj
- Professionnel de Prise2Tete
- Enigmes résolues : 27
- Messages : 330
Escalier et chapeuax
disons qu'il y a 10 couleurs (on associe les entiers de 0 à 9) et 5 prisonniers pour faire simple.
Les 5 prisonniers sont représentés par la séquence 5 9 2 9 4 par ex.
le premier calcule 9 + 2 + 9 + 4 = 4 modulo 10 et crie le nom de la couleur no 4. (pas de bol c'est pas la sienne mais 1 erreur est tolérée)
le deuxième calcule 2 + 9 + 4 = 5 modulo 10 et déduit sa couleur en faisant la différence entre ce qu'il entend et ce qu'il voit 4 - 5 = 9 modulo 10 il crie 9.
le troisième calcule 9 + 4 = 3 modulo 10 et calcule sa couleur (4 - 9 - 3 = 2 modulo 10 il crie 2
le 4 voit juste un chapeau : 4 il calcule sa couleur : 4 - 9 - 2 - 4 = 9 modulo 10
il crie sa couleur 9.
le dernier calcule sa couleur : 4 - 9 - 2 - 9 = 4 modulo 10
il crie 4.
Un poil plus formel :
le premier calcule et crie c2 + c3 + c4 + ... modulo n
le deuxieme calcule et crie (c2 + c3 + c4 + ... modulo n) - (c3 +c4+ ...) modulo n = c2.
le troisieme calcule et crie (c2 + c3 + c4 + ... modulo n) - c2 - (c4+ ...) modulo n = c3.
etc
#24 - 25-06-2010 14:18:10
- MthS-MlndN
- Hors d'u-Sage
- Enigmes résolues : 49
- Messages : 12,414E+3
- Lieu: Rouen
Escalieer et chapeaux
McFlambi a écrit:CIGMA1 tu sers à rien. (...)
Tu le connais déjà, non ? Un pote à toi ? 
Podcasts Modern Zeuhl : http://radio-r2r.fr/?p=298
#25 - 27-06-2010 13:13:03
- McFlambi
- Professionnel de Prise2Tete
- Enigmes résolues : 48
- Messages : 144
escalier et chapzaux
haha non merci je m'en passerais
Mots clés des moteurs de recherche
|
 |

 Accueil
Accueil
 Forum
Forum






