 |
#1 - 16-11-2012 19:11:51
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
#2 - 16-11-2012 19:31:37
- godisdead
- Expert de Prise2Tete
- Enigmes résolues : 22
- Messages : 747
Gâteeau 56
Moi non plus, je n'y arrive pas. J'attends la réponse avec impatience (si c'est autre chose que "on ne peut pas"  ) )
#3 - 16-11-2012 19:35:31
- titoufred
- Elite de Prise2Tete
- Enigmes résolues : 20
- Messages : 1749
gâyeau 56
Le gâteau doit-il être polygonal ou peut-il être quelconque ?
#4 - 16-11-2012 19:48:20
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
âteau 56
Le gâteau est polygonal comme le suggère le dessin 
Vasimolo
#5 - 16-11-2012 20:00:11
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3839
Gâtea u56
Aux 2 sommets de chaque coté du gâteau, on trace une perpendiculaire à ce coté qui rejoint le carré. L'intervalle sur le carré entre ces 2 perpendiculaires est au minimum aussi long que le coté. Et comme le gâteau est convexe, il y a des zones du carré non comprises dans ces intervalles, ce qui prouve la plus grande longueur du carré.
#6 - 16-11-2012 20:09:56
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
Gââteau 56
Oui Nodgim , c'est une façon de voir les choses , je passe le message au pâtissier 
Vasimolo
#7 - 16-11-2012 20:15:33
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3839
gâtzau 56
Ce n'est pas ta solution ?
#8 - 16-11-2012 20:31:14
- Franky1103
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 3238
- Lieu: Luxembourg
Gâteua 56
On ne peut pas y arriver et c'est la contrainte de convexité qui pose un problème. En le considèrant comme un polygone avec une infinité de côtés de longueur nulle, un cercle sera la figure la plus convexe possible. Puisque pi < 4, le périmètre du meilleur gâteau candidat sera toujours inférieur à celui de la boite.
#9 - 16-11-2012 23:04:13
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
hâteau 56
@Nodgim : ce n'est pas ma solution mais je prends 
@Francky : ce n'est pas si simple , rien ne dit que le gâteau tient dans un disque qui tient dans la boîte .
Vasimolo
#10 - 17-11-2012 00:11:36
- titoufred
- Elite de Prise2Tete
- Enigmes résolues : 20
- Messages : 1749
Gâteeau 56
On ne peut pas réaliser un tel gâteau.
Voici les idées de la démonstration, que je ne formalise pas volontairement :
On considère 4 sommets extrémaux du gâteau H, B, G, D (haut, bas, gauche, droite).
En partant de G pour joindre D, il y a alors deux chemins de sommets possibles, où l'on se déplace toujours de la gauche vers la droite. En effet s'il y avait un retour vers la gauche cela contredirait la convexité.
Idem avec haut/bas.
On peut alors (éventuellement) insérer des nouveaux sommets entre chaque paire de sommets consécutifs, de façon à ce que les bords deviennent tous horizontaux ou verticaux. Entre [latex](x;y)[/latex] et [latex](x';y')[/latex], on insère éventuellement [latex](x;y')[/latex].
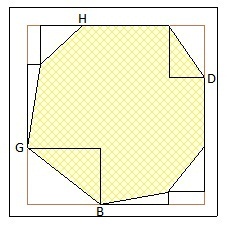
On obtient un nouveau gâteau/polygone dont le périmètre est supérieur ou égal au gâteau/polygone original car le plus court chemin entre 2 points est la ligne droite.
Le périmètre du nouveau gâteau peut alors se calculer facilement :
La somme des côtés horizontaux vaut [latex]2(x_D-x_G)[/latex]
(En partant de G pour joindre D, l'on se déplace toujours de la gauche vers la droite de sommet en sommet.)
De même, la somme des côtés verticaux vaut [latex]2(y_H-y_B)[/latex]
On en conclut que le périmètre du nouveau gâteau et a fortiori du gâteau original est inférieur ou égal au périmètre de la boite.
#11 - 17-11-2012 09:08:35
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
Gâteauu 56
Oui Titoufred , voilà donc une 3ème façon de faire 
Vasimolo
#12 - 17-11-2012 09:14:17
- halloduda
- Professionnel de Prise2Tete
- Enigmes résolues : 24
- Messages : 495
- Lieu: Ardèche
Gâteauu 56
Ce n'est pas possible.
C'est intuitif, mais on peut le démontrer ainsi :
Les bissectrices des angles aux sommets coupent le carré en des points qui délimitent des entités (segments ou paires de segments).
Chacune de ces entités a une longueur supérieure au côté correspondant du polygone.
D'où par addition le résultat :
Le polygone a un périmètre supérieur à celui de la boîte carrée.
#13 - 17-11-2012 09:22:03
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
gâteay 56
Oui Halloduda ! Encore une nouvelle façon de procéder .
Vasimolo
#14 - 17-11-2012 09:33:12
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 6,194E+3
Gâteau 556
Le gâteau étant convexe, si on si on prend un triangle formé par 3 sommets consécutifs, en augmentant sa hauteur, on augmente son périmètre. On le prolonge donc jusqu'au bord de le boîte obtenant ainsi un gâteau de périmètre plus grand que le gâteau initial. (Cela marche même sans avoir un gâteau octogonal au départ, certains sommets consécutifs seront juste projetés sur le même côté de la boîte)
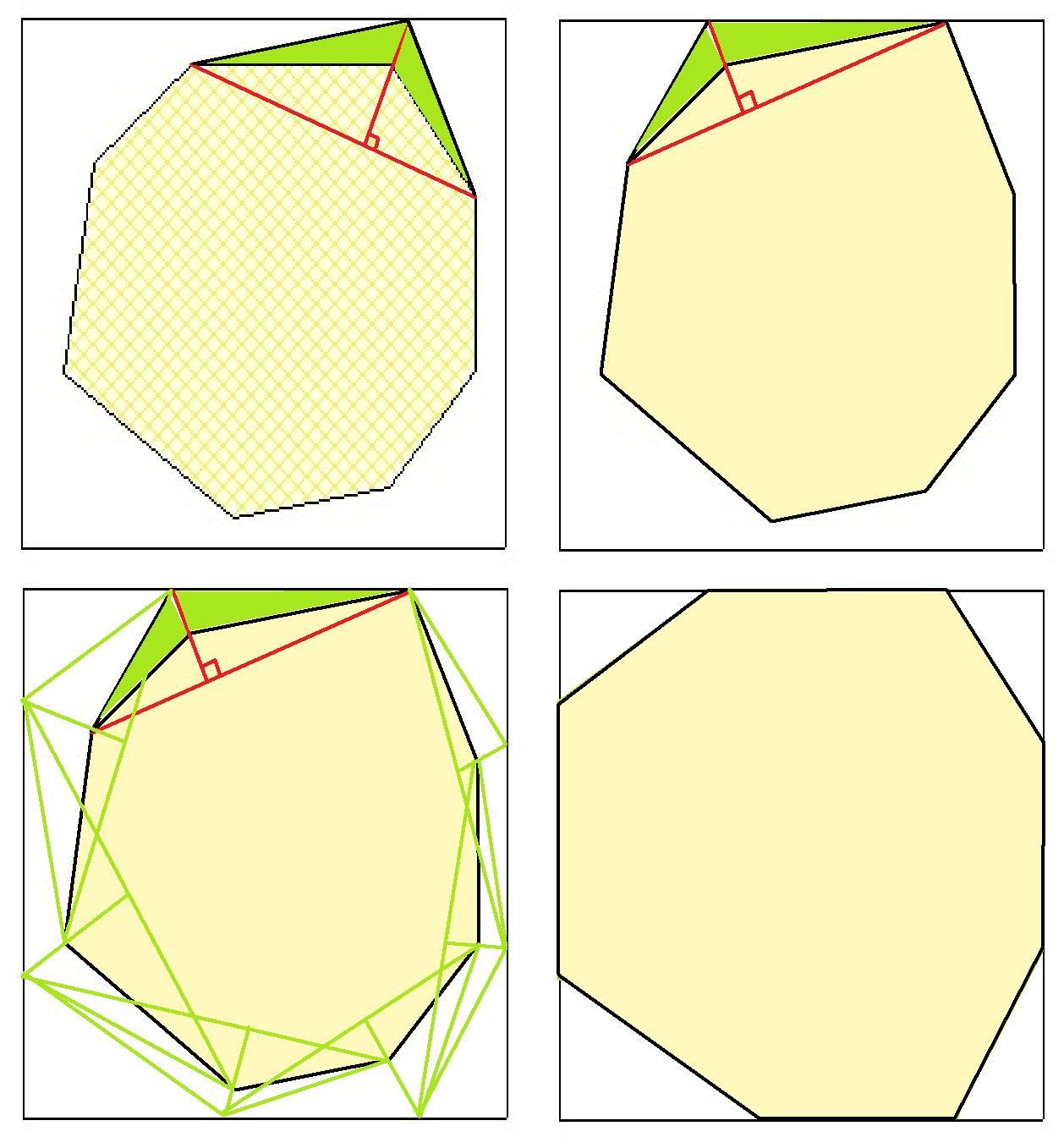
De fil en aiguille, on obtient un octogone inscrit dans la boîte, dont le périmètre, plus grand que celui du gâteau est clairement plus petit que celui de la boîte.
Il est donc impossible d'y arriver.
#15 - 17-11-2012 12:22:55
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
gâteai 56
Et un de plus , bravo Gwen !!!
Vasimolo
#16 - 17-11-2012 13:13:25
- Promath-
- Elite de Prise2Tete
- Enigmes résolues : 18
- Messages : 1416
- Lieu: Au fond de l'univers
Gâteau 556
Peut-on "plier" le gâteau?
Un promath- actif dans un forum actif
#17 - 17-11-2012 14:55:04
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 6,194E+3
gâyeau 56
Juste un essai mais je ne suis pas sûr de moi.
(On n'agrandit plus la forme, on réduit le carré...) pour la même conclusion :
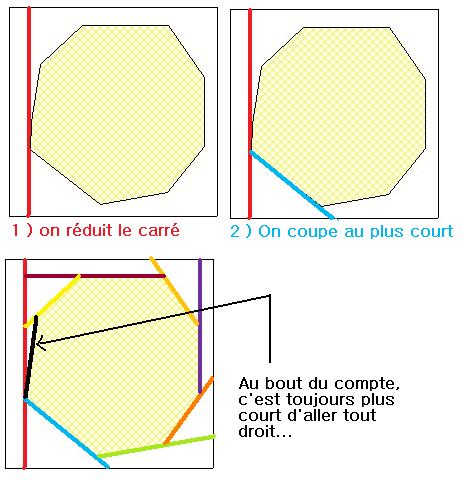
#18 - 17-11-2012 15:50:41
- Jackv
- Elite de Prise2Tete
- Enigmes résolues : 34
- Messages : 3616
- Lieu: 94110
âteau 56
Je commence par supposer que la boîte est rectangulaire (peut-être faudrait-il le présiser au départ ?  ). ).
La boîte de périmètre le plus petit vient toucher le polygone sur un segment ou un point sur chacun des ses cotés.
Considérons un angle A de ce rectangle et la portion de polygone P1-Pn qui vient toucher les cotés adjacents à A en P1 et Pn.
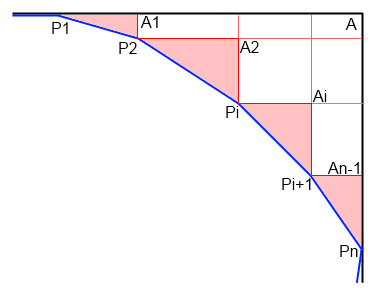
On trace de chaque point Pi les segments parallèles à A-P1 et A-Pn, segments dont les intersections sont les point A1, ... Ai, ... An-1.
On détermine ainsi une ligne polygonale en escalier "P1, A1, ... Pi, Ai, Pi+1, ... An-1, Pn" dont la longueur est égale à P1-A + A-Pn.
Dans chaque triangle rectangle Pi, Ai, Pi+1 l’hypoténuse est inférieure à la somme des cotés de l'angle droit.
La longueur de la suite de segments "P1, ... Pi, ... Pn" est donc inférieure à celle de la suite "P1, A1 ... Pi, Ai, Pi+1, ... An-1, Pn", donc de la somme P1-A + A-Pn.
On peut recommencer ce processus pour chaque sommet du rectangle.
Est-il besoin de rentrer plus dans le détail ?
Remarque 1 : La démonstration reste valable pour une boîte non rectangulaire, que ce soit un quadrilatère ou un polygone à n cotés (n <= nb de cotés du polygone) dont chaque coté vient touché le polygone initial en un point ou un segment.
Il suffit de remplacer alors "triangle rectangle" par "triangle quelconque", et hypoténuse par un coté dont la longueur reste inférieure à la somme des 2 autres  . .
Remarque 2 : En multipliant le nombre de coté de ton polygone, on arrive à une courbe convexe, et on démontre ainsi que la longueur de cette courbe est comprise entre la longueur de tout polygone inscrit dans cette courbe et celle de tout polygone circonscrit à cette courbe  . .
#19 - 17-11-2012 17:27:19
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
gâteai 56
Une nouvelle démonstration de Gwen et une de Jack qui fait remarquer que le résultat reste valable quelle que soit la forme polygonale de la boîte .
En fait le résultat est valable pour toute boîte avec un gâteau convexe .
Vasimolo
PS : @Promath : on ne "plie" pas le gâteau 
#20 - 17-11-2012 18:30:03
- titoufred
- Elite de Prise2Tete
- Enigmes résolues : 20
- Messages : 1749
âGteau 56
Pour une boite rectangulaire (définissant des notions de gauche/droite et haut/bas),
le résultat reste valable pour des gâteaux non convexes du moment que pour aller de G à D (resp. de B à H), on se déplace toujours vers la droite (resp. le haut).
Par exemple, pour une étoile à 4 branches (placée dans la boite comme ci-dessous) :

#21 - 17-11-2012 19:50:16
- gabrielduflot
- Expert de Prise2Tete
- Enigmes résolues : 34
- Messages : 614
Gâtea u56
Le gateau convexe que l'on peut faire est celui du contour de la boîte carré car s'il on prend deux points sur le bord de deux cotés consécutifs l'inégalité triangulaire dans un triangle nous prouve que c < a+b danc le périmètre du polygone sera inférieur a celui de la boîte qui est carré
#22 - 18-11-2012 12:12:53
- MthS-MlndN
- Hors d'u-Sage
- Enigmes résolues : 49
- Messages : 12,414E+3
- Lieu: Rouen
Gâetau 56
Je dirais simplement qu'on peut obtenir la forme du gâteau en partant de la forme de la boîte et en appliquant des découpes successives, chaque coupe consistant à tracer une ligne droite dans un polygone.
Ce polygone est convexe à n'importe quel moment par construction, et chaque découpe va raccourcir le périmètre du polygone, puisque la zone supprimée sera également un polygone convexe dont on gardera un seul côté en supprimant tous les autres.
Donc notre pâtissier semble mal barré ^^
Podcasts Modern Zeuhl : http://radio-r2r.fr/?p=298
#23 - 18-11-2012 12:19:39
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
Gââteau 56
Bien vu Mathias 
C'est assez impressionnant de voir le nombre de façons d'aborder le problème selon ses goûts ou ses habitudes .
Bon courage à ceux qui cherchent encore .
Vasimolo
#24 - 18-11-2012 20:23:27
- golgot59
- Elite de Prise2Tete
- Enigmes résolues : 48
- Messages : 1494
- Lieu: Coutiches
Gâtea u56
Je trouve que c'est impossible, en gros sur le principe que le plus court chemin d'un point à un autre est la ligne droite...
Mais je ne parviens pas à faire une démo rigoureuse. 
#25 - 18-11-2012 23:15:56
- looozer
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 697
- Lieu: Belgique
Gâtteau 56
Réponse un peu facile, mais si on peut choisir la hauteur de la boîte et celle du gâteau (ce que l'énoncé n'interdit pas), il suffit d'un truc dans ce genre :
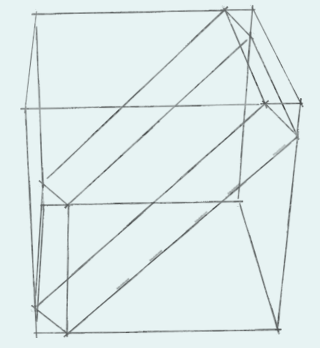
On disait que le gâteau était bien rigide ;-)
Mots clés des moteurs de recherche
|
 |

 Accueil
Accueil
 Forum
Forum













