Enigme Gâteau 127 @ Prise2Tete

Vasimolo · #1

Bonsoir à tous .

Une version corrigée du gâteau ( Merci à Ebichu )

Mon pâtissier expose un curieux gâteau sur la devanture de son magasin :

Le gâteau pèse moins de 1,5 kg et la masse de chaque part est un nombre entier de grammes ( non nul ).

Sous le gâteau il a posé une étiquette :

"Tu ne connais pas la taille des parts mais tu pourrais la trouver si je te donnais la masse du gâteau . Si le gâteau pesait un gramme de plus ou un gramme de moins tu t'en sortirais aussi bien" .

Quelle est donc la taille de chacune des parts ???

Amusez-vous bien

Vasimolo

PS : la case réponse valide les masses des parts en ordre croissant et en grammes , deux parts sont séparées par une virgule .

Indice 1 : Spoiler : [Afficher le message]

Indice 2 :Spoiler : [Afficher le message]

Vasimolo · #2

A la demande express de Dan , j'ajoute un peu de temps . Je me laisse bien sûr le droit de lever le masque ( ou d'allonger la durée ) à tout moment

Vasimolo

PS : je n'aime pas les longues discussions en aveugle , il y a peu d'échanges et beaucoup de redites qui n'encouragent personne à revenir sur le problème lorsque les réponses deviennent visibles .

D'un autre côté ce gâteau n'est pas un cadeau , il mérite un peu de temps .

unecoudée · #3

bonsoir.

j'ai un mauvais gateau ( parce que l'un de ses voisins est premier et l'autre est un carré de premier ( 37² ) . pas de pot .

je désigne par t l'aire du gateau . t = 1368
a la part jaune du centre
b la part bleu ciel
c la part rouge
d la part verte

la découpe de ce gâteau donne :
t = 1368 , e = 456 , a = 119 , b = 357 , c = 147 , d = 289
en effet par construction : a.b = c.d ; a.t = e.b

deux autres gâteaux donnent :
t = 1440 , e = 360 , a = 120 , b = 480 , c = d = 240
mais son voisin 1439 est aussi premier
par homothétie 1320 = 11/12 x 1440
t = 1320 , e = 330 , a = 110 , b = 440 , c = d = 220

peut-être qu'il existe un système de formules pour déterminer 3 nombres voisins répondant aux critères.

Vasimolo · #4

Bonsoir Unecoudée

Le problème avec tes gâteaux ( en dehors du fait qu'ils n'ont pas leurs deux voisins satisfaisants ) est qu'ils autorisent de nombreux partages différents : on ne peut pas deviner la taille de chacune des parts .

Sinon , je n'ai pas trouvé de solution à la main , j'ai fait tourner un petit programme en m'inspirant des égalités que tu as citées .

Bon courage !

Vasimolo

dhrm77 · #5

petit programme, petit programme... Il faut le dire vite... mon petit programme fait deja 300 lignes et est encore assez loin de trouver la solution...
Peut-etre que je m'y prend mal en essayant de composer des triangles de plus en plus gros en partant de petits triangles de base... C'est pas simple d'éliminer les cas ou les triangles ne s'alignent pas correctement.
Sinon des triangles formés de petits triangles de valeur entiere, ca ne manque pas. Pas exemple, un triangle de 1680 grammes peut etre composé de pas moins de 314 petits triangles, mais de trouver par programme s'il existe une configuration qui corresponde a ton image, c'est pas simple...

Vasimolo · #6

@Dan ,

il doit te manquer des relations entre les différentes parts , le programme est relativement simple quand on sait programmer ( ce qui n'est pas mon cas )

Vasimolo

Vasimolo · #7

J'ai ajouté une case réponse pour les timides qui n'osent pas se lancer

Vasimolo

gwen27 · #8

J'ai un peu cherché... et pas trouvé.

Je trouve juste qu'il n'y en a pas: tout comme pour 2000 , il y avait une bonne cinquantaine de solutions différentes, là, soit il n'y en a aucune, soit on tombe sur plusieurs en prenant 1 nombre sur 3 de 0 à 1500.

Vasimolo · #9

Il y a bien une solution Gwen et elle est unique

Si le gâteau faisait moins de 2 kg comme je l'avais proposé initialement il y aurait 4 possibilités , ce qui dégrade un peu l'énigme .

Je précise que je n'ai pas trouvé la solution "à la main " .

Vasimolo

Ebichu · #10

4 possibilités tu es sûr ? Je n'en compte que 2.

Vasimolo · #11

En effet Ebichu , 2 possibilités pour un gâteau inférieur à 2 kg ( je me suis un peu mélangé dans mes données ) .

Vasimolo

Franky1103 · #12

Cette énigme m'intrigue car je ne sais pas par quel bout la prendre.

Comme la surface d'un triangle est le produit de sa hauteur par sa demi-base et que dans un triangle pythagoricien un des deux côtés de l'angle droit est forcément pair, je me dit qu'une condition suffisante (mais pas forcément nécessaire) est que la hauteur et la demi-base soient entières.

Comme ceci concerne, les triangles "bleu clair", "bleu clair + vert" et "bleu clair + rouge", j'en déduit (peut-être un peu vite) que les abscisses et les ordonnées (dans un repère qui va bien) de tous les points d'intersection sont entiers.

Après, j'ai fait plein de calculs (non reproduits ici car inutiles), mais sans succès.
Affaire à suivre ...

Vasimolo · #13

Tu n'es pas sur la même piste que moi Franky mais pourquoi pas ? Il me semble toutefois qu'il te manque une petite relation

Vasimolo

PS : j'ai ajouté un premier indice et j'en fournirai un deuxième si l'envol est laborieux .

enigmatus · #14

Bonjour,
Grâce à ton second indice, j'ai une réponse qui valide la case du même nom.

Code:

S=1245
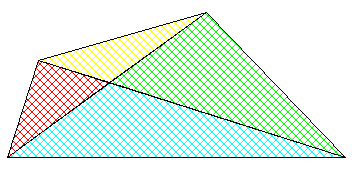
        bleu=249 jaune= 83 rouge=415 vert= 83 cyan=415
        bleu=249 jaune= 83 rouge= 83 vert=415 cyan=415
S=1246
        bleu= 63 jaune= 18 rouge=801 vert=  8 cyan=356
S=1247
        bleu=435 jaune=105 rouge=301 vert=105 cyan=301

Je me suis limité à : côté_gauche_du_grand_triangle <= côté_droit.
On obtient 2 solutions pour S=1245, mais une fois triées, les masses des parts sont identiques.

Vasimolo · #15

C'est ça Enigmatus , bravo !!!

A mon avis , le plus difficile dans le problème est de compter le nombre de gâteaux possibles pour une masse donnée sans compter les gâteaux impossibles ou les doublons avec échange de parts ( d'ailleurs je ne suis pas sûr d'avoir le compte exact pour chaque masse totale ) .

Si on note :

a=bleu
b=jaune
c=indigo
d=rouge
e=vert

Pour c , d et e entiers donnés , a et b sont donnés par les relations :

bc=de
ac=bt
a+b+c+d+e=t ( avec t=a+b+c+d+e ).

Il faut bien sûr vérifier que a et b sont bien entiers .

Pour la recherche des solutions à partir d'une masse donnée il me semble plus simple de partir b puis a puis d , on calcule alors c et d et on vérifie que tout marche . On peut facilement limiter l'étude par symétrie . Il faut quand même vérifier que l'ensemble des solutions fournies ne se ramène pas à une permutation des parts ( personnellement j'ai vérifié à la main ) .

Vasimolo

enigmatus · #16

Au cas où ça intéresse quelqu'un, je joins mon script python :

Code:

'''
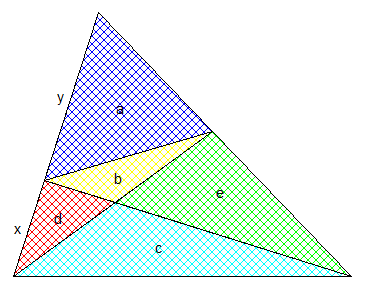
               A
               s1
          b          c
               s2
            s3    s4
               s5
B                                C
'''

resul={}
se_suivent=[0]
def resol(S):
   global se_suivent
   n=0
   resu=set()
   for AB in range(2,S+1):
      if S%AB: continue
      AC=S//AB
      if AC<AB: continue
      for Ab in range(1,AB):
         for Ac in range(1,AC):
            s1=Ab*Ac
            s123=AB*Ac
            if s123<3: continue
            s23=s123-s1
            s124=Ab*AC
            if s124<3: continue
            s24=s124-s1
            s35=S-s124
            s45=S-s123
            for s2 in range(1,min(s23,s24)):
               s4=s24-s2
               s5=s45-s4
               s3=s35-s5
               if s2*s5==s3*s4:
                  n+=1
                  s12345t=tuple(sorted((s1,s2,s3,s4,s5)))
                  if S not in resul: resul[S]=set()
                  resul[S].add((S,AB,AC,Ab,Ac,s1,s2,s3,s4,s5))
                  resu.add(s12345t)
   if len(resu)==1:
      if S==se_suivent[-1]-1: se_suivent.append(S)
      else: se_suivent=[S]
      if len(se_suivent)==3:
         for s in (S,S+1,S+2):
            print("S=%4s"%s)
            for k in resul[s]:
               print("AB=%3s AC=%3s Ab=%3s Ac=%3s bleu=%3s jaune=%3s rouge=%3s vert=%3s cyan=%3s"%k[1:])
         exit()
   return n
S=1500
while True:
   resol(S)
   S-=1
   if S<5: break

qui donne ce résultat :

Code:

S=1245
AB=  3 AC=415 Ab=  1 Ac=249 bleu=249 jaune= 83 rouge=415 vert= 83 cyan=415
AB=  5 AC=249 Ab=  3 Ac= 83 bleu=249 jaune= 83 rouge= 83 vert=415 cyan=415
S=1246
AB= 14 AC= 89 Ab=  1 Ac= 63 bleu= 63 jaune= 18 rouge=801 vert=  8 cyan=356
S=1247
AB= 29 AC= 43 Ab= 15 Ac= 29 bleu=435 jaune=105 rouge=301 vert=105 cyan=301

Franky1103 · #17

bc=de
ac=bt

Par "construction", cela semble évident pour tout le monde, mais pas pour moi. Pourrait-on, svp, avoir une explication (ou encore mieux une démonstration) ?

Vasimolo · #18

Pour bc=de , il suffit d'appliquer la loi des sinus dans chacune des parts b,c,d,e .

Pour la deuxième relation : le triangle b+d de base x et le triangle a de base y ont la même hauteur donc x/y=(b+d)/a de même pour les triangles c+d et a+b+e donc x/y= (c+d)/(a+b+e) . Il n'y a plus qu'à effectuer les produits en croix et remplacer de par bc .

Vasimolo

Franky1103 · #19

C'est clair maintenant: merci.

Forum dédié aux énigmes et à toutes formes de jeux de logique.	Déconnexion
Tu n'es pas identifié sur Prise2tete : s'identifier. Accueil Forum	[+]

#1 - 23-09-2016 23:14:17

gâtezu 127

#0 Pub

#2 - 25-09-2016 18:51:36

Gâtteau 127

#3 - 25-09-2016 20:08:36

Gâteau 27

#4 - 26-09-2016 16:42:15

Gâteu 127

#5 - 26-09-2016 20:17:13

âteau 127

#6 - 26-09-2016 20:43:42

gâteay 127

#7 - 27-09-2016 17:16:57

Gâteauu 127

#8 - 28-09-2016 20:37:37

Gâteu 127

#9 - 29-09-2016 10:03:12

âGteau 127

#10 - 29-09-2016 13:27:02

Gteau 127

#11 - 29-09-2016 15:40:42

Gâteeau 127

#12 - 30-09-2016 10:38:02

gâteay 127

#13 - 30-09-2016 18:02:51

Gâetau 127

#14 - 05-10-2016 15:00:26

hâteau 127

Code:

#15 - 05-10-2016 18:05:08

Gtâeau 127

#16 - 05-10-2016 21:48:18

GGâteau 127

Code:

Code:

#17 - 06-10-2016 05:40:17

Gâteaau 127

#18 - 06-10-2016 17:46:13

âteau 127

#19 - 08-10-2016 20:07:16

Gâteau 172

Réponse rapide

Sujets similaires

Pied de page des forums