Forum dédié aux énigmes et à toutes formes de jeux de logique. | Déconnexion |
|
Tu n'es pas identifié sur Prise2tete : s'identifier.  Accueil Accueil
 Forum Forum
|
 |
#1 - 08-04-2018 11:42:22
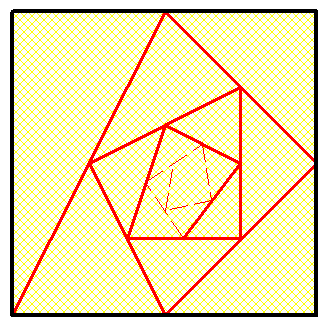
Gâteau 1550Un petit gâteau léger pour nous reposer des précédents
#0 Pub#2 - 08-04-2018 12:11:12#3 - 08-04-2018 16:57:52#4 - 08-04-2018 17:02:48#5 - 08-04-2018 17:16:41#6 - 08-04-2018 19:44:10
Gâteau 105Bonjour Vasimolo et merci pour ce problème. #7 - 08-04-2018 23:23:36#8 - 09-04-2018 17:19:06#9 - 09-04-2018 19:56:47#10 - 09-04-2018 21:38:55
Gâteau 1500Je trouve le point de coordonnées 16 cm et 12 cm. #11 - 10-04-2018 07:32:46
gâyeau 150On traite séparément les x des y. #12 - 10-04-2018 12:58:19#13 - 10-04-2018 17:35:28#14 - 10-04-2018 20:40:19#15 - 11-04-2018 17:45:19
Gâtteau 150Il est amusant de voir que pour 4 points consécutifs la somme des abscisses [latex]x_n+2x_{n+1}+2x_{n+2}+2x_{n+3}[/latex] est constante et vaut 7 fois l'abscisse de la limite . De même pour les ordonnées et on obtient le point d'arrivée : (16;12) . Réponse rapideSujets similaires
|
 | |||||||||||||||||||||||||||||||||
| Prise2Tete Forum Statistiques Liste des membres Hall of Fame Contact | |||||||||||||||||||||||||||||||||||
Un jeu où seules la réflexion, la logique et la déduction permettent de trouver la solution.