Il y a un nombre dont la somme fait 1, deux dont la somme fait 2, quatre dont la somme fait 3. En laissant tomber le 0 (qui fausserait selon toi). Soit il y a six nombres dont la somme vaut trois, soit il y en a 8. Quand j'aurai mieux pigé la logique je le saurais sans doute. Affaire à suivre.

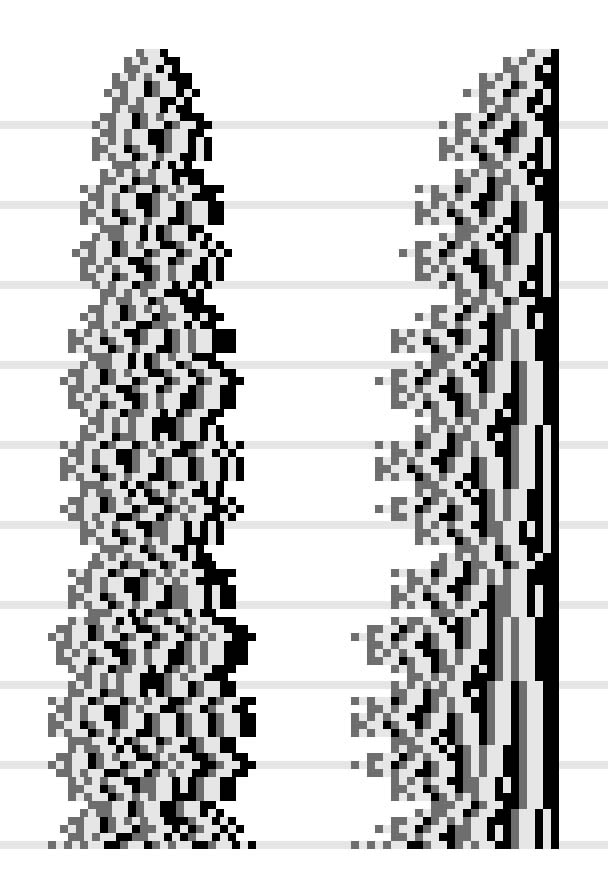
En utilisant cette écriture et "en poussant la logique à l'infini", j'arrive à représenter graphiquement une certaine complexité des entiers.
Sur cette image, de haut en bas, sont représentés les entiers de 1 à 100, un par ligne. Les lignes horizontales en clair représentent les dizaines. 
J'espère que ça vous donnera envie de chercher un peu.

Je viens de remplacer l'image du dessus. Il faut au moins trois couleurs pour représenter de façon unique un entier.

Sinon, je viens de rajouter un très gros indice dans le sujet.

Pour l'instant, SuperCab est le seul a avoir trouvé.

Suite à l'excellente intervention de Rivas, qui m'a donné une très belle interprétation (qui n'était pas la mienne),  je me suis dit, qu'elle pourrait faire un excellent indice (un méga, du coup!).
Voilà chose faite, vous trouverez un dernier indice dans le sujet.
J'espère ne pas gâcher l'éventuel plaisir que vous auriez pu avoir en résolvant cette énigme seul, mais si le fait d'y parvenir, peut vous en donner un peu... je serais bien content.

Voici mon interprétation du code.
Je prends un entier n. Il peut se mettre sous la forme:
n=n0=2n1 si il est pair
n=n0=2n1+1 si il est impair
De la même façon, n1 peut se décomposer en:
n1=2n2 si il est pair
n1=2n2+1 si il est impair
Et ainsi de suite, jusqu'à ce que j'obtienne ni=1.
Si je mémorise le cheminement qui m'y a conduit, j'aurais décrit l'entier initial de façon unique.
Je compte alors les fois de suite où j'obtiens des nombres pairs ou impairs, et je les range entre crochets. Par convention, je choisis de décrire le cheminement par autant "d'opérations pairs que d'impairs" (C1). Autrement dit, le codage de n se fera toujours avec un nombre pair d'entiers. Par convention, le premier nombre de la série traduit des opération impaires" (C2), le second, des opérations pairs, des opérations impaires pour le troisième  etc...
Autant prendre des exemples, ça sera sûrement plus clair:

5=2*2+1, puis 2=2*1
On commence donc par une opération impaire, suivie d'une opération paire.
=> 5 = [1,1]

6=2*3, puis 3=2*1+1
Je commence donc par zéro opération impair (voir C2) puis une paire, une impaire, et zéro pair (voir C1).
=> 6 = [0,1,1,0]

Finalement, les entiers de 11 à 20 se codent ainsi:
11 = [2,1]
12 = [0,2,1,0]
13 = [1,1,1,0]
14 = [0,1,2,0]
15 = [3,0]
16 = [0,4]
17 = [1,3]
18 = [0,1,1,2]
19 = [2,2]
20 = [0,2,1,1]

Bravo à Supercab et Rivas qui ont compris cette logique. Je vous invite à lire la réponse de rivas qui donne une belle interprétation et fait un rapprochement intéressant avec l'écriture binaire.

Bon, ce que j'ai expliqué plus haut, c'est la version "simple" (j'avais dit que des notions de base étaient suffisantes...), qui à sûrement l'avantage de pouvoir être comprise par un plus grand nombre mais qui est à mon sens, pas très rigoureuse. En particulier, l'écriture de 1 est ambigüe avec ces seules explications...

J'ai donc introduit deux fonctions f et g telles que:
[TeX]f(x)=2x+1[/latex] et [latex]g(x)=2x[/TeX]
J'utilise la notation suivante pour les composées:
[TeX]f^{m}(x)=(\underbrace{f\circ f\circ ...\circ f}_{m\times})(x)[/TeX]
Alors, je propose que:
[TeX]\forall n \in \mathbb{N}^*, \exists !p\in \mathbb{N}^*, \exists !(m_1, m_2,...,m_{2p})\in\mathbb{N}\times\mathbb{N}^{*2(p-1)}\times\mathbb{N} \backslash n=(f^{m_1}\circ g^{m_2}\circ ...\circ g^{m_{2p}})(1)[/TeX]
Vous l'avez donc compris, le vecteur [latex](m_1, m_2,...,m_{2p})[/latex] constitue le codage (et je ne sais pas pourquoi j'ai introduit des crochets! )
Puisque toute fonction composée zéro fois, est la fonction identité, on a bien [latex](f^0\circ g^0)(1)=1[/latex], ce qui explique le codage de 1.

Deux mots sur l'image du dessus.
De la même façon, on peut coder ou décomposer les entiers [latex]m_i[/latex] jusqu'à l'obtention de 0 uniquement. Un exemple...
2 = [0,1] = [0,[0,0]]
4 = [0,2] = [0,[0,[0,0]]]

En remplaçant les "[", "0" et "]" par trois couleurs différentes, on obtient alors la représentation graphique que j'ai donné ci-dessus (on peut se passer de représenter le "," car le "0" n'est qu'un chiffre...).
Je trouve ça assez intéressant de "mettre à jour" un certain coté chaotique dans la suite des entiers, tout comme peut l'avoir celle des nombres premiers. Il semble y avoir tout de même un arrangement semi-périodique...

Voila, j'espère ne pas avoir raconté trop de bêtises.
Merci à ceux qui ont participé et cherché.

PS: ah oui, j'oubliais, et pour répondre à Rivas.
Ce qui m'a amené à cette écriture n'est pas la suite Conway, mais la suite de Syracuse. En essayant d'exprimer les termes de cette suite (même pas peur! ), c'est venu "assez naturellement"... Peut-être que je proposerai ce que j'ai fait sous forme d'une énigme, c'est assez amusant, d'ailleurs le sujet de ma nouvelle énigme est issu également d'une réflexion à propos de cette même fameuse suite.

Un combiné du binaire et de la suite de Conway, j'ai traité les deux séparément ! è_é