 |
#1 - 26-03-2011 19:53:00
- looozer
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 697
- Lieu: Belgique
Éqquilibre précaire
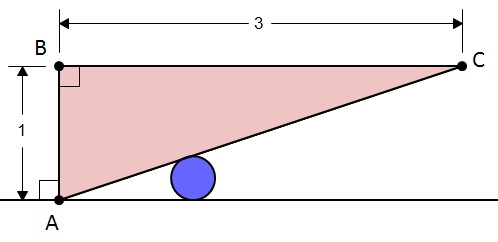
Un sculpteur d'avant-garde a placé dans un parc son oeuvre intitulée "La Flèche de l'Infini".
La pièce principale est appuyée contre un cylindre fixe dont la taille a été réduite au maximum sans malgré tout permettre le basculement lorsque l'oeuvre repose sur un plan horizontal.
1. Que vaut le rayon de ce cylindre?
2. L'artiste (décidément cinglé) planche sur une seconde version de même hauteur pour laquelle il compte étirer le côté horizontal de 3m jusqu'à... l'infini! Quel rayon doit-il prévoir pour le cylindre support?
Remarques : le cylindre est fixé sur le sol, il ne peut donc ni glisser ni rouler.
La pièce principale est simplement posée sur le point A et le point de tangence avec le cylindre.
#2 - 27-03-2011 05:18:15
- mitsuidewi
- Professionnel de Prise2Tete
- Enigmes résolues : 49
- Messages : 250
- Lieu: dans une chambre universitaire
Équiilibre précaire
cas où BC=3:
[TeX]\frac{y}{3}=x \; et \; \frac{xy}{2}=\frac{3}{4}[/TeX][TeX]\Rightarrow \, x=\frac{1}{\sqrt{2}}[/TeX]
D'où [latex]R=\frac{2-\sqrt{2}}{4}[/latex]
Pour le cas AB=z = infini, on remarque que les calculs ne dépendent pas de z, d'où le résultat constant [latex]R=\frac{2-\sqrt{2}}{4}[/latex], simplement le cylindre sera déplacé vers l'infini vers la droite.
Je modifie mon post à ta demande, voici ma méthode :

#3 - 27-03-2011 14:20:51
- halloduda
- Professionnel de Prise2Tete
- Enigmes résolues : 24
- Messages : 495
- Lieu: Ardèche
Équilibre précare
1. Le centre du cercle est :
- sur la bissectrice de l'angle xAC
- sur la perpendiculaire à AC passant par le point de contact (1, 1/3)
(à l'aplomb du centre de gravité du triangle)
Le rayon est donc [latex](\frac13) AC \,\tan\frac {\arctan\frac1 3 }2[/latex]
soit [latex]\frac {10} 3-\sqr{10} \approx [/latex] 0.17105567
2. Quand le triangle s'étire à l'infini, le rayon tend vers [latex]\frac 1 6 \approx[/latex] 0.166667
#4 - 28-03-2011 11:36:33
- Jackv
- Elite de Prise2Tete
- Enigmes résolues : 34
- Messages : 3614
- Lieu: 94110
Équilibre pprécaire
Ah que voilà un p'tit problème de mécanique qu'il est intéressant !
Que le cylindre ne puisse pas bouger, c'est une chose qu'il fallait effectivement préciser.
Il suffit d'ailleurs pour cela que le coefficient d'adhérence entre le cylindre et chacune des deux surfaces en contact soit supérieur à [latex]tg(1/2*arctg(1/3))[/latex], soit [latex]f > 0.16228[/latex] (ce qui est tout à fait plausible) pour éviter de mettre de la colle.
Mais il faut aussi que le point A ne glisse pas sur le sol !
Pour faire confiance au frottement dans le cas où l'on place le cylindre au plus près du centre de gravité de la pièce principale, il faudrait que le coefficient d'adhérence au point A soit supérieur à 3, ce qui est rigoureusement impossible (Les meilleurs dragsters, avec une gomme spéciale dont une bonne partie reste sur le bitume, dépasse à peine un coefficient de 1 ce qui leur permet d'obtenir une accélération légèrement supérieure à g).
Ceci étant posé, considérons d'abord l'équilibre du cylindre : il est soumis seulement à 2 forces, donc celle-ci sont colinéaires et passent par les points de contact.
Considérons maintenant l'équilibre de la pièce principale : elle est soumise à 3 forces :
- son poids P, vertical et passant par le centre de gravité G ; ce point est situé à une abscisse de 1 par rapport au point A.
- l'action du cylindre FD dont on connaît maintenant la direction et le point d'application.
- l'action du sol en A dont on ne connaît pas à priori la direction.
Dans le cas général l'équilibre de la pièce principale est représenté sur la figure 1 ci-dessous (dans le cas d'un coefficient d'adhérence en A de 0.4, ce qui est déjà beaucoup).
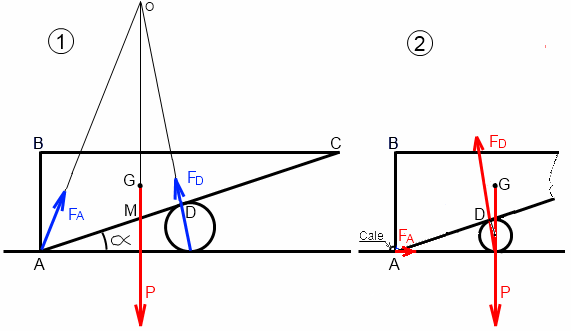
Si on veut utiliser un cylindre plus petit, le mieux serait de fixer une petite cale sur le sol en A pour empêcher ce glissement.
A partir de là, je modifie mon calcul et la figure 2.
Si la pièce est bloquée en A, on peut faire tendre le point de contact D vers le point M, intersection de le centre du cylindre vers la verticale en G et de AB passant par le point G ; le point O tend aussi vers M vers le plan horizontal et l'effort FA prend alors la direction AC horizontale (figure 2).
On a AD = 1/cos A AD = 1, et r = AD * tg (A/2) avec A = arctg (1/3)
d'où : r = 0.17106 0.16228.
Si on réalise une affinité d'axe AB et de rapport ausi grand que l'on veut, on conserve la distance AB, AC tend vers l'horizontale, FD vers la verticale et FA tend vers 0.
Le rayon du cercle tend alors vers 1.66666...
#5 - 28-03-2011 15:40:32
- rivas
- Elite de Prise2Tete
- Enigmes résolues : 48
- Messages : 1106
- Lieu: Jacou
Équilibe précaire
Je me lance... Un peu de géométrie de temps en temps, ça ne peut pas faire de mal (quoique  ) )
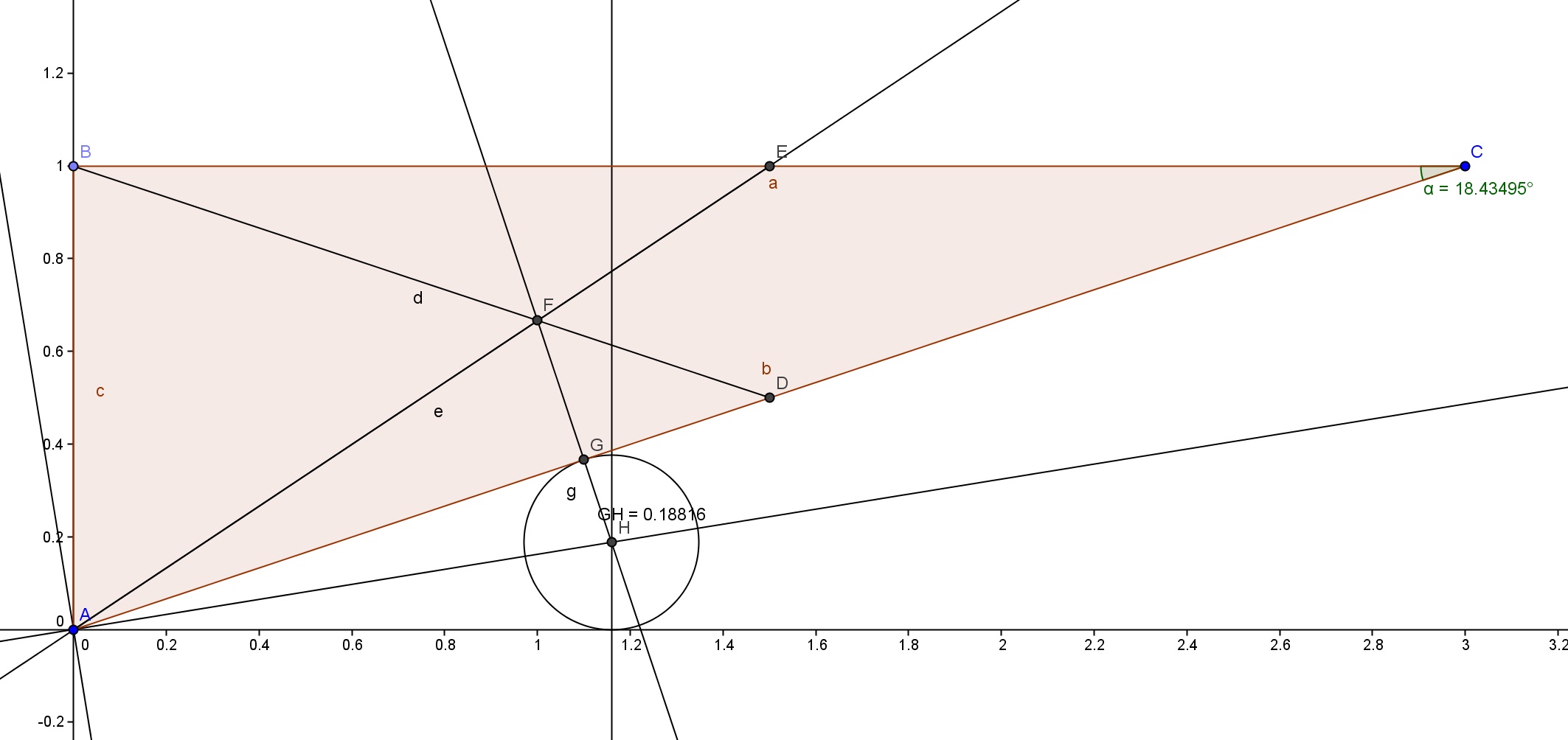
On peut regarder la figure avec l'hypothénuse horizontale. On voit alors beaucoup mieux que l'équilibre est atteint si le centre de gravité est au-dessus du point de contact. On revient dans notre repère. Si on déplace le cylindre vers la gauche en en diminuant la taille, le triangle bascule car son centre de gravité n'est plus positionné correctement. On peut déplacer le cylindre vers la droite mais alors pour conserver l'horizontalité, celui-ci doit être plus gros. Il faut donc trouver le cylindre dont le centre est sur la perpendiculaire à (AC) passant par F le centre de gravité du triangle et tangent à (AC) et (Ax).
Je me place dans un repère orthonormé (A, Ax, AB).
Cherchons F tout d'abord. Celui-ci est à 2/3 d'une des médianes en partant du sommet. En choisissant la médiane issue de A, on trouve immédiatement que les coordonnées de F sont (1, 2/3).
La droite (AC) a pour équation y=(1/3)x.
La droite (FG) a donc pour équation: y=-3x+c (produit des coeffs directeurs=-1).
F(1,2/3) appartient à (FG) donc: 2/3=-3x1+c et c=11/3.
(FG) a donc pour équation: y=-3x+11/3. (1)
H est le centre du cercle représentant le cylindre.
H est sur la bissectrice de l'angle entre (AC) et (Ax).
La pente de (AC) vaut 1/3. Je note x l'angle entre la bissectrice et (Ax) et X=tan(x).
En utilisant [latex]tan2x=\dfrac{2tanx}{1-tan^2x}[/latex], on trouve [latex]\dfrac13=\dfrac{2X}{1-X^2}[/latex].
Soit [latex]X=\sqrt{10}-3[/latex].
L'équation de la droite (AH) est donc [latex]y=(\sqrt{10}-3)x[/latex].
Le point H est l'intersection de (AH) et (FG) dont l'équation est donnée en (1).
On trouve comme coordonnées: [latex](\dfrac{11\sqrt{10}}{30}, \dfrac{110-33\sqrt{10}}{30})[/latex].
Cette dernière valeur est le rayon du cylindre:
[latex]\dfrac{110-33\sqrt{10}}{30}[/latex] et vaut approximativement 0,188.
Lorsque l'on fait tendre BC vers l'infini, le rayon du cylindre tend vers 1/6.
J'espère ne pas m'être trompé dans les calculs. Je n'ai rien trouvé de plus simple.
Merci pour l'énigme.
#6 - 28-03-2011 16:43:58
- franck9525
- Elite de Prise2Tete
- Enigmes résolues : 48
- Messages : 1935
- Lieu: 86310
Équuilibre précaire
Edit: message modifié suite aux remarques.
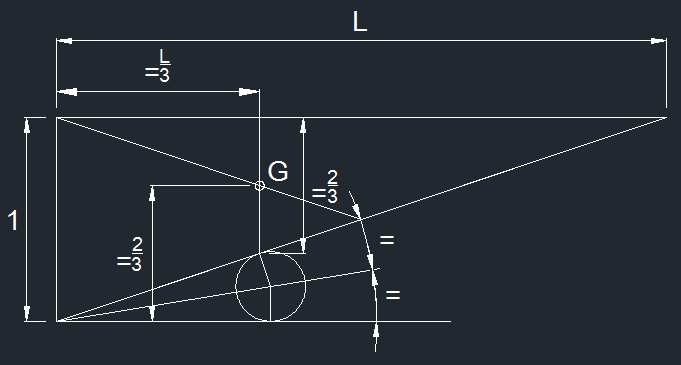
Le centre de gravité se trouve sur la médiane y=1-x/L, à 1/3 de la hauteur ici de longueur L. Les coordonnées de G sont x=2/3 et y=L/3.
Le cylindre supporte le triangle au point tangent avec l’hypoténuse, son diamètre est donc légèrement supérieur à la valeur de 1/3.
Nous avons [latex]\frac 1 3 = R + R cos (atan \frac 1 L) = R \frac{ L + \sqrt {1+L^2}}{\sqrt {1+L^2}}[/latex]
Ce qui donne
[TeX]R = \frac{L^2+1-L\sqrt{1+L^2}}3[/TeX]
avec L = 3
[TeX]R = \frac{10-3\sqrt{10}}3 \approx 0.171 [/TeX]
Lorsque L est grand, l'angle par rapport à la verticale tend vers 0 et donc R vers 1/6.
The proof of the pudding is in the eating.
#7 - 28-03-2011 17:34:58
- looozer
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 697
- Lieu: Belgique
Équilibre précarie
Suite à quelques remarques (de SaintPierre et Jackv, je signale que le point A est totalement antidérapant (on peut rêver!)
mitsuidewi : R=(1-x)/2 n'est pas juste : en zoomant tu verras un petit espace entre le diamètre vertical du cylindre et le segment le longueur x
halloduda : Bien joué! 
Jackv : remarque pertinente!
rivas : je pense que ta condition d'équilibre au départ est trop exigeante, du coup ton rayon est trop grand.
franck9525 : je ne comprends pas d'où vient ton équation "0=..."
#8 - 28-03-2011 18:23:37
- Franky1103
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 3238
- Lieu: Luxembourg
Équilibre rpécaire
Bonjour,
1°) Soit D le point de contact entre le triangle et le cercle.
Soient a l'angle BCA et R le rayon recherché.
R = AD x tg(a/2) et tg a = 1/3
Grâce à la relation tg a = 2 x tg (a/2) / ( 1 - tg2 a), on en déduit:
tg(a/2) = -3+V10 (équation du second degré)
Il reste à trouver AD.
Soit E l'intersection entre la droite BC et la parallèle à AB passant par D.
Le moment des surfaces ABED et DEC par rapport à DE doivent être identiques: on trouve DE = (-1+V5)/2
La relation AD/V10 = (3-V5)/2 (triangles semblables) donne: AD = (3V10-5V2)/2
Finalement R = (-3+V10)(3V10-5V2)/2 = (30+15V2-10V5-9V10)
soit R = 0,196 environ
2°) Le fait d'éloigner C vers l'infini ne change pas les proportions du problème.
Je crois que cela s'appelle une homothétie (mais mes souvenirs sont lointains).
Et donc R reste inchangé à la valeur précédente.
Bonne soirée.
Frank
Edit: Evidemment, quel âne suis-je: il ne faut pas équilibrer les surfaces, mais le moment de celles-ci par rapport à l'axe: je modifie mon texte. Est ce correct ?
#9 - 28-03-2011 19:09:51
- looozer
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 697
- Lieu: Belgique
Équliibre précaire
mitsuidewi, franck9525 et franky1103 : vous placez mal le centre de gravité du triangle, il n'est pas sur le segment vertical que vous avez choisi.
#10 - 28-03-2011 19:15:52
- rivas
- Elite de Prise2Tete
- Enigmes résolues : 48
- Messages : 1106
- Lieu: Jacou
Équilibre prcéaire
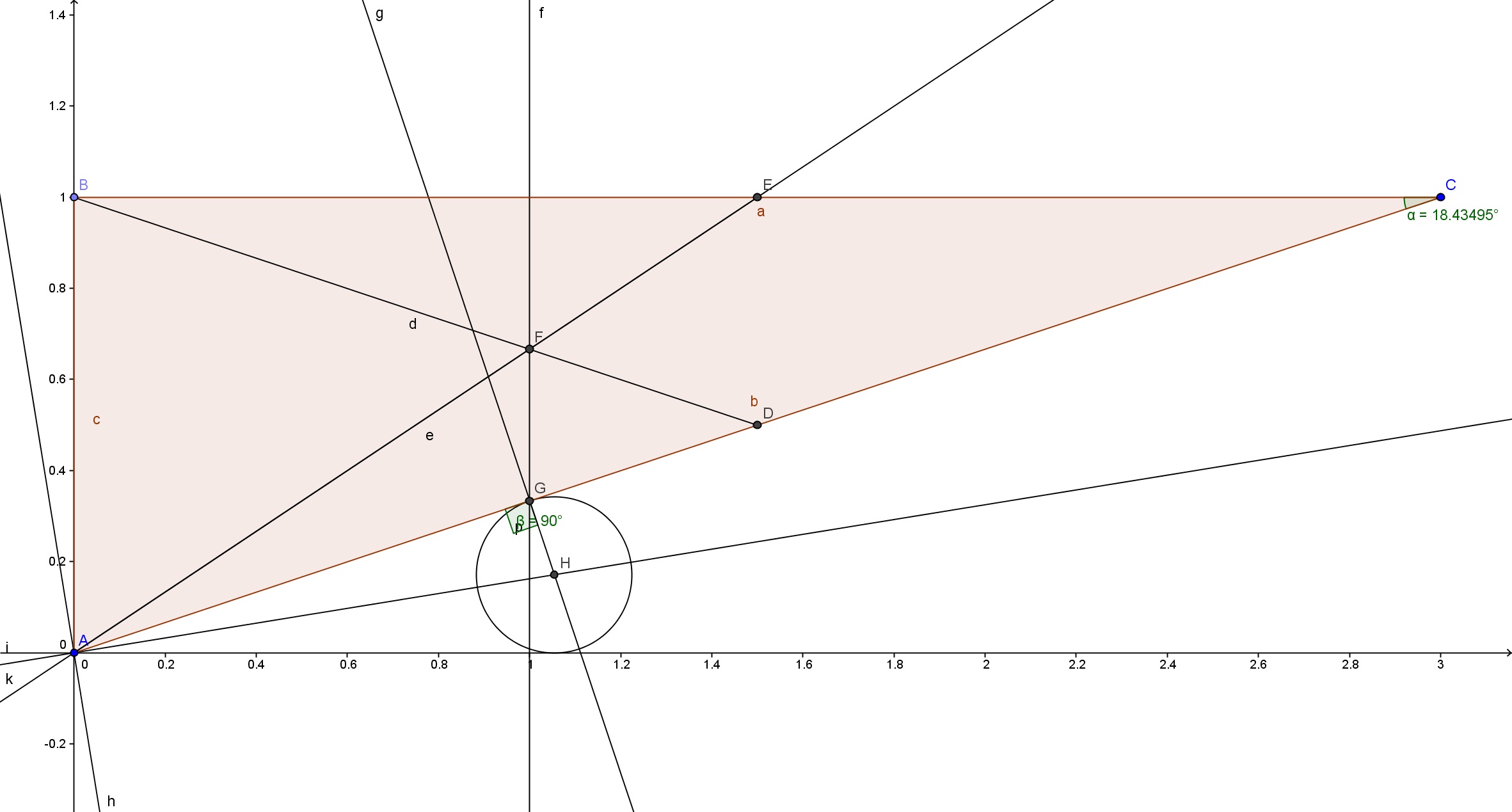
Voir le début des calculs dans mon post précédent.
Une autre possibilité d'équilibre est que le centre de gravité (F dans mon dessin) soit à la verticale du point de contact (G dans mon dessin).
Dans ce cas G a pour coordonnées (1, 1/3).
Le cercle (vue en coupe du cylindre) a son centre sur la bissectrice de (AC) et (Ax) et est tangent à (AC) en G donc a son centre sur la perpendiculaire à (AC) en G (droite (g)).
L'équation de (g) est y=-3x+c (produit des coeffs directeurs=-1).
G(1,1/3) appartient à (FG) donc: 1/3=-3x1+c et c=10/3.
(g) a donc pour équation: y=-3x+10/3. (1)
On a vu que l'équation de la bissectrice est: [latex]y=(\sqrt{10}-3)x[/latex] et on cherche le point H intersection de cette bissectrice avec (g).
On trouve comme coordonnées: [latex](\dfrac{\sqrt{10}}3,\dfrac{10-3\sqrt{10}}3)[/latex]
L'ordonnée de H est le rayon du cercle qui est donc de [latex]\dfrac{10-3\sqrt{10}}3=\dfrac{10}3-\sqrt{10}[/latex] soit approximativement 0,171.
Lorsque l'on fait tendre BC vers l'infini, le rayon du cylindre tend vers 1/6.
J'espère que c'est bon cette fois-ci. 
#11 - 29-03-2011 18:05:16
- L00ping007
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 2010
- Lieu: Paris
Équilibre prévaire
Avec BC=n et R le rayon du cylindre, je trouve :
[TeX]R=\frac{\sqrt{n^2+1}}{3\left(n+\sqrt{n^2+1}\right)}[/TeX]
Application numérique : [latex]R \approx 0,171[/latex]
Et la valeur limite lorsque n tend vers l'infini est :
[TeX]R_{\infty}=\frac16[/TeX]
#12 - 29-03-2011 22:20:26
- looozer
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 697
- Lieu: Belgique
Équuilibre précaire
franck9525, rivas et L00ping007 : bonnes réponses 
Jackv : je t'ai oublié dans la liste des bonnes réponses, veux-tu bien m'en excuser!
#13 - 30-03-2011 17:41:09
- dylasse
- Professionnel de Prise2Tete
- Enigmes résolues : 21
- Messages : 381
Équilubre précaire
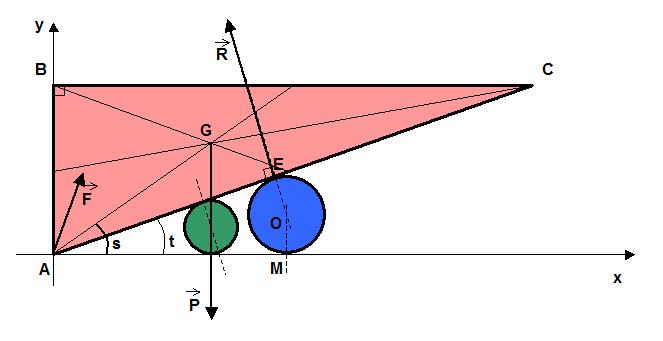
Notre triangle est soumis à 3 forces :
P, son poids, R la réaction du cylindre, perpendiculaire aux surfaces de contact et F la réaction du sol.
Pour que le triangle soit en équilibre, il faut que :
+ la somme des 3 forces soit nulle.
+ la somme des moments de ces forces soit nulle.
Le moment en A de F est nul, donc on a AG ^ P + AE ^ R = 0 (produit vectoriel).
Avec les notations du dessin : AG.P.cos(s) - AE.R.cos(t) = 0, d'où R.cos(t) = AG/AE.P.cos(s).
D'après la somme nulle des forces, on peut calculer la composante verticale de F : yF = P - R cos(t) = P (1 - AG/AE.cos(s)).
Cette composante doit être positive (F dirigé vers le haut), donc AE > AG cos(s).
rem : on ne prend pas en compte la composante horizontale de F, car la "super adhérence" de F signifie que le cone de frottement de F est d'angle plat).
La limite de la position de E pour avoir équilibre est donc AE = AG cos(s).
Par construction AE=AM, donc la position d'équilibre correspond à un cercle vérifiant : AM=AG cos(s), donc M à la verticale de G. Le cercle "vert" correspond à cette position.
Sur le cercle « vert » :
xM = xG = 1/3 xC (position du barycentre)
yM = 0
xO = xM = 1/3 xC
yO = r (rayon du cercle)
(1) xE = xO - sin(t) r = 1/3 xC - r yC/AC
(2) yE = yO + cos(t) r = r (1+xC/AC)
mais aussi, on a E appartient à la droite AC :
yE/xE = yC/xC, donc yE = yC/xC.xE
soit (d'après (2)): yC/xC.xE = r (1+xC/AC) donc : xE= r (1 + xC/AC) xC/yC
on remplace dans (1) : r (1 + xC/AC) xC/yC = 1/3 xC - r yC/AC
D'où : r ((1 + xC/AC) xC/yC +yC/AC)=1/3 xC
ou : r = 1/3 xC.yC/(xC+AC) = 1/3 xC.yC/(xC+rac(xC²+yC²)
A.N. pour xC=3 et yC=1, r=rac(10)-3 = 0,16227766
Pour étudier r lorsque xC tend vers l’infini, on va écrire :
r = 1/3 yC / (1+racine(1+(yC/xC)²), donc r tend vers 1/6 yC= 1/6
#14 - 31-03-2011 21:52:07
- looozer
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 697
- Lieu: Belgique
Équilibre préccaire
Merci à tous d'avoir participé 
Je vous avoue être quelque peu perplexe.
En imaginant cette énigme, je n'avais pas vraiment vu venir la divergence des raisonnements qui seraient proposés.
Je pensait qu'elle pourrait se résumer à chercher le point de l'hypoténuse à la verticale du centre de gravité, car le "cercle" étant fixe, ce point de contact fait office de point d'appui. Restait à chercher le cercle tangent en ce point.
Et puis Jackv et dylasse me sortent des considérations plus orientées "physique" et j'ai envie de les croire également.
La limite à l'infini est clairement 1/6 pour tout le monde, mais pour la première...
En gros j'ai des doutes et j'aimerais vous encourager à donner votre avis maintenant que les réponses de chacun apparaissent.
#15 - 02-04-2011 08:17:50
- dylasse
- Professionnel de Prise2Tete
- Enigmes résolues : 21
- Messages : 381
Équilibre précaite
En relisant ce que Jacky a écrit et ce que j'ai écrit, je suis plus convaincu par Jacky...
En effet, il prend en compte l'équilibre du cylindre, soumis à 2 forces (on peut négliger son poids) et donc trouve la direction de R alors que moi je la suppose perpendiculaire au contact, ce qui est incompatible avec l'équilibre du cylindre....
Les joies et merveilles des maths font qu'au final, je trouve la même conclusion que Jacky : l'équilibre limite correspond au contact du cylindre au sol à la vertical du centre de gravité du triangle, mais je n'ai pas pris le bon chemin.
Je tiens aussi à remercier Jacky pour son schéma 1 et le point O, qui a été pour moi une seconde révélation : quand un solide, soumis à 3 forces, est à l'équilibre, ces 3 forces sont concourrantes (sinon, le moment par rapport à l'intersection de 2 d'entre elles ne serait pas nul pour la troisième...). Eurekâ !
Et merci à Loozer de nous faire prendre la tête !
#16 - 03-04-2011 17:15:28
- Jackv
- Elite de Prise2Tete
- Enigmes résolues : 34
- Messages : 3614
- Lieu: 94110
Équimibre précaire
Un grand merci à dylasse pour ses compliments. 
Je pense même maintenant que l'on peut aller encore plus loin que je ne l'ai été.
En supposant que le point A soit sur un appui vertical, le frottement sur cet appui conduirait à une force FA dirigée vers le bas et faisant un angle = arctg (f) avec l'horizontale.
Cela conduirait à un diamètre encore un peu plus petit que celui que j'ai proposé ! 
Mots clés des moteurs de recherche
|
 |

 Accueil
Accueil
 Forum
Forum












