Forum dédié aux énigmes et à toutes formes de jeux de logique. | Déconnexion |
|
Tu n'es pas identifié sur Prise2tete : s'identifier.  Accueil Accueil
 Forum Forum
|
 |
#1 - 25-05-2011 19:00:37#0 Pub#2 - 25-05-2011 22:09:03
Remplissaeg du plan : plan BAppelons cercle épointé un cercle sur lequel il manque un point. Un mathématicien complet est topologiquement fermé! #3 - 25-05-2011 22:25:09#4 - 25-05-2011 22:41:40#5 - 25-05-2011 23:16:16
Remplissage du plan :: plan BJ'ai répondu trop vite... C'est toujours en faisant la preuve qu'on se rend compte de là où ça coince. #6 - 26-05-2011 08:45:02
Remplissage du plan : lpan B
C'est faux ou je n'ai rien compris #7 - 26-05-2011 12:55:14
remplissage dy plan : plan b*lit le topic Plan B* Podcasts Modern Zeuhl : http://radio-r2r.fr/?p=298 #8 - 26-05-2011 13:48:28
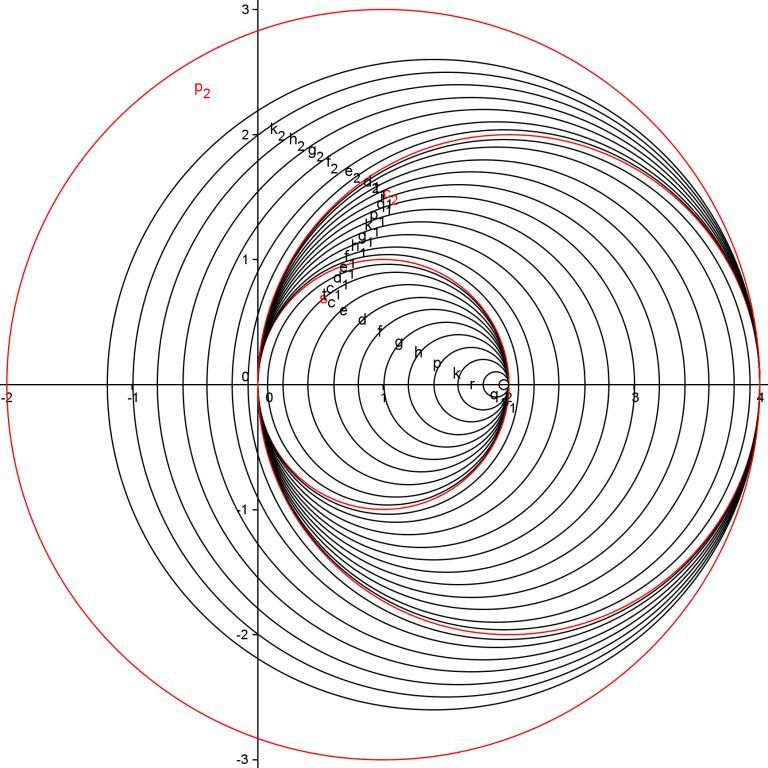
remplissagz du plan : plan bOui mais la figure d'Irmo est jolie. S'il y avait de la couleur, on pourrait croire à un Vasarely. #9 - 26-05-2011 15:33:35
remplisdage du plan : plan bS'il-te-plaît. Je viens d'Aix-en-Provence, alors qu'on ne me bassine plus avec Vasarely, parce que leur musée à la noix, ça va cinq minutes, mais se faire polluer les yeux matin et soir par ce truc, c'est horrible Podcasts Modern Zeuhl : http://radio-r2r.fr/?p=298 #10 - 26-05-2011 16:39:16
rrmplissage du plan : plan bVasimolo il n'y a pas deux cercles tangents mais seulement une droite tangente Un mathématicien complet est topologiquement fermé! #11 - 26-05-2011 17:26:07#12 - 26-05-2011 17:50:58
templissage du plan : plan b
Un mathématicien complet est topologiquement fermé! #13 - 26-05-2011 17:55:43#14 - 26-05-2011 18:05:34
Repmlissage du plan : plan B
En quoi l'inexistence d'un tel cercle empêche le recouvrement ? Peux-tu préciser un peu ton cheminement ????? #15 - 26-05-2011 18:34:10
remplissage du plan : plan nJe me suis pas embêté à faire ma figure pour rien. #16 - 26-05-2011 18:43:19#17 - 27-05-2011 00:03:05
Remplissage du plan : lan BOui j'avais faux. J'avais admis deux choses : Un mathématicien complet est topologiquement fermé! #18 - 27-05-2011 00:20:29#19 - 27-05-2011 02:40:18
relplissage du plan : plan bJ'ai utilisé geogebra. Mais c'est la première fois que je l'utilise, alors je maitrise pas trop encore. #20 - 27-05-2011 08:05:25#21 - 27-05-2011 11:01:36
Remplissage du paln : plan B
J'utilise principalement Declic et Geogebra tous deux téléchargeables gratuitement sur la toile Réponse rapideSujets similaires
Mots clés des moteurs de recherche |
 | ||||||||||||||||||||||||||||||
| Prise2Tete Forum Statistiques Liste des membres Hall of Fame Contact | ||||||||||||||||||||||||||||||||
Un jeu où seules la réflexion, la logique et la déduction permettent de trouver la solution.