Enigme Le plan colorié @ Prise2Tete

Hamilkar · #1

Un plan, donc infini, est colorié en deux couleurs d'une manière quelconque,
c'est à dire qu'on sait seulement ceci : n'importe quel point du plan est colorié
d'une couleur ou de l'autre.
Prouvez qu'il existe deux points situés à exactement un kilomètre de distance, qui sont de la même couleur.

racine · #2

Je vois bien une démonstration par l'absurde.

Hamilkar · #3

J'y ai pensé aussi.

LeSingeMalicieux · #4

Ben si on prend un triangle équilatéral de côté 1km, on aura forcément deux sommets qui pointent deux endroits de couleur identique !
CQFD

Hamilkar · #5

Il n'est pas dit de quelle manière est repartie la couleur, le triangle peut avoir
un sommet vert et un autre bleu par exemple.
"N'importe quel point peut être d'une couleur ou d'une autre".

kosmogol · #6

Et le 3e point il est de quelle couleur ?

Hamilkar · #7

Effectivement j'ai du sauter un truc de mon énoncé là

Vasimolo · #8

C'est plus amusant avec trois couleurs

Vasimolo

kosmogol · #9

Je te reconnais bien là

LeSingeMalicieux · #10

En posant des triangles équilatéraux à l'infini (en formant des hexagones), on peut toujours avoir les trois sommets de tous les triangles de couleurs différentes.
Aussi, je serais tenté de dire qu'il est possible, avec un plan de trois couleurs, qu'on ne puisse jamais trouver deux points distants d'un kilomètre qui soient de la même couleur.

Ton avis Vasimolo ?

Vasimolo · #11

Pas d'accord

Fais tourner ton réseau autour d'un des points

Il me semble avoir déjà vu ce problème sur le site !!!

Vasimolo

MthS-MlndN · #12

Moi, en tout cas, je me galère sur ce problème sans rien trouver, ni dans un sens, ni dans l'autre -_-'

@Vasimolo : je ne vois pas ce que tu veux dire... Je suis un peu con, je crois.

Vasimolo · #13

Il n'y a pas de cons ici ( sauf moi peut-être )

Ce n'est pas trop difficile mais je détaillerais si personne ne trouve ( ce que je ne peux pas croire )

Vasimolo

franck9525 · #14

MthS-MlndN · #15

Euh... Tu plaisantes, la ?

LeSingeMalicieux · #16

Je crains que tes triangles ne soient pas équilatéraux...
Avec des triangles équilatéraux, on forme un hexagone, et non un pentagone.

MthS-MlndN · #17

C'est pour ça que je me suis dit que c'était forcément une blague

LeSingeMalicieux · #18

Venant de toi, je ne m'étais pas posé la question ^^
Faudrait que tu soies sacrément bourré pour ne pas le remarquer !

Vasimolo · #19

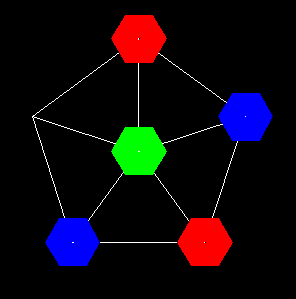
Un dessin qui devrait m'éviter de longues explications .

Vasimolo

MthS-MlndN · #20

@Gasole : tous les points de ton premier cercle ne sont pas forcément de la même couleur, donc ta démo est fausse, je pense...

@Vasimolo : OK, en lisant ton schéma de droite a gauche, j'ai compris l'astuce. Joli

Azdod · #21

Vasimolo; peux tu expliquer ton dessin svp

debutant1 · #22

supposons l’hypothèse H1 aucun point distant de 1km ne soit de la même couleur.

soit O un point rouge, tous les points M situés sur la circonférence du cercle C centré en O de rayon 1 km sont donc bleus.

deux points M1,M2 sur cette circonférences tq M1M2=1km. Ces deux points sont bleus, donc H1 est faux

gasole · #23

@mathias : j'ai supprimé mon post, j'avais pas compris que la question s'était déplacée sur un problème à 3 couleurs...

Supposons par l'absurde que 3 couleurs suffisent pour colorer le plan de telle façon que n'importe quels deux points distants de 1 soient toujours de couleur différente.

Soient A et B, deux points distants de [latex]\sqrt 3[/latex], C le milieu de (AB).
On trace la médiane à (AB) et sur cette médiane, on considère le segment (DE) de longueur 1 et de centre C.

Pythagore nous assure que les triangles (A,D,E) et (B,D,E) sont équilatéraux et de côté 1. Forcément A et B doivent être de la même couleur.

Conclusion intermédiaire : puisque A et B étaient quelconques, deux points distants de [latex]\sqrt 3[/latex] sont de la même couleur.

Soit maintenant, un cercle de centre A et de rayon [latex]\sqrt 3[/latex], tous les points de ce cercle sont donc de la même couleur que A, or sur cette circonférence, on peut en trouver deux (F et H) distants entre eux de 1. Contradiction.

En image :

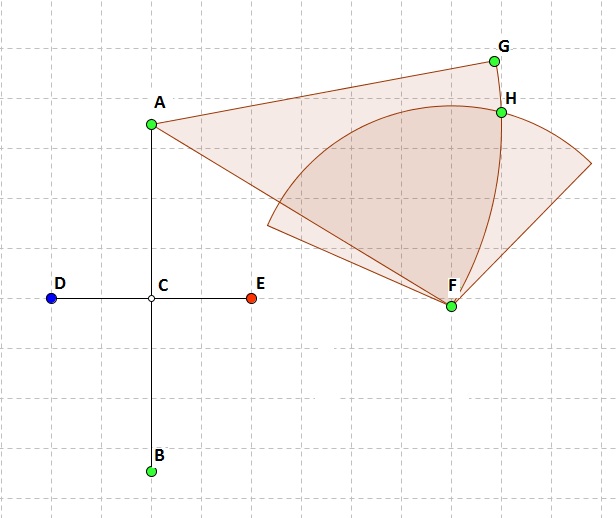
PS : hemm je crois que c'est la même chose que vasimolo

dhrm77 · #24

Puisque pour avoir, dans un plan, 2 points quelconques distants de 1 qui soient toujours de couleurs differentes, ni 2, ni 3 couleurs ne suffisent, alors combien faut-il de couleurs au minimum?

MthS-MlndN · #25

C'est bizarre, je m'attendais a ce que quelqu'un la pose, celle-ci

Forum dédié aux énigmes et à toutes formes de jeux de logique.	Déconnexion
Tu n'es pas identifié sur Prise2tete : s'identifier. Accueil Forum	[+]

#1 - 02-02-2011 17:56:58

ke plan colorié

#0 Pub

#2 - 02-02-2011 17:59:38

lz plan colorié

#3 - 02-02-2011 18:00:27

le plan colotié

#4 - 02-02-2011 18:22:05

ke plan colorié

#5 - 02-02-2011 18:26:22

Le pln colorié

#6 - 02-02-2011 18:31:21

Le plan colori

#7 - 02-02-2011 18:38:43

Le plan clorié

#8 - 02-02-2011 19:04:45

le olan colorié

#9 - 02-02-2011 19:14:21

Le pla colorié

#10 - 02-02-2011 19:35:35

le plan volorié

#11 - 02-02-2011 19:45:53

Le plan coloréi

#12 - 02-02-2011 19:47:14

Le plan clorié

#13 - 02-02-2011 19:59:40

Le plan coloriéé

#14 - 02-02-2011 21:08:29

le plan coloeié

#15 - 02-02-2011 21:12:23

Le plan coloiré

#16 - 02-02-2011 21:13:26

Le pla ncolorié

#17 - 02-02-2011 21:18:14

me plan colorié

#18 - 02-02-2011 21:21:28

Le plan coloiré

#19 - 02-02-2011 22:52:37

le plan colirié

#20 - 03-02-2011 00:26:17

Le plann colorié

#21 - 03-02-2011 01:13:57

L plan colorié

#22 - 03-02-2011 08:47:37

le plan cokorié

#23 - 03-02-2011 09:19:59

le plzn colorié

#24 - 03-02-2011 12:53:02

Le plan collorié

#25 - 03-02-2011 13:02:26

Le plan coloriéé

Réponse rapide

Sujets similaires

Mots clés des moteurs de recherche

Pied de page des forums