[TeX]ln(2)\approx 0.693[/TeX]

Si [latex]U_n[/latex] représente le prix après n années, on a [latex]U_{n+1}=(1+\frac{a}{100})U_n[/latex] où a est le pourcentage.

On sait alors que [latex]U_n=U_0(1+\frac{a}{100})^n[/latex] et on veut n le plus petit tel que [latex]U_n\geq 2U_0[/latex].

Ce qui en passant au log donne: [latex]n\geq \frac{ln2}{ln(1+\frac{a}{100})}[/latex].
Or ln2 vaut a peu près 0,7 et on a x est une bonne approximation de ln(1+x) d'où n environ égal à 70/a.

Merci pour cette énigme.

Soit un taux d'inflation de [latex]k[/latex] pourcent, qu'on suppose constant. Au bout de [latex]N[/latex] années, les prix auront été multipliés par
[TeX]\left( 1 + 0.01 k \right)^N[/TeX]
On veut donc, en fonction de k, trouver N tel que :
[TeX]\left( 1 + 0.01 k \right)^N = 2[/TeX]
On passe au log :
[TeX]N \ln \left( 1 + 0.01 k \right) = \ln(2)[/TeX]
Soit :
[TeX]N = \frac{\ln(2)}{\ln \left( 1 + 0.01 k \right)}[/TeX]
[latex]\ln(2)[/latex] vaut un peu moins de [latex]0.7[/latex], et si [latex]x[/latex] est suffisamment petit, on a [latex]\ln \left( 1 + x \right) \approx x[/latex], ce qui permet de conclure.

Soit n le nombre d'années et t le taux d'inflation.

On veut avoir
(1 +t/100)^n > 2

e^(n*ln (1+t/100))>2

n*(ln (1 +t/100) > ln (2) 

n >  ln (2)/ ln(1 +t/100)

Or on sait que quand t/100 est au voisinage de 0 ln( 1 + t/100) est proche de t/100 (c'est normalement le cas).

et ln(2) vaut environ 0,7  (arrondi au dixième)

bref ln(2) / ln(1 +t/100) vaut environ 70/t ce qui confirme l’hypothèse annoncée.


Un peu trop d'arrondi à mon gout dans cette méthode, je comprend pourquoi l'économie va  si mal si nos maîtres des finances manquent autant de rigueur dans leurs calculs.

Que des bonnes réponses ! bravo à tous !
C'est le cas aussi d'un montant placé à la banque avec un intérêt Composé !

Bonjour,

Au bout de [latex]n[/latex] années d'inflation au taux [latex]\tau[/latex](%) ici supposé constant, un prix [latex]P[/latex] de départ devient :
[TeX]P*(1+\frac{\tau}{100})^n[/TeX]
Un prix double donc quand pour [latex](n, \tau)[/latex], on a  :
[TeX](1+\frac{\tau}{100})^n = 2[/TeX]
Si on prend [latex]n=\frac{70}{\tau}[/latex] comme suggéré, l'expression est bien proche de 2 par le calcul.



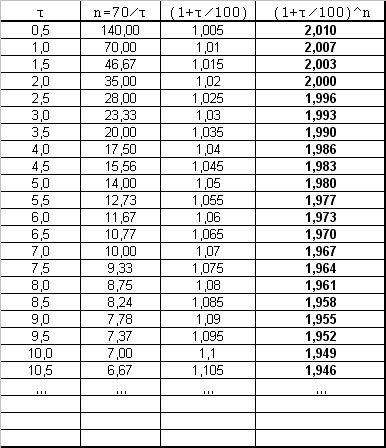
En passant par les logarithmes (ln) ...

On veut donc [latex](1+\frac{\tau}{100})^n = 2[/latex]

soit  [latex]n \ln(1+\frac{\tau}{100}) = \ln(2) [/latex]

comme [latex]\ln(1+\frac{\tau}{100}) >0\ \forall \tau>0[/latex]

On veut donc [latex]n = \frac {\ln(2)}{\ln(1+\frac{\tau}{100})}[/latex]

or [latex]\ln(1+\epsilon) \approx \epsilon [/latex] pour [latex]\epsilon[/latex] au voisinage de 0,


(et même [latex]\ln(1+x) \leq x \ \forall x\geq 0 [/latex] )

Donc pour un taux [latex]\tau[/latex] faible, où [latex]\frac{\tau}{100}[/latex] reste "proche" de 0, le passage par cette approximation permet d'écrire l'expression précédente ainsi :
[TeX]n = \frac {\ln(2)}{(\frac{\tau}{100})}[/TeX]
soit [latex]n = \frac {100\ln(2)}{\tau}[/latex]

or:  [latex]100\ln(2)=69.3147[/latex]

70 > 69 d'où la "règle des 70" [latex]n=\frac{70}{\tau}[/latex]
(dans le domaine de validité de l'approximation du ln)

Merci, à bientôt,