 |
#1 - 26-09-2011 19:26:16
- Promath-
- Elite de Prise2Tete
- Enigmes résolues : 18
- Messages : 1416
- Lieu: Au fond de l'univers
L'îl parfaite.
Monsieur Parfait possède une île parfaitement ronde sur
laquelle sont posées quatre barrières parfaitement droites
reliant quatre points situés sur le bord de l’île. Sur cette
île se trouve un étang rond tangent aux quatre barrières.
Voici les dimensions:
(33 mètres et 77 mètres) ainsi que
l’angle formé par ces barrières
(135°).
Quelle est la longueur de la barrière
AB ?
Si besoin est, on prendra 1,414 pour √2, 1,732 pour √3 et
3,1416 pour p et on donnera la réponse arrondie au mètre
le plus proche.
Bonne chance!
PS: Spoiler : [Afficher le message] AD=33
DC=77
CB=?
AB= A TROUVER
Un promath- actif dans un forum actif
#2 - 26-09-2011 20:48:40
- golgot59
- Elite de Prise2Tete
- Enigmes résolues : 48
- Messages : 1494
- Lieu: Coutiches
l'île pargaite.
Je ne vois pas, ne manque-t-il pas une donnée ?
J'ai l'impression que l'étang peut avoir un rayon variable...
Je vais essayer...
#3 - 27-09-2011 12:09:31
- esereth
- Professionnel de Prise2Tete
- Enigmes résolues : 49
- Messages : 176
L'îîle parfaite.
Bonjour,
Cette fois j'ai un problème avec la case réponse.
Pour simplifier les calcul j'ai réduit à AD=3 et CD=7. Il sera toujours temps de multiplier par 11 à la fin.
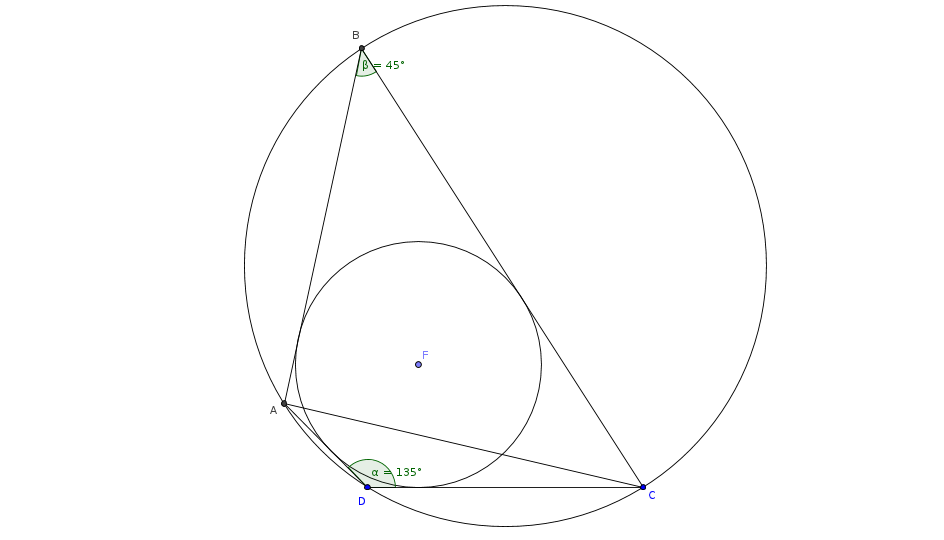
Le théorème de Pitot caractérise les quadrilatères circonscriptibles, c'est-à-dire les quadrilatères dans lesquels on peut construit un cercle tangent à tous les côtés.
Cette condition est simple : [latex]AB + CD = AD + BC[/latex]. (les sommes des côtés opposés sont égales)
Ici elle permet d'écrire [latex]BC=AB+4[/latex].
Le fait que ABCD soit inscrit dans un cercle peut être caractérisé par l'égalité d'angles
[TeX]\widehat{ABC}+ \widehat{ADC} = \pi [/latex] qui donne [latex]\widehat{ABC}= \frac{\pi}{4}[/TeX]
En écrivant la formule d'Al-Kashi dans les deux triangles ADC et ABC, on a deux expressions de [latex]AC^2[/latex] (l'une exacte et l'autre en fonction trinôme de AB)
Dans ADC:
[TeX]AC^2=AD^2+CD^2-2AD.CD\cos \frac{3\pi}{4} = \dots = 58+21\sqrt{2}[/TeX]
Dans ABCen remplaçant BC par AB + 4
[TeX]AC^2=AB^2+(AB+4]^2+2AB(AB+4)\cos \frac{\pi}{4} = \dots = (2-\sqrt{2})AB^2+(8-4\sqrt{2})AB+16[/TeX]
En identifiant :
[TeX] (2-\sqrt{2})(AB^2+4AB)=42+21\sqrt{2}[/TeX]
puis [latex]AB^2+4AB=63+42\sqrt{2}[/latex]
puis finalement à [latex] (AB+2)^2=67+42\sqrt{2}[/latex]
qui donne [latex]AB +2 =7+ 3\sqrt{2} [/latex] càd [latex] AB= 5+ 3\sqrt{2} [/latex]
La réponse attendue est donc [latex]55+33\sqrt{2}[/latex] qu'on peut arrondir à 102
Et au passage on a aussi le quatrième côté qui vaut [latex] 99+33sqrt2 [/latex]
.Je continue pour le plaisir mais avec mes chiffres à moi : 3, 7, [latex]5+3\sqrt2[/latex], [latex]9+3\sqrt2[/latex].
le rayon r du cercle inscrit est facile à calculer en écrivant l'aire de deux manières différentes.[latex]\frac{1}{2}r(AB+BC+CD+DA)=\frac{1}{2}AB \times BC \sin \frac{\pi}{4} + \frac{1}{2}AD \times CD \sin \frac{3\pi}{4} [/latex]
Cela s'écrit en remplaçant et en simplifiant :
[TeX]r(24+6\sqrt2)=42+42\sqrt2[/TeX]
et cela donne [latex]r=\frac{2+3\sqrt2}{2}[/latex]
Pour le rayon du cercle circonscrit R c'est plus compliqué (pas pour le calcul mais pour le résultat  ) )
On a d'après la formule des sinus :
[TeX]\frac{AC}{ \sin \frac {\pi }{4}}=2R[/TeX]
cela donne [latex]R=\sqrt{\frac{58+21\sqrt2}{2}}[/latex]
#4 - 27-09-2011 17:04:59
- Promath-
- Elite de Prise2Tete
- Enigmes résolues : 18
- Messages : 1416
- Lieu: Au fond de l'univers
m'île parfaite.
Bravo!
Pour repondre : xxxxm
Un promath- actif dans un forum actif
#5 - 28-09-2011 09:16:18
- halloduda
- Professionnel de Prise2Tete
- Enigmes résolues : 24
- Messages : 495
- Lieu: Ardèche
L'îel parfaite.
Les bissectrices des 4 angles doivent être concourantes.
Avec un bon outil graphique, on trouve rapidement
AB = 102 m
#6 - 28-09-2011 11:07:11
- NickoGecko
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 1823
l'île parfaute.
Bonjour
Merci pour cette énigme "géométrie"
> Je prends mon tour en ayant fait la figure, mais je dois compléter la solution
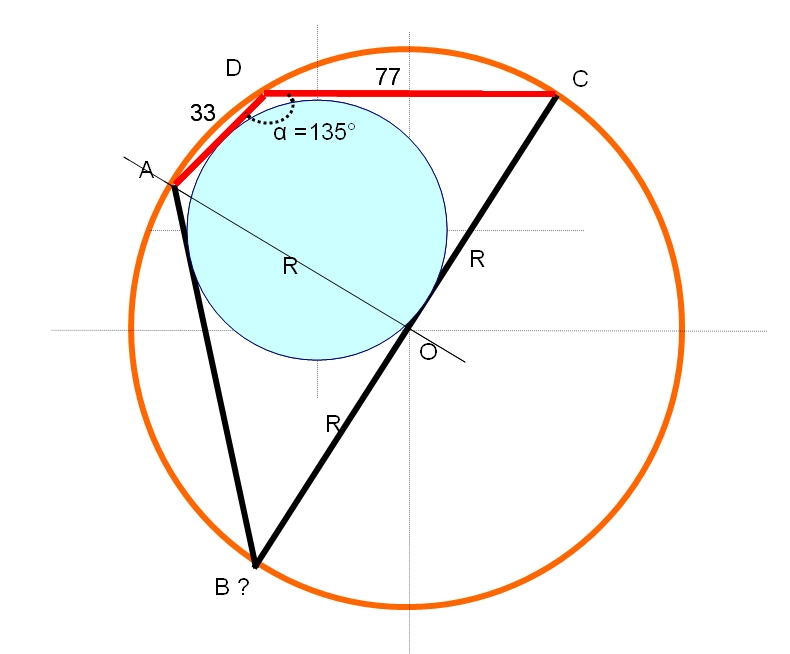
Nous avons, en définissant le cercle circonscrit, de centre O, représentant l'île.
OA=OD=OB=OC=R, rayon de l'île
CB est le diamètre de l'île.
On montre que l'angle AOC est droit
(en effet, AOC + 2 x 135° = 2 x 180°)
On note aussi que l'angle complémentaire en D à 135° est 45°
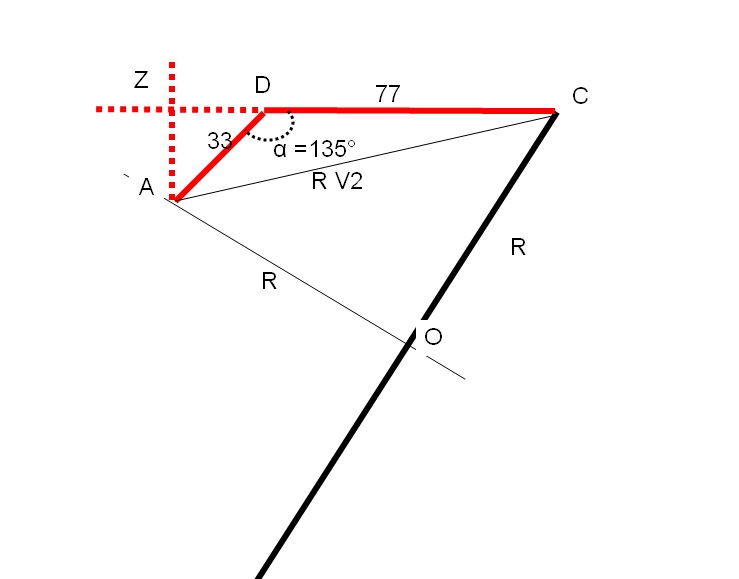
On crée un point Z sur (DC) et ZD = AD cos 45° = AD V2 / 2
AZ = ZD
(V = racine, je ferai du latex plus tard)
d'où (R V2)² = AZ² + (ZD+DC)²
d'où 2R² = (33²/2) + (33V2 / 2 + 77)²
Application numérique R = 74,68 72,84 m
AB = R V2
AB = 105,62 ---> 103,01 m
Il faut trouver la surface de l'étang ? (je cherche ...)
Petit édit du calcul après le chrono au vu des autres réponses, mais je cherche si l'écart avec la réponse attendue 102 m vient du raisonnement de base, d'une erreur dans l'écriture ou encore de l'application numérique finale ....
Merci, A+
Il aurait pu pleuvoir, con comme il est ! (Coluche)
#7 - 28-09-2011 11:08:23
- rivas
- Elite de Prise2Tete
- Enigmes résolues : 48
- Messages : 1106
- Lieu: Jacou
L'île pparfaite.
Je pense qu'il est correct de citer les sources des problèmes.
Dans ce cas, j'ai reconnu le problème n°18 de la finale régionale du 25e Championnat International des Jeux Mathématiques et Logiques (finale régionale qui n'est plus disputée en France depuis quelques années).
L'énoncé disponible par exemple ici donne en plus une figure.
Pour le problème lui-même:
Le plus difficile est de trouver une solution "simple" qui minimise les calculs monstrueux. Voici ce que j'ai trouvé de mieux. Il reste un calcul à la fin qui me semble difficile sans calculatrice....
Je nomme a, b, c, d les longueurs des côtés dans l'ordre de parcours en commençant par la longueur que l'on cherche. Soit D la longueur de la diagonale séparant a et d d'un côté et b et c de l'autre.
On a c=77, d=33. On cherche a.
Le théorème d'Al-Kashi nous donne:
[TeX]D^2=33^2+77^2-2.33.77.cos(135)=7018+2541\sqrt2[/TeX]
Le quadrilatère étant inscrit dans un cercle (et convexe) on sait que l'angle opposé à celui à 135° mesure 45° (180-135).
On a donc aussi (Al-Kashi encore):
[TeX]D^2=a^2+b^2-2ab.cos(45)[/latex] (1)
Mais le quadrilatère est aussi circonscriptible (circonscrit au lac) et le Théorème de Pitot nous dit donc que:
a+c=b+d, soit: b=a+44.
(1) devient donc:
[latex]7018+2541\sqrt2=a^2+(a+44)^2-2a(a+44)\dfrac{\sqrt2}2[/TeX]
qui réduite devient:
[latex]a^2(2-\sqrt2)+a(88-44\sqrt2)-(5082+2541\sqrt2)=0[/latex].
Equation de degré 2 un peu barbare qui admet 2 solutions dont une seule positive qui arrondie au plus près donne 102m, ce qui est validé par la case réponse.
Merci pour cette énigme intéressante.
#8 - 28-09-2011 12:01:28
- Franky1103
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 3238
- Lieu: Luxembourg
L'île parfate.
Bonjour,
A quoi correspondent les dimensions de 33m et de 77m ?
Est ce que ce sont les diamètres de l'étang et de l'île ?
Ou est ce que ce sont les longueurs de 2 des 4 barrières ?
Bonne journée.
Frank
#9 - 28-09-2011 12:25:20
- Promath-
- Elite de Prise2Tete
- Enigmes résolues : 18
- Messages : 1416
- Lieu: Au fond de l'univers
L'le parfaite.
33 et 77 sont la longueurs des 2 barrières...
Un promath- actif dans un forum actif
#10 - 29-09-2011 10:23:06
- Jackv
- Elite de Prise2Tete
- Enigmes résolues : 34
- Messages : 3609
- Lieu: 94110
Lîle parfaite.
Il existe 2 possibilités pour réaliser la construction, soit avec AB < BC, soit avec AB > BC , qui correspondent à une longueur BC et à des diamètres de l'ile et de l'étang différents.
Curieusement, sans que j'ai réussi à en faire la démonstration, la longueur AB reste identique dans les 2 cas :
AB = 101.67 m (102m en arrondissant à l'entier le plus proche)
Bravo pour avoir mis en évidence cette singularité.
#11 - 30-09-2011 14:37:54
- esereth
- Professionnel de Prise2Tete
- Enigmes résolues : 49
- Messages : 176
L'île parfaiite.
@NickoGecko
Je pense que tu as fait une erreur en imaginant que BC est un diamètre. A mon avis O n'est par sur (BC) même s'il n'en est pas loin.
#12 - 30-09-2011 15:04:16
- NickoGecko
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 1823
L'île parfaite..
Merci Esereth !
Mon père me disait bien (quand j'étais petit ...) que la géométrie était l'art de raisonner juste avec des figures fausses !
A la prochaine !
Il aurait pu pleuvoir, con comme il est ! (Coluche)
#13 - 30-09-2011 19:32:05
- Promath-
- Elite de Prise2Tete
- Enigmes résolues : 18
- Messages : 1416
- Lieu: Au fond de l'univers
l'îke parfaite.
rivas a écrit:Je pense qu'il est correct de citer les sources des problèmes.
Dans ce cas, j'ai reconnu le problème n°18 de la finale régionale du 25e Championnat International des Jeux Mathématiques et Logiques (finale régionale qui n'est plus disputée en France depuis quelques années).
L'énoncé disponible par exemple ici donne en plus une figure.
.
Normal, je l'ai proposé à la ffjm qui l'a mis au concours, et je voulais insister sur cette nigme, voilà tout!
Un promath- actif dans un forum actif
#14 - 30-09-2011 23:12:32
- rivas
- Elite de Prise2Tete
- Enigmes résolues : 48
- Messages : 1106
- Lieu: Jacou
l'îme parfaite.
Tu as bien fait d'insister, elle était très bien.
On pourrait d'ailleurs proposer ici plus souvent des énigmes extraites du championnat tout en citant la source je trouve. Elles sont en général ludiques et instructives.
Mots clés des moteurs de recherche
|
 |

 Accueil
Accueil
 Forum
Forum









