Je vais utiliser pour ce problème :
La relation entre les 4 droites remarquables d'un triangle isocèle issues du sommet isocèle(4ème)
Le théorème des milieux (4ème)
Le théorème de Pythagore(3ème)
de la trigonométrie (3ème)
La formule cos(a-b) (1ère S)
La formule de Héron pour calculer l'aire d'un triangle quelconque connaissant les trois longueurs du triangle (1ère S)
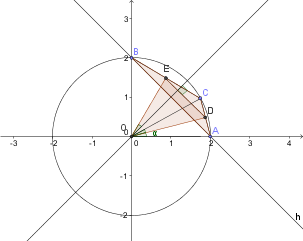
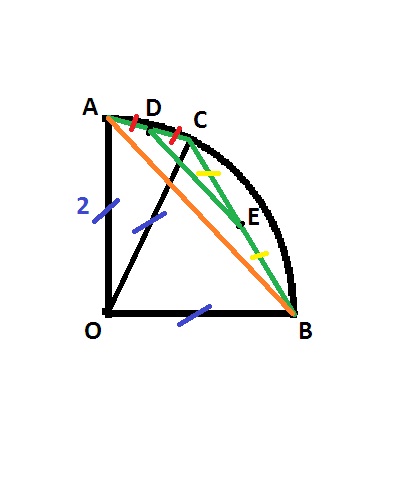
D'après l'énoncé nous savons que OA=OB=2cm
Puisque C appartient au quart de cercle on en déduit OC=2cm
Puisque nous avons un quart de cercle, le triangle OAB est rectangle en O, d'après le théorème de Pythagore on a AB=2 racine de 2
D'après le Théorème des Milieux on en déduit aussi que DE=1/2AB, DE=racine de 2
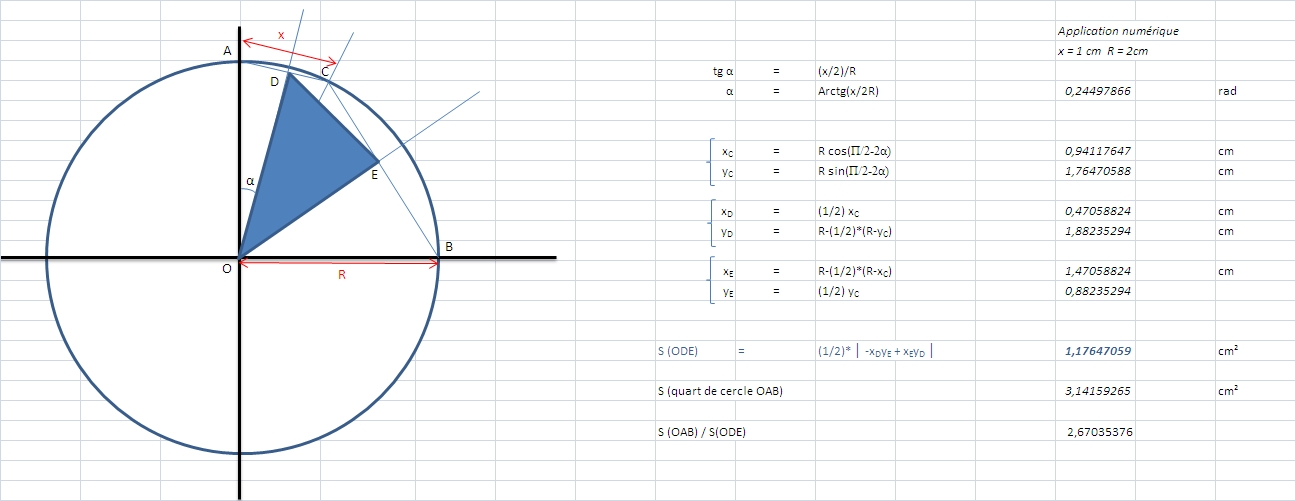
1) Cas où AC=1cm
a)Calcul de OD
D milieux de [AC] donc AD=1/2
Le triangle OAC est isocèle en O, OD est une médiane mais est donc aussi une hauteur.
D'après Pythagore, dans le triangle OAD rectangle en D, on trouve OD=(racine de 17)/2
b)Calcul de OE
*Calcul de l'angle COE
Le triangle OAC est isocèle en O, OD est une médiane mais est donc aussi une bissectrice donc on a :
l'angle AOD=l'angle DOC= Arcsin (1/4) car sin(angle AOD)=AD/AO=(1/2)/2=1/4
Le triangle OBC est isocèle en O, OE est une médiane mais est donc aussi une bissectrice donc on a :
l'angle COE=l'angle EOB, or l'angle AOD+l'angle DOC+l'angle COE+l'angle EOB = 90° donc l'angle AOD+l'angle COE = 45° d'où :
l'angle COE = 45°-Arcsin (1/4)
** Calcul de OE
Le triangle OEC est isocèle en O, OE est une médiane mais est donc aussi une hauteur.
Dans le triangle OEC rectangle en E on a donc :
cos (angle COE) = OE/2
OE = 2 cos(45°-Arcsin (1/4))
OE = 2 (cos45°xcos(Arcsin (1/4)) + sin45°xsin(Arcsin (1/4)))
OE = 2 ( (racine de 2)/2 x cos(Arcsin (1/4)) + (racine de 2)/2 x 1/4 )
or puisque cos²a + sin²a =1 alors cos²(Arcsin (1/4) = 1-(1/4)² = 15/16 d'où
cos(Arcsin (1/4) = (racine de 15)/4
On a donc OE = 2 ( (racine de 2)/2 x (racine de 15)/4) + (racine de 2)/2 x 1/4 )
OE = ( (racine de 30)+(racine de 2) )/4
c)Calcul de l'Aire du triangle ODE
Grâce à la formule de Héron puisque nous connaissons les 3 côtés du triangle ODE nous pouvons en déduire son aire.
Formule de Héron:( Aire ODE )² = s(s-OD)(s-OE)(s-DE) avec s=1/2(OD+OE+DE)
Je n'effectue pas le calcul qui n'a que pour intérêt mettre des nombres dans tous les sens et alourdir mon message.
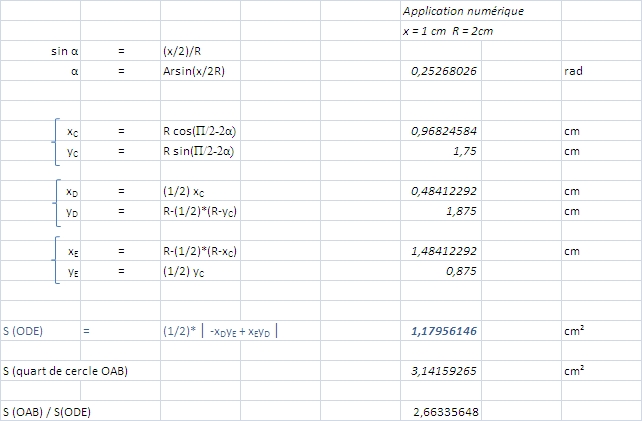
2) Cas où AC=x cm
a)Calcul de OD
D milieux de [AC] donc AD=(1/2)x
Le triangle OAC est isocèle en O, OD est une médiane mais est donc aussi une hauteur.
D'après Pythagore, dans le triangle OAD rectangle en D, on trouve OD=(racine de (16+x²))/2
b)Calcul de OE
*Calcul de l'angle COE
Le triangle OAC est isocèle en O, OD est une médiane mais est donc aussi une bissectrice donc on a :
l'angle AOD=l'angle DOC= Arcsin ((1/4)x) car sin(angle AOD)=AD/AO=((1/2)x)/2=(1/4)x
Le triangle OBC est isocèle en O, OE est une médiane mais est donc aussi une bissectrice donc on a :
l'angle COE=l'angle EOB, or l'angle AOD+l'angle DOC+l'angle COE+l'angle EOB = 90° donc l'angle AOD+l'angle COE = 45° d'où :
l'angle COE = 45°-Arcsin ((1/4)x)
** Calcul de OE
Le triangle OEC est isocèle en O, OE est une médiane mais est donc aussi une hauteur.
Dans le triangle OEC rectangle en E on a donc :
cos (angle COE) = OE/2
OE = 2 cos(45°-Arcsin ((1/4)x))
OE = 2 (cos45°cos(Arcsin ((1/4)x)) + sin45°sin(Arcsin ((1/4)x)))
OE = 2 ( (racine de 2)/2 cos(Arcsin ((1/4)x)) + (racine de 2)/2 (1/4)x )
or puisque cos²a + sin²a =1 alors cos²(Arcsin ((1/4)x) = 1-((1/4)x)² = (16-x²)/16 d'où
cos(Arcsin (1/4) = (racine de (16-x²))/4
On a donc OE = 2 ( (racine de 2)/2 (racine de (16-x²))/4 + (racine de 2)/2 (1/4)x )
OE = ( (racine de 2) (racine de (16-x²) + x) ) / 4
c)Calcul de l'Aire du triangle ODE
Grâce à la formule de Héron puisque nous connaissons les 3 côtés du triangle ODE nous pouvons en déduire son aire.
Je ne suis pas maso au point de me retrouver avec des calculs interminables et des x dans tous les sens.

 Accueil
Accueil
 Forum
Forum