 |
#1 - 21-07-2012 20:47:58
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,426E+3
Crayoon sur une étagère
Bonsoir à tous 
J'ai rangé mon crayon rouge dans une boîte cylindrique que j’ai posée sur une étagère . Je me rend compte alors que je ne peux pas sortir le crayon sans bouger la boîte .

Exprimer à l'aide des longueurs e , h et d la taille minimale c du crayon ?
Vasimolo
PS : Question initiale ( sans intérêt ) : il paraît que cette situation ne peut pas se produire si le crayon est posé dans un dé .
#2 - 21-07-2012 23:29:59
- looozer
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 697
- Lieu: Belgique
Crayon ssur une étagère
Pas besoin des dimensions du dé par rapport à celles du cylindre et/ou du crayon et/ou de l'étagère?
Il manque quelque chose ou je n'ai pas compris le problème.
#3 - 22-07-2012 01:01:40
Crayno sur une étagère
ne manquerait il pas une hypothese dans ce probleme: en supposant un crayon d'epaisseur nulle qui rentre juste dans la boite dans la position la plus favorable( par exemple dont la longueur vaut une grande diagonale du cube) et une boite qui arrive au ras de la partie superieure de l'etagere moins epsilon ,le crayon ne sortira pas si l'angle qu'il fait avec le plan horizontal est superieur a zero.
a moins qu'il faille faire des hypotheses sur la longueur du crayon alors la je veux bien reprendre le probleme.
#4 - 22-07-2012 01:45:54
- shadock
- Elite de Prise2Tete
- Enigmes résolues : 39
- Messages : 3334
crayon sur ine étagère
Trivial ? Dans un cube le crayon épouse un arc de cercle de rayon le côté du cube.
Shadock 
"L'expérience est une lanterne qui n'éclaire que celui qui la porte." L-F. Céline
#5 - 22-07-2012 01:53:08
- SHTF47
- Imprnnçbl de Prs2Tt
- Enigmes résolues : 39
- Messages : 1629
- Lieu: Autre nom du colin
Crayon sur nue étagère
Une histoire de racine de 3, à tout hasard ?
La musique est une mathématique sonore, la mathématique une musique silencieuse. [Edouard HERRIOT]
#6 - 22-07-2012 11:56:37
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 5,985E+3
crayon sur unz étagère
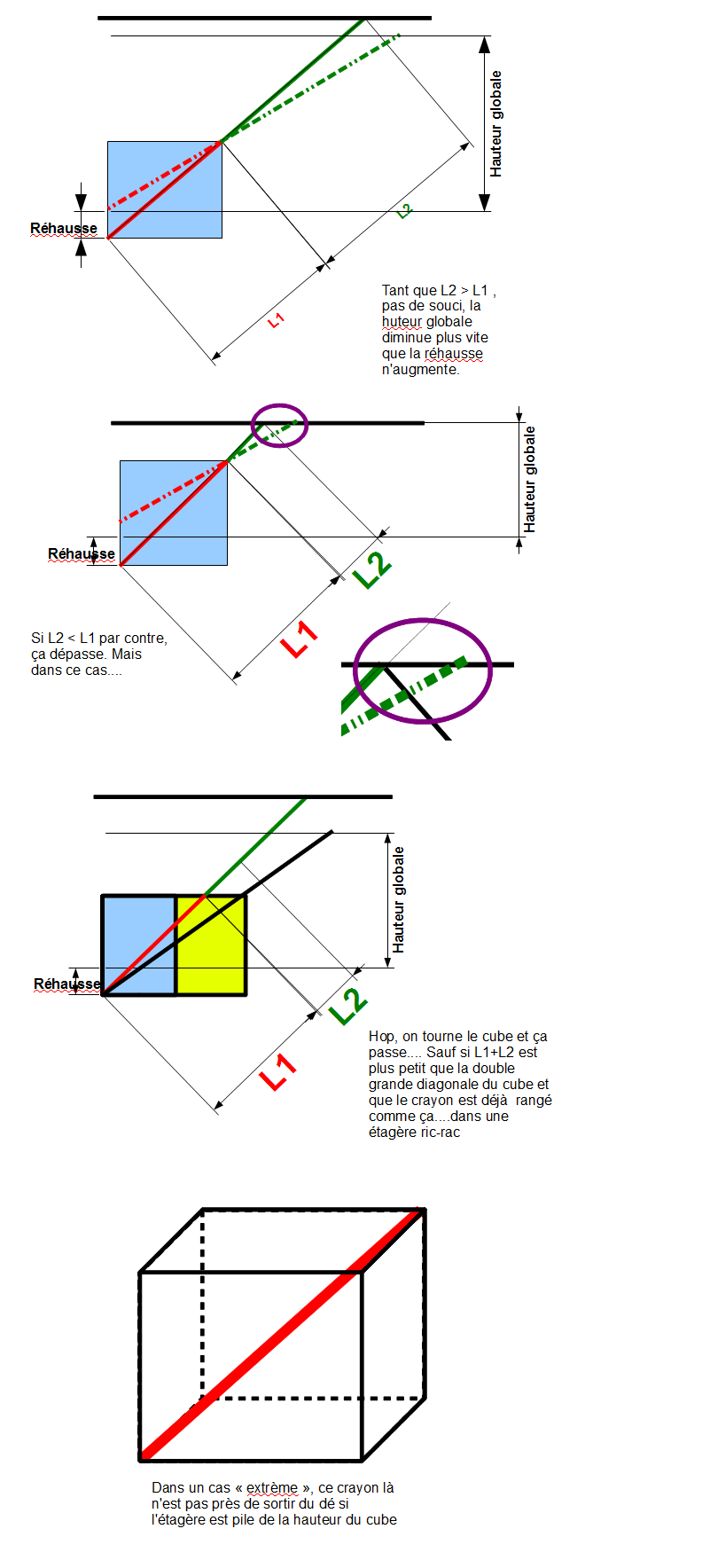
Je n'ai pas bien tout compris alors j'ai fait tous les cas ... Si le cube fait la même hauteur que le cylindre, aucun souci.
Si c'est juste "peut-on sortir un crayon d'un cube, la réponse est non, je pense...
#7 - 22-07-2012 12:51:34
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,426E+3
crauon sur une étagère
Je me suis manifestement et magnifiquement planté dans mes calculs et l'énigme perd beaucoup de son intérêt 
Je rends les réponses visibles , je vais essayer de corriger le problème pour faire apparaître une curiosité que j'ai observée .
Désolé pour ceux qui ont perdu un peu ou beaucoup de leur temps 
Vasimolo
#8 - 22-07-2012 14:24:44
- looozer
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 697
- Lieu: Belgique
crayon sur yne étagère
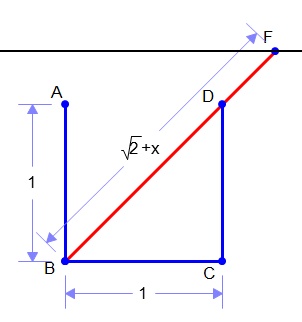
Considérons un dé d'arête 1 et un crayon de longueur [latex]\sqrt{2}+x[/latex]
Dans la situation la plus défavorable (image 1), l'étagère est à hauteur de l'extrémité supérieure du crayon : [latex]\frac{\sqrt{2}+x}{\sqrt{2}}[/latex]
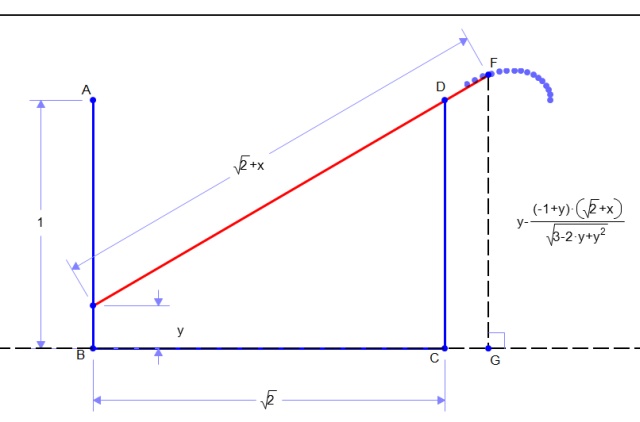
En déplaçant le crayon selon la grande diagonale du dé (image 2), son extrémité supérieure est à une hauteur de [latex]$y-\dfrac{(-1+y)\cdot \left (\sqrt{2}+x\right )}{\sqrt{3-2\cdot y+y^{2}}}$[/latex] (y est la hauteur de l'extrémité inférieure du crayon)
Cette extrémité décrit une courbe style strophoïde dont il faut nous assurer que le maximum local ne dépasse pas [latex]\frac{\sqrt{2}+x}{\sqrt{2}}[/latex]
Ce maximum est atteint pour y = [latex]1+\sqrt{-2+2^{2/3} \left(2+2 \sqrt{2} x+x^2\right)^{1/3}}[/latex]
à une hauteur h(x) = [latex]1+\sqrt{-2+2^{2/3} \left(\left(\sqrt{2}+x\right)^2\right)^{1/3}}[/latex]
[TeX]-\frac{\left(\left(\sqrt{2}+x\right)^2\right)^{5/6} \sqrt{-2+2^{2/3} \left(\left(\sqrt{2}+x\right)^2\right)^{1/3}}}{2^{1/3} \left(\sqrt{2}+x\right)}[/TeX]
La fonction h(x) - [latex]\frac{\sqrt{2}+x}{\sqrt{2}}[/latex] est toujours négative sur [latex][x;\infty ][/latex]
Le crayon devrait donc toujours pouvoir s'échapper (à moins qu'il ne soit déjà coincé dans la position de la grande diagonale)
#9 - 22-07-2012 19:11:10
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,426E+3
Crayon ssur une étagère
J'ai modifié le sujet . Il est sûrement moins attractif et plus scolaire que le précédent , c'est lui qui m'avait inspiré le problème initial .
Bon courage à ceux qui continueront à s'intéresser à l'énigme malgré tout 
Vasimolo
#10 - 23-07-2012 12:41:48
- halloduda
- Professionnel de Prise2Tete
- Enigmes résolues : 24
- Messages : 495
- Lieu: Ardèche
crayon syr une étagère
Il me semblait bien aussi...
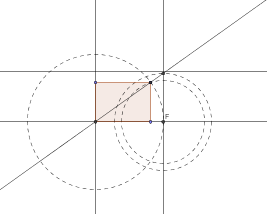
Que la forme soit un cylindre ou un dé, le centre instantané de rotation F est tel que le crayon peut sortir si et seulement si l'extrémité supérieure du crayon n'a pas à monter au début du déplacement.
La longueur du crayon doit être au moins diag.²/larg. du récipient.
#11 - 23-07-2012 22:48:51
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,426E+3
Crayon sur une étgaère
Il y a en fait deux conditions qu'il faut traiter séparément :
1°) l'ensemble cylindre plus crayon entre dans l'étagère .
2°) le crayon ne peut pas sortir sans bouger la boîte .
Vasimolo
#12 - 24-07-2012 21:14:51
- Jackv
- Elite de Prise2Tete
- Enigmes résolues : 34
- Messages : 3500
- Lieu: 94110
Crayon sur une étgère
Le problème me parait parfaitement clair :
Quand on sort le crayon, son sommet passe à une hauteur maximale quand le crayon est à 45° par rapport à l'étagère.
Conséquences :
1) On pourra toujours sortir le crayon si d >= h.
2) Si d < h, la longueur maxi est indépendante de h et fait :
(d+e) * racine(2)
Note : d peut représenter le diamètre du cylindre ou la diagonale de la base du parallélépipède.
EDIT : Au temps pour moi  . J'annule tout : j'avais raisonné sur un cas trop particulier... . J'annule tout : j'avais raisonné sur un cas trop particulier... 
#13 - 24-07-2012 22:56:11
- looozer
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 697
- Lieu: Belgique
Crayon sur nue étagère
Jackv:
Quand on sort le crayon, son sommet passe à une hauteur maximale quand le crayon est à 45° par rapport à l'étagère.
Je pense que tu te trompes ici. Prends par exemple un cylindre de diamètre et de hauteur 1 et un crayon de longueur [latex]\sqrt2[/latex] (donc déjà à 45°)
Dès que tu essaies de sortir le crayon, son extrémité supérieure monte obligatoirement.
Sur mon dessin n°2, on s'en rend compte également.
#14 - 25-07-2012 00:06:11
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,426E+3
Crayon sr une étagère
Looozer est sur la bonne piste
Il y a une solution générale ( pas complètement élémentaire ) avec quelques racines cubiques .
Penser à bien distinguer les deux cas déjà cités ( message #11 )
Vasimolo
PS : c'est une solution "maison" donc sans garantie .
#15 - 25-07-2012 01:29:43
- Franky1103
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 3221
- Lieu: Luxembourg
Crayon sur ne étagère
Bonsoir,
J'ai exprimé e en fonction de c, d et h. Je suis donc hors sujet puisqu'il faut exprimer c en fonction de d, e et h. Je vous livre quand même mes calculs qui pourraient peut-être servir, mais qui sont très indigestes.
Soient a et b les soulèvements respectifs des pointes basse et haute du crayon.
Je vais exprimer b en fonction de a, puis en trouver l'extrémum.
La partie dépassant du gobelet vaut: c-V[d²+(h-a)²],
soit: c-f(a), en posant f(a)= V[d²+(h-a)²].
Sa composante verticale vaut: v(a)=(h-a).[c-f(a)]/f(a), d’où b(a)=v(0)-v(a),
soit: b(a)=h.[c-f(0)]/f(0)+(a-h).[c-f(a)]/f(a), ou encore, avec k ne dépendant pas de a:
b(a)=k+(a-h).[c-f(a)]/f(a), d’où: b’(a)=[c-f(a)]/f(a)-(a-h).c.f’(a)/f(a)²
En posant g(a)= d²+(h-a)²=[f(a)]², on aura: f’(a)=[Vg(a)]’=0,5.g’(a)/f(a),
avec: g’(a)=2(a-h), d’où:
f’(a)=(a-h)/f(a), soit: b’(a)=[c-f(a)]/f(a)-c.(a-h)²/f(a)³=[c.f(a)²-f(a)³-c.(a-h)²]/f(a)³
Ou encore: b’(a)=[cd²-f(a)³]/f(a)³, qui s’annule pour: f(a0)³=cd²,
soit: d²+(h-a0)²=(cd²)^(2/3), soit: a0=h-[(cd²)^(2/3)-d²]^(1/2),
et on aura: f(a0)= (cd²)^(1/3)
Au final, on aura une expression d'enfer que j’ai du mal à simplifier: e > b(a0), soit:
e > h.[c-(d²+h²)^(1/2)]/[(d²+h²)^(1/2)] - {[(cd²)^(2/3)-d²]^(1/2)}.[c-(cd²)^(1/3)]/[(cd²)^(1/3)]
Bonne nuit.
#16 - 25-07-2012 18:19:23
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3802
crayon sur une étagèrz
Perso je renonce à la dérivée nulle de mon équation ( ce qui ne veut pas dire que ma dérivée ne vaut rien). C'est un chouiat lourd...
Et pis d'abord, j'ai que des stylos, na!
Et je mets pas mes stylos dans des boites cylindriques.
Et encore moins le tout sur une étagère.
#17 - 25-07-2012 18:35:03
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,426E+3
Crayon sur une étgaère
C'est bizarre , mes calculs sont plutôt simples , j'arrive à :
[latex]c\leq (e+h)\sqrt{1+\frac{d^2}{h^2^}}[/latex] pour que l'ensemble entre dans l'étagère
[latex]c>\sqrt{(\sqrt[3]{d^2}+\sqrt[3]{e^2})^3}[/latex] pour que le crayon soit bloqué .
Vasimolo
#18 - 25-07-2012 20:03:14
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,426E+3
crayon sue une étagère
La deuxième formule est assez curieuse car indépendante de [latex]h[/latex] : si je peux sortir le crayon de la boîte je pourrais le sortir de toute boîte de même diamètre !
Cette condition peut paraître curieuse si on oublie qu'elle est associée à l'entrée du bloc crayon-boîte dans l'étagère .
Vasimolo
#19 - 25-07-2012 20:33:19
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3802
crayon sur une étahère
Si c'est bon, c'est beau!
#20 - 25-07-2012 22:40:44
- looozer
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 697
- Lieu: Belgique
Crayon sur un eétagère
J'arrive aussi à une expression indépendante de h mais elle tellement laide que je ne peux la simplifier (Wolfram non plus d'ailleurs).
Je suis intéressé la logique qui aboutit à la tienne, Vasimolo.
#21 - 26-07-2012 00:43:51
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,426E+3
Crayon sur une étaagère
Il est un peu tard , mais demain je fais un effort 
Vasimolo
#22 - 26-07-2012 09:34:43
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,426E+3
#23 - 26-07-2012 13:01:10
- ThomasLRG
- Habitué de Prise2Tete
- Enigmes résolues : 41
- Messages : 31
Crayon sur une étagrèe
Bien vu Vasimolo. En effectuant les calculs différement je n'arrivais pas à trouver de formule simple 
Par contre, la fonction f n'admet pas de maximum, elle est décroissante puis croissante. D'ailleurs on intuite facilement que si on ne contraint pas un crayon à toucher le fond du pot, alors on peut ranger un crayon aussi grand qu'on veut du moment qu'il est assez penché.
En fait la fonction f est décroissante, puis croissante et admet un minimum M.
la valeur critique intervient d'après les calculs de Vasimolo pour [latex]\hat{a}= arctan(x)[/latex]. Si dans ce cas, le crayon touche le fond du pot on a [latex]h_0 = \frac {d}{tan(\hat{a})} = \frac{d}{x} = d \sqrt[3]{\frac{e}{d}}[/latex]
Ainsi, si dans la situation initiale le crayon touche le fond du pot, 2 cas se présentent :
- soit [latex]h \leq h_0[/latex], alors la taille maximale du crayon est donnée par la taille d'un crayon qui touche à la fois le fond du pot et l'étagère.
- soit [latex]h > h_0[/latex], alors la taille maximale du crayon est le M donné par Vasimolo, qui correspond à la distance minimale par lequel le crayon doit passer pour sortir du pot.
Thomas
#24 - 26-07-2012 14:29:19
- looozer
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 697
- Lieu: Belgique
Crayon sru une étagère
Efficace et beaucoup plus "simple" que prévu 
#25 - 26-07-2012 17:06:47
- Clydevil
- Expert de Prise2Tete
- Enigmes résolues : 29
- Messages : 914
- Lieu: Seahaven island
Crayon sur une éétagère

Je commercialise ce magnifique pot à crayon garanti toute étagère.
(avec lequel le problème précédent ne se pose pas)
Une révolution dans l'histoire du pot à crayon!

Mots clés des moteurs de recherche
|
 |

 Accueil
Accueil
 Forum
Forum












