quelles sont les regles de deplacement? peut-on repasser sur une arete plusieurs fois?

Je préfère raisonner en terme de probabilités uniformes, il suffit de multiplier par 3^n pour avoir le nombre de balades.

Au bout d'un nombre pair de déplacements, la fourmi est soit en A, soit en l'un des 3 sommets situés au bout d'une diagonale de face issue de A.
Soit p(2n) la probabilité que la fourmi soit en A au bout de 2n déplacements.
Pour n=0, o a p(0)=1.
J'obtiens avec un arbre de choix :
[TeX]p(2n+2)=\frac 13 p(2n)+\frac 29 (1-p(2n))[/latex] d'où [latex]p(2n+2)=\frac 29 + \frac 19 p(2n)[/TeX]
On observe alors :
[TeX]p(2n+2)- \frac 14 =\frac 19 [p(2n)- \frac 14][/TeX]
On voit apparaître une belle suite géométrique de raison 1/9 et de terme initial 3/4.
Alors :
[TeX]p(2n)=\frac 14 + \frac 34 (\frac 19)^n[/TeX]
Nombre de balades revenues en A au bout de 2n déplacements : [latex]\frac {9^n + 3}4[/latex]
Nombre de balades correspondant au cas n°3, pour chacun des 3 sommets concernés : [latex]\frac {9^n - 1}4[/latex] justifié par l'événement contraire.

Au bout d'un nombre impair de déplacements, la fourmi est soit en l'un des 3 sommets situés au bout d'une arête issue de A soit au point opposé à A dans le cube, sommet que je note G.
Soit p(2n+1) la probabilité que la fourmi soit en G au bout de 2n+1 déplacements.
Pour n=0, o a p(1)=0.
Des calculs similaires donnent :
[TeX]p(2n+3)- \frac 14 =\frac 19 [p(2n+1)- \frac 14][/TeX]
On voit apparaître une autre suite géométrique de raison 1/9 et de terme initial -1/4.
Alors :
[TeX]p(2n+1)=\frac 14 - \frac 14 (\frac 19)^n[/TeX]
Nombre de balades aboutissant en G au bout de 2n+1 déplacements : [latex]\frac {3(9^n -1)}4[/latex]
Nombre de balades correspondant au cas n°2, pour chacun des 3 sommets concernés : [latex]\frac {3 \cdot 9^n + 1}4[/latex] obtenu également par événement contraire.

J'espère que j'ai bon, sinon je réclame l'anonymat

3 bonnes réponses ! bravo à scarta, scrabblor et falcon!

Rappel, on peut se déplacer sur les arêtes uniquement, revenir sur ses pas, repartir, bref, tout ce qui compte, c'est qu'en partant de [latex]A[/latex], et en [latex]n[/latex] déplacements élémentaires, on arrive en [latex]B[/latex]. La réponse est sous la forme d'une fonction de [latex]n[/latex].

[img][/img]

La solution la plus élégante est la récurrence. J'avais aussi écris une démonstration utilisant le dénombrement, et comptant explicitement les déplacements possibles avec une méthode similaire à celle expliquée dans l'énigme "balade sur un carré", mais je'ai la flemme de la réécrire. L'idée est qu'on a une double somme de coefficients binomiaux, et que la somme à l'intérieur se transforme en la moitié de [latex]2^n[/latex] et des brouettes, et que la somme totale devient le quart de [latex]3^n[/latex] et des brouettes, qui est la solution.

Pour la résolution par récurrence, en voici une version (un peu) simplifiée, ou je détaille  beaucoup la récurrence.

Tout d'abord, étudions les symmétries du problème. Encore une fois, la parité de [latex]n[/latex] détermine les positions où l'on peut-être :
- pair, on est soit au départ (cas 1), soit dans le cas 3
- impair, on est soit dans le cas 2, soit dans le cas 4.

A partir de là, il suffit de 2 suites pour résoudre le problème, que je note [latex]u[/latex] et [latex]v[/latex], comme sur l'image :


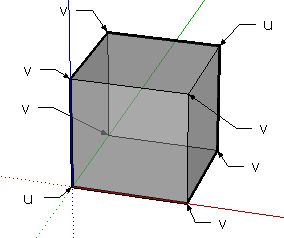
Pourquoi cela suffit-il ? Parce que la parité donne accès aux 4 cas différents !
En effet, soit on est sur un point de type [latex]u[/latex], et dans ce cas un [latex]n[/latex] pair implique qu'on est dans le cas 1, et un [latex]n[/latex] impair dans le cas 4. Soit on est sur un point de type [latex]v[/latex], et dans ce cas un [latex]n[/latex] pair implique qu'on est dans le cas 3, et un [latex]n[/latex] impair dans le cas 2.

Ensuite, la récurrence proprement dite : Etre en un point de type [latex]u[/latex], c'est venir d'un de ses trois "voisins" de type [latex]v[/latex]. Et etre en un point de type [latex]v[/latex], c'est venir soit d'un de ses deux "voisins" de type [latex]v[/latex], soit de son voisin de type [latex]u[/latex] :


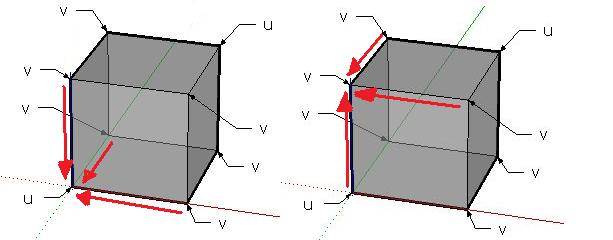
Donc la récurrence est :
[TeX]\left{\begin{array}{l} u(n+1)=3v(n) \\ v(n+1)=u(n)+2v(n)\end{array}\right.[/TeX]
La je fais place à l'élégance d'une résolution matricielle. La récurrence étant équivalente à :
[TeX]{\left( \begin{array}{c}u \\ v \end{array}\right)}_{n+1} = \left( \begin{array}{cc} 0 & 3 \\ 1 & 2 \end{array} \right) {\left( \begin{array}{c} u\\ v\end{array} \right)}_{n}[/TeX]
Pour résoudre cette récurrence, il suffit de calculer les racines du polynôme caractéristique de la matrice dans la récurrence. Donc :
[TeX]\det \left( \begin{array}{cc} -x & 3 \\ 1 & 2-x \end{array}\right)=-x(2-x)-3=x^2-2x-3[/TeX]
de racines "évidentes" 3 et -1.

Donc les solutions (pour [latex]u[/latex] et [latex]v[/latex]) sont du type [latex]a 3^n+ b (-1)^n[/latex].

Les valeurs initiales nous permettent de trouver ces coefficients :
[TeX]\left{\begin{array}{l} u(0)=a_u +b_u =1 \\ u(1) = 3a_u - b_u = 0 \\v(0)=a_v+b_v =0 \\v(1)=3a_v-b_v=1 \end{array}\right. \Rightarrow \left{\begin{array}{l} a_u=1/4 \\ b_u = 3/4 \\ a_v=1/4 \\ b_v=-1/4 \end{array} \right.[/TeX]
Et donc :
[latex]\left{ \begin{array}{l} u(n)=\frac{3^n+3(-1)^n}{4} \\ v(n)=\frac{3^n-(-1)^n}{4}\end{array}\right.[/latex].

Voili voilou !

J'ai eu du mal à comprendre l'énoncer alors les réponses O_O.

+1