Forum dédié aux énigmes et à toutes formes de jeux de logique. | Déconnexion |
|
Tu n'es pas identifié sur Prise2tete : s'identifier.  Accueil Accueil
 Forum Forum
|
 |
#1 - 01-07-2013 23:02:58
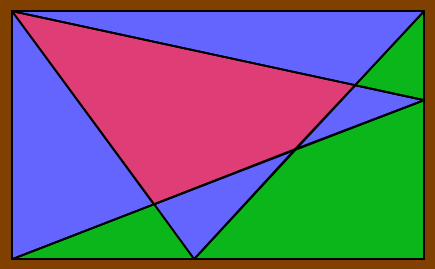
Gééométrie contemporaineBonjour à tous,
#0 Pub#2 - 01-07-2013 23:08:06
Géomértie contemporaineJ'imagine que l'aire en rouge est à l'intersection de deux triangles isocèles ? "L'expérience est une lanterne qui n'éclaire que celui qui la porte." L-F. Céline #3 - 01-07-2013 23:30:57
Gémétrie contemporaineà shadock : #4 - 01-07-2013 23:43:27
Géométrie cnotemporaineJe dirais rouge /vert = 1. Il y a sûrement plus simple. #5 - 01-07-2013 23:57:18#6 - 02-07-2013 00:02:16
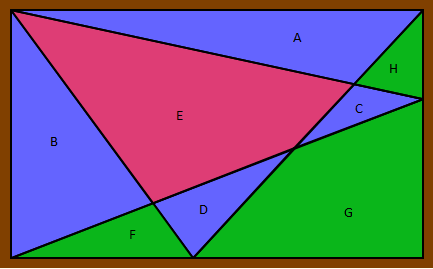
héométrie contemporaineSoient les surfaces suivantes: #7 - 02-07-2013 00:07:47#8 - 02-07-2013 00:10:27
géométrue contemporaineAlors en supposant qu'il n'y ait que des triangles isocèles puisqu'à priori ce que l'on cherche est une constance, et en utilisant la méthode bourrin du prépa fatigué qui consiste à trouver l'équation de toutes les droites afin de déterminer les coordonnées de points d'intersections des droites, puis de calculer l'aire de tout plein de petit triangle avec le produit vectoriel avec la formule suivante : "L'expérience est une lanterne qui n'éclaire que celui qui la porte." L-F. Céline #9 - 02-07-2013 00:24:31
Géométrie contempoarineTon raisonnement à partir d'un cas particulier est de bonne guerre shadock, on peut même pousser les deux sommets dans les coins du rectangle pour avoir une moitié rouge et l'autre moitié verte. #10 - 02-07-2013 00:33:09
Géométrie contepmoraineC'est à dire que j'ai une très mauvaise capacité pour imaginer les déplacements des figures dans l'espace donc j'évite, alors je fais gaffe ^^ "L'expérience est une lanterne qui n'éclaire que celui qui la porte." L-F. Céline #11 - 02-07-2013 01:30:25
Géométrie conteporaine
#12 - 02-07-2013 01:47:09#13 - 03-07-2013 11:20:58#14 - 03-07-2013 11:36:32#15 - 03-07-2013 19:35:48
géolétrie contemporainePerso les noeuds pap avec un chapeau de clown même dans un congrés d'EELV je trouve ça lourd! #16 - 03-07-2013 23:13:37
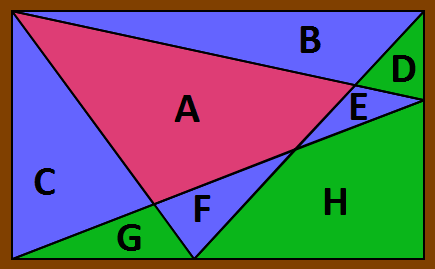
géomérrie contemporaineOn note de A et H les aires suivantes : #17 - 04-07-2013 01:17:40#18 - 04-07-2013 13:15:59
Géométtrie contemporaineJe prends comme hypothèse qu'on parle des surfaces coloriées. #19 - 04-07-2013 14:17:59
géométrie cpntemporaine
#20 - 04-07-2013 14:36:38#21 - 04-07-2013 20:19:04
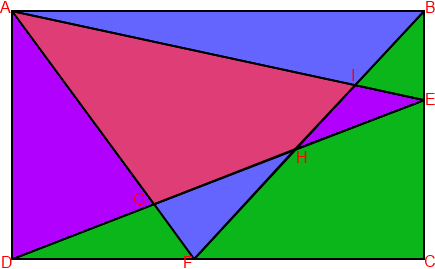
Géométrie contemporrainesuite #22 - 04-07-2013 22:47:44
Géométrie conttemporaineTout bon, fmifmi. Réponse rapideSujets similaires
Mots clés des moteurs de recherche
|
 | |||||||||||||||||||||||||||||||||||
| Prise2Tete Forum Statistiques Liste des membres Hall of Fame Contact | |||||||||||||||||||||||||||||||||||||
Un jeu où seules la réflexion, la logique et la déduction permettent de trouver la solution.