 |
#1 - 03-12-2011 23:35:05
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
gâtrau 47
Il est passé aux trapèzes et malgré tous ses efforts mon pâtissier ne parvient pas à composer un gâteau donnant des parts latérales globalement plus grosses que les parts nord-sud .

Bref peut-il trouver un trapèze tel que l'aire blanche soit supérieure à l'aire jaune ?
Comme toujours , il ne s'agît pas de sortir l'artillerie lourde mais de chercher une approche originale 
Bon courage !
Vasimolo
#2 - 04-12-2011 08:46:31
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3839
gâteai 47
Le déficit de blanc est un trapèze identique au trapèze original mais de proportion plus petite dans un rapport proportionnel au rapport grande base/petite base.
Je n'ai pas encore quantifié ce rapport...
On trace une parallèle aux bases qui passe par l'intersection des diagonales et une autre qui passe par le milieu de la hauteur, et une 3ème qui est la symétrique de la 1ère par rapport à la seconde (donc bien 3 parallèles aux bases)
On trace par ailleurs un rectangle grande base/ hauteur du trapèze.
Le déficit de blanc est la portion de ce rectangle comprise entre les 1eres et 3èmes parallèles auquel on ôte la partie comprise dans le trapèze. Cette partie résiduelle est un trapèze identique à l'original mais en modèle réduit.
Si d est le décalage de l'intersection des diagonales par rapport à la mi hauteur du trapèze, et B et b les grande et petite base, la surface de ce trapèze vaut sauf erreur:
S=d(B-b).
Comme d=(h/2)(B-b)/(B+b)
alors S vaut h(B-b)²/(2B+2b).
J'ajouterai que le rapport entre le déficit de la surface blanche et la surface du trapèze est le carré du rapport entre la différence B-b sur la somme B+b.
Autrement dit, le petit trapèze déficit est le modèle réduit de l'original dans le proportion (B-b)/(B+b).
#3 - 04-12-2011 11:50:24
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
Gâteau 74
Oui Nodgim 
Vasimolo
#4 - 04-12-2011 20:40:06
- dhrm77
- L'exilé
- Enigmes résolues : 49
- Messages : 3004
- Lieu: Fanning Island-?-Lac Tele,Mali
Gâteau 74
On peut prouver que non, temps que les faces qui sont paralleles sont horizontales, les triangles jaunes sont superieurs ou egaux aux triangles blancs.Mais je n'ai pas le temps de chercher une preuve.
(Ils sont egaux dans le cas d'un rectangle)
Great minds discuss ideas; Average minds discuss events; Small minds discuss people. -Eleanor Roosevelt
#5 - 04-12-2011 22:53:24
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
Gâteau 477
@Dan : Un parallélogramme suffira 
Vasimolo
#6 - 05-12-2011 15:25:10
- Franky1103
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 3238
- Lieu: Luxembourg
gâtzau 47
Bonjour,
Soient a et b les bases supérieure et inférieure du trapèze
Soient h1 et h2 les hauteurs des triangles inférieur et supérieur
On aura: S1=ah1/2, S2=bh2/2 et St=(a+b)(h1+h2)/4
On veut que: S1+S2<St soit 2ah1+2bh2<ah1+ah2+bh1+bh2
ou encore a(h1-h2)<b(h1-h2) avec 2 possibilités:
soit h1<h2 ce qui donne a>b, soit h1>h2 ce qui donne a<b
Or h1<h2 (resp. h1>h2) est équivalent à a<b (resp. a>b)
Comme a ne peut pas être à la fois <b et >b, on en déduit que
l'aire blanche est toujours inférieure ou égale à l'aire jaune
L'égalité des aires n'est obtenue que pour un parallélogramme (a=b)
Bonne journée.
Frank
Remarque: ma solution est HS car un peu artillerie lourde quand même
#7 - 05-12-2011 17:43:18
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
Gâteeau 47
Oui Frank c'est un peu la même idée que celle de Nodgim . C'est aussi celle que j'ai eu dans un premier temps .
J'ai trouvé une preuve du genre "sans un mot et sans calcul" .
Vasimolo
#8 - 05-12-2011 18:17:52
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3839
gâyeau 47
Par pliage j'imagine, selon une parallèle aux bases et passant par l'intersection ?
C'est en effet immédiat!
#9 - 05-12-2011 18:44:32
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 6,191E+3
Gâteu 47
En prenant des paraléllogrammes dans lesquels l'aire blanche = l'aire jaune, il reste à comparer A et B.
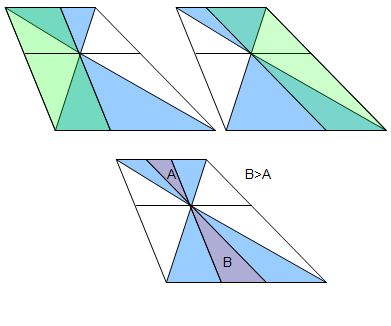
B-A est clairement positif donc l'aire jaune sera toujours plus grande.
#10 - 05-12-2011 19:09:44
- TiLapiot
- Expert de Prise2Tete
- Enigmes résolues : 16
- Messages : 852
- Lieu: au terrier ;^)
gâreau 47
Pfff, avec ce gâteau 47, tu me poses un lapin  
Comme toujours , il ne s'agît pas de sortir l'artillerie lourde mais de chercher une approche originale
Raaah mince alors, ce n'est donc pas pour le lapin 
Soit dit en passant, j'admire beaucoup les raccourcis de certaines précédentes solutions matheuses de certains, aussi expéditives que rusées.
Bon, par contre, j'M moins quand c'est si concis que cela en devient inaccessible à ma paire de neurones léporidesques 
#11 - 05-12-2011 20:10:44
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
gâtrau 47
@Nodgim : je ne comprends pas ton pliage !!!
@gwen : pas mal , ce n'est pas loin de ce que j'ai fait 
Allez TiLapiot , on creuse 
Vasimolo
#12 - 05-12-2011 22:14:50
- Franky1103
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 3238
- Lieu: Luxembourg
gâtezu 47
Re-bonjour,
Voici un nouveau raisonnement "sans calcul" et presque "sans mot"  . D'abord, je remarque que faire "glisser" la base supérieure du trapèze par rapport à la base inférieure ne change rien aux surfaces. Je place donc ces bases de façon à ce les diagonales soient perpendiculaires. Puis, je plie mon trapèze suivant une des diagonales et je m'apercois alors que ce qui reste de surface jaune sera toujours supérieur à ce qui reste de surface blanche. Il en est de même avec les surfaces de départ. . D'abord, je remarque que faire "glisser" la base supérieure du trapèze par rapport à la base inférieure ne change rien aux surfaces. Je place donc ces bases de façon à ce les diagonales soient perpendiculaires. Puis, je plie mon trapèze suivant une des diagonales et je m'apercois alors que ce qui reste de surface jaune sera toujours supérieur à ce qui reste de surface blanche. Il en est de même avec les surfaces de départ.
Bonne soirée.
Frank
#13 - 05-12-2011 23:11:53
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
Gâteu 47
Oui Frank ça marche aussi 
C'est amusant de voir le nombre d'approches différentes pour un exercice aussi élémentaire , surtout si on refuse le calcul . C'est ce qui fait la beauté de la géométrie .
Vasimolo
#14 - 06-12-2011 17:21:50
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3839
GGâteau 47
Oublie ce pliage, c'est n'importe quoi...
#15 - 06-12-2011 22:46:45
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
fâteau 47
Voilà la solution que j'avais trouvée , j'espère qu'elle peut se passer de commentaire .

J'ai tendance à préférer celles de Gwen et Frank , sans doute parce que je n'y avais pas pensé .
Merci pour la participation 
Vasimolo
Mots clés des moteurs de recherche
|
 |
|
Prise2Tete
Forum
Statistiques
Liste des membres
Hall of Fame
Contact
|

 Accueil
Accueil
 Forum
Forum









