 |
#1 - 23-07-2018 12:02:53
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
gâteai 153
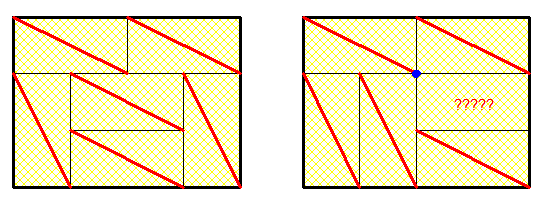
Mon pâtissier confectionne des gâteaux à base de gaufrettes 2X1 dont une diagonale est soulignée d'un trait de coulis de fraises . Il a remarqué que certaines réalisations ne permettaient pas de séparer le coulis entre deux gaufrettes :
Quelles positions des gaufrettes sont acceptables ???
La réponse n'est pas dans la taille du gâteau ni dans le nombre de gaufrettes orientées 1X2 ou 2X1 . Peut-être l'existence d'un point de contact entre quatre gaufrettes ???
Amusez-vous bien 
Vasimolo
#2 - 24-07-2018 11:31:55
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3839
Gâtea 153
Il faut construire le gâteau depuis le centre vers l'extérieur. Il faut, comme pour les murs des maisons, avoir un décalage des briques d'une rangée sur l'autre.
Le résultat est un collage de 4 pyramides à centre commun au milieu de la construction.
#3 - 24-07-2018 11:57:35
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
Gâteau 1533
Nodgim
Tu exposes différemment l'exemple que j'ai donné mais cette condition est-elle nécessaire et/ou suffisante ?????
Telle est la question 
Vasimolo
#4 - 24-07-2018 18:11:18
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3839
Gâteau 15
En fait, il faut regarder les points (extrémités des diagonales). Il n'y a qu'une seule façon de couvrir 2 points consécutifs (en fait une bonne et une mauvaise qui conduit dans une impasse). Dans ton dessin de droite, tu n'as pas couvert en priorité les 2 points consécutifs en bas. Si tu le fais, tu vas créer un nouveau 2 pts consécutifs dont le recouvrement est incompatible avec ta brique horizontale sous " ???? ".
Par ailleurs, ton dessin de droite t'amène à placer 3 points consécutifs, ce qui est impossible à couvrir.
Et puis, en construction d'un rectangle, il vaut mieux ne pas avoir à boucher des trous. Car quand un rectangle est formé, on peut toujours le démonter sans avoir à en faire.
#5 - 25-07-2018 12:21:31
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
Gâteau 15
On a bien compris que dès qu'on avait choisi une diagonale les jeux étaient faits avec ou sans succès selon la configuration . Il y a plusieurs points qu'il faudrait éclaircir en oubliant l'illustration dont j'ai précisé le rôle .
1°) En cas de réalisation possible , les pentes des diagonales ont-elles forcément toutes le même signe et pourquoi ?
2°) Si on change toutes les diagonales transforme-t-on une solution en une autre ?
3°) En cas d'impossibilité pourquoi existe-t-il toujours un point de contact entre quatre gaufrettes ?
4°) Pourquoi y'a-t-il forcément une solution quand quatre gaufrettes ne partagent jamais le même sommet ?
Je sais , ça fait beaucoup de questions ( qui ne sont pas indépendantes ) 
Vasimolo
#6 - 25-07-2018 12:32:47
- kryptos.fr
- Professionnel de Prise2Tete
- Enigmes résolues : 6
- Messages : 119
gâteai 153
bonjour, peut être je me trompe , je propose 2x0.5 d une grande en vertical.
www.kryptos.fr
#7 - 25-07-2018 17:19:40
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
Gâteau 15
Le but est de décrire l'ensemble des configurations pour lesquelles c'est possible 
Vasimolo
#8 - 26-07-2018 09:30:10
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3839
Gâtau 153
J'en reste à mon idée, que je précise.
On construit le gâteau dans les coordonnées entières d'un repère orthonormé. On peut modéliser une face du gâteau par 0 si absence de diagonale et 1 sinon.
L'idéal est d'avoir une alternance parfaite de 0 et de 1, mais ce n'est pas possible.
Il est évident qu'on ne peut pas ajouter une couche à une face 111...c'est à dire avec trois 1 consécutifs.
Ce l'est moins, mais on ne peut pas non plus ajouter une couche à une face comportant ...11...qui n'est pas en extrémité, même si 11 est précédé d'un seul 0.
A partir de là, il faut éviter de poser des briques qui amèneraient à se trouver dans la situation ci-dessus. Ou alors admettre qu'on abandonne 1 face (mais dans ce cas on doit aussi abandonner l'autre face) et ne déployer que dans une seule dimension.
#9 - 26-07-2018 10:34:12
- kryptos.fr
- Professionnel de Prise2Tete
- Enigmes résolues : 6
- Messages : 119
âteau 153
Ce que je vois c est une rotation, les vertical devienne les horizontal et les horizontal devienne les vertical vers la gauche.
www.kryptos.fr
#10 - 26-07-2018 11:35:23
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
gâtzau 153
@Nodgim : il y a bien une façon de coder les sommets avec des 0 et des 1 mais je n'ai pas réussi à le faire proprement sans dissocier les cas .
@Kryptos : je ne suis pas sûr que tu aies compris la question 
Vasimolo
PS : je n'ajoute pas de temps , le problème ne passionnant vraiment pas les foules .
#11 - 26-07-2018 12:04:07
- Franky1103
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 3238
- Lieu: Luxembourg
gâtzau 153
Comme souvent, le nombre de posts ne reflète pas l'intérêt pour une énigme. Personnellement je suis intrigué par ce problème, mais comme je ne trouve rien de bien probant, je n'ai rien posté.
#12 - 26-07-2018 12:23:32
- kryptos.fr
- Professionnel de Prise2Tete
- Enigmes résolues : 6
- Messages : 119
Gâteau 53
il faut faire quoi? avec des chiffre j ai pas trop compris.
Si 0 est le départ et 1 l arriver es qu' il faut faire les diagonales qui sont en prolongement.
1001
www.kryptos.fr
#13 - 26-07-2018 12:31:37
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
gâreau 153
Je laisse donc le problème ouvert .
La réponse au problème est bien celle pressentie mais j'aimerais bien voir des solutions autres que la mienne 
Vasimolo
PS : c'est un problème original ( vu nul part ailleurs  ) )
#14 - 26-07-2018 12:33:52
- kryptos.fr
- Professionnel de Prise2Tete
- Enigmes résolues : 6
- Messages : 119
Gâteau 1533
si il faut avec 2 et 1pour moi donne ça :
2121 ou 2112
ci c est pas ça je laisse tomber.
www.kryptos.fr
#15 - 26-07-2018 12:39:54
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
GGâteau 153
@Kryptos : je crois que tu n'as vraiment pas compris le problème 
Essaie peut-être de voir ailleurs 
Vasimolo
#16 - 26-07-2018 12:40:34
- kryptos.fr
- Professionnel de Prise2Tete
- Enigmes résolues : 6
- Messages : 119
#17 - 26-07-2018 13:26:00
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3839
Gteau 153
Vasimolo a écrit:@Nodgim : il y a bien une façon de coder les sommets avec des 0 et des 1 mais je n'ai pas réussi à le faire proprement sans dissocier les cas .
On ne va pourtant pas loin du tout....
Soit la face 011010101.....à compléter par le dessus
1ere option: une brique verticale, suivie obligatoirement d'une horizontale.
01
0100
1111010101
extrait :
01
010
On ne peut pas compléter le coude autrement que une verticale.
..10
010
0110
extrait :
..10
010
Cet extrait est le symétrique du précédent, même remède, même décalage résiduel.
2ème option :
1 brique horizontale suivie obligatoirement d'une verticale :
Même scénario que ci-dessus.
#18 - 26-07-2018 18:58:49
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
Gâtaeu 153
On voit assez bien que ça marche quand chaque sommet ( sauf les quatre coins ) appartiennt à deux gaufrettes exactement et on peut formaliser ça simplement en associant 0 à chaque sommet en bas à gauche d'une gaufrette et 1 à chaque sommet en haut à droite ( il n'y a pas de double numérotation possible ) . Le problème est dans la réciproque : pourquoi une position dont l'un des sommets appartient à quatre gaufrettes ne pourra jamais convenir ????
On peut bien sûr répondre qu'en partant d'un point critique on ne pourra jamais compléter le rectangle avec des 0 et des 1 comme dans le sens direct , mais il faudrait une preuve un peu plus élaborée . En bref éviter les on voit très bien que , sinon l'ensemble de l'énigme peut se résumer à ce : "on voit très bien que ..." 
Vasimolo
#19 - 27-07-2018 08:16:06
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3839
Gâtaeu 153
Je ne sais pas trop où tu veux en venir avec le critère " point de contact avec 4 briques " : On peut très bien empêcher le placement d'une brique dans un angle avec seulement 2 briques dans cet angle, et à contrario, on peut très bien placer une 4ème brique dans un angle entouré de 3 briques.
#20 - 27-07-2018 10:09:02
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
Gâteau 53
En fait je crois qu'on est en train de dire pratiquement la même chose mais sous un angle différent : je résume en précisant le vocabulaire .
Les nœuds du gâteau sont les sommets des gaufrettes , il y a trois types de nœuds :
Ceux qui sont les sommets d'une seule gaufrette ( ce sont les sommets du gâteau ) , ceux qui sont les sommets de deux gaufrettes et ceux qui sont les sommets de quatre gaufrettes .
On a montré clairement que s'il n'y avait que des nœuds des deux premières catégories , le gâteau était réalisable . Il reste à trancher le cas ou le gâteau aurait des nœuds partagés par quatre gaufrettes ( le deuxième dessin du message initial ) .
On peut raisonner par l'absurde et supposer qu'on peut réaliser un gâteau avec de tels nœuds . Sur les quatre gaufrettes partageant l'un de ces nœuds , il y a au moins deux voisines ( partageant un peu plus qu'un sommet ) dont la bonne diagonale ne passe pas par ce nœud . Aux symétries près , on a trois possibilités :
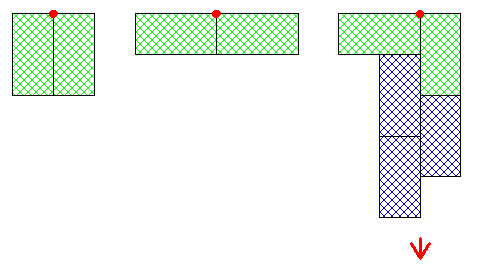
La contradiction est immédiate dans les deux premiers cas . Pour le troisième on génère une suite infinie de gaufrettes qui n'entre clairement pas dans le cadre de la réalisation .
C'est ma façon de voir , il y a certainement plein d'autres approches 
Vasimolo
#21 - 27-07-2018 10:33:40
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3839
Gâteau 135
Malheureusement, il existe au moins 1 cas " noeud à 2 sommets " qui coince :
Empile 2 gaufrettes diagonales pentes + (dans le sens algébrique habituel), et une troisième par dessus, décalée d'une unité vers la droite, de pente négative: il est impossible de placer une gaufrette dans l'angle rentrant.
#22 - 27-07-2018 10:37:34
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
GGâteau 153
Désolé , je ne comprends pas , tu pourrais donner les coordonnées des sommets des gaufrettes fautives ?
Vasimolo
#23 - 27-07-2018 11:45:36
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3839
Gâteau 15
Oui, je donne même un montage 5 gaufrettes, où il ne reste plus qu'à placer la 6ème pour faire un rectangle :
(00,12) (10,31) (11,32) ( 03,22) (23,42)
#24 - 27-07-2018 11:58:44
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
gâteay 153
Oui ben c'est possible en traçant toutes les diagonales montantes ou descendantes selon ses préférences 
Vasimolo
#25 - 27-07-2018 12:44:42
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3839
Gâteau 513
L'énoncé ne l'interdit pas.
Avant d'avancer la règle des 4 sommets, il faudrait prouver celle de la pente unique.
Sinon, ton énoncé n'indique pas la forme des gâteaux, il faudrait préciser qu'ils doivent être rectangulaires.
|
 |

 Accueil
Accueil
 Forum
Forum









