|
#1 - 10-07-2015 00:24:31
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
#2 - 10-07-2015 10:50:25
- enigmatus
- Expert de Prise2Tete
- Enigmes résolues : 0
- Messages : 561
gâtzau 101
Bonjour,
En passant en revue tous les cas possibles, je trouve une probabilité de 1 pour N=2, et de 2/3 pour N=4,6,8,10.
Je ne sais pas l'expliquer.
#3 - 10-07-2015 16:53:44
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
Gâteeau 101
C'est la bonne réponse Enigmatus 
Un résultat aussi élémentaire doit pouvoir se justifier simplement 
Vasimolo
#4 - 11-07-2015 23:12:50
- kossi_tg
- Professionnel de Prise2Tete
- Enigmes résolues : 18
- Messages : 307
- Lieu: Montargis
Gâteau 1011
Pour N parfums différents et donc 2*N blocs carrés, la probabilité cherchée est de 1/N.
Dans le cas présent, N=50 (100 blocs carrés) donc la probabilité cherchée est 1/50=0.02
Entrain de chercher une démo assez simple 
#5 - 12-07-2015 12:28:02
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
âGteau 101
Non Kossi , la probabilité est bien plus grande 
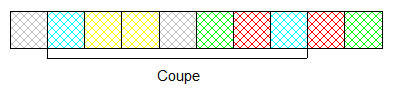
Je précise que si la disposition des blocs est faite au hasard , j'ai toute liberté pour le choix de la couleur définissant ma part ( désignée par le mot coupe sur le dessin ) .
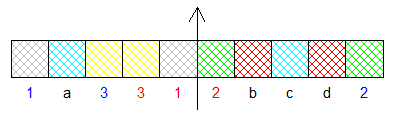
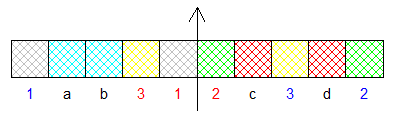
Une question très bête , si on a en plus le choix entre la partie centrale ou les chutes gauches et droites réunies ( en gardant les blocs de la couleur choisie ) : quelle est la probabilité de récupérer au moins un bloc de chaque couleur ?
Vasimolo
#6 - 13-07-2015 07:53:49
- enigmatus
- Expert de Prise2Tete
- Enigmes résolues : 0
- Messages : 561
Gâteau 1001
Pour la "question très bête" en #5, en s'imposant de choisir uniquement la partie gauche, je trouve (au moins pour N=2,4,6,8,10,12) une probabilité de 100 % d'avoir au moins un bloc de chaque couleur (idem en choisissant la partie droite).
#7 - 13-07-2015 09:15:41
- Franky1103
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 3238
- Lieu: Luxembourg
âteau 101
Expérimentalement avec un tableur je trouvais aussi 2/3, mais j'étais également incapable de l'expliquer (avec en sus un doute sur ce résultat): à partir de 10, ça commence à être fastidieux. Et j'ai pensé à une récurrence (démo non finalisée).
#8 - 13-07-2015 11:58:54
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
Gâteau 10
La réponse au problème initial est bien 2/3 pour un nombre quelconque de paires de parts .
Il y a une démonstration assez simple et non calculatoire que je vous laisse chercher encore un petit peu .
Pour la variante c'est encore plus bête 
On imagine que le gâteau se referme pour former un cercle :
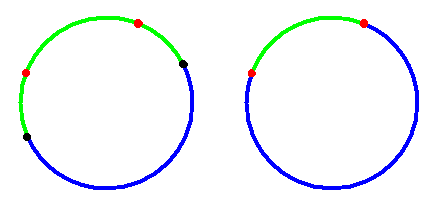
Et on choisit deux parts ( en noir sur le premier cercle ) pour que l'arc bleu contienne le maximum de parfums différents . Si par hasard un parfum manquait à l'arc bleu , il existerait deux points du même parfum ( rouge ) dans l'arc vert et il suffirait de prolonger l'arc bleu jusqu'à ces deux points pour contredire la définition de l'arc bleu . Donc l'arc bleu contient tous les parfums . Il reste à redévelopper le gâteau et selon que la cassure se situe dans la partie verte ou bleue , la partie centrale ou la partie gauche+droite va contenir l'ensemble des parfums .
Merci aux participants .
Vasimolo
#9 - 15-07-2015 06:50:04
- enigmatus
- Expert de Prise2Tete
- Enigmes résolues : 0
- Messages : 561
Gâtea u101
Il semble que l'on puisse réussir à tous les coups si l'on s'impose de prendre la portion de gauche.
Je choisis 2 parts de couleurs identiques, et je me positionne sur celle de gauche :
- soit toutes les couleurs apparaissent parmi la part choisie et celles qui sont à sa gauche, et c'est bon.
- soit il existe, à droite de la part choisie, une paire de parts d'une couleur non encore représentée. Je me positionne alors sur celle de gauche.
Et je recommence le raisonnement.
Il va sans dire que le résultat est le même si l'on s'impose de prendre la portion de droite.
#10 - 15-07-2015 08:26:32
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
âGteau 101
Il me semble qu'avec un gâteau de type JBJBRR on ne puisse pas récupérer tous les parfums en prenant une part à gauche ou au centre , non ?
Vasimolo
#11 - 15-07-2015 09:10:05
- enigmatus
- Expert de Prise2Tete
- Enigmes résolues : 0
- Messages : 561
Gâtau 101
Vasimolo #10 a écrit:Il me semble qu'avec un gâteau de type JBJBRR on ne puisse pas récupérer tous les parfums en prenant une part à gauche ou au centre , non ?
Si on choisit R (JBJBRR) :
Gauche = JBJBR => C'est bon
Centre = RR
Droite = R
Si on choisit J (JBJBRR) :
Gauche = J
Centre = JBJ
Droite = JBRR => C'est bon
#12 - 15-07-2015 10:32:39
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
Gâteau 110
D'accord , je n'avais pas vu ça comme ça 
En fait la stratégie à adopter si on décide de conserver la partie gauche est de choisir la paire dont l'élément à gauche est le plus à droite possible et ça fonctionne de façon évidente .
Reste le problème initial 
Vasimolo
#13 - 15-07-2015 18:53:17
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3839
Gâtea u101
On part par exemple de l'extrême gauche:
A........A........est NOK
On recherche à l'intérieur de l'intervalle AA s'il existe un autre couple(tjs à partir de la gauche)
A...B.....B....A......
On recherche à l'intérieur de l'intervalle BB si un autre couple existe, et si oui, on continue jusqu'à refus.
Soit KK ce couple. Si Z est la couleur à l'extrême droite, le triplet ordonné KKZ a 2 solutions gagnantes et une solution perdante.
Si A.....A....est OK, alors AAZ (couleur extrême droite) est ce triplet.
#14 - 15-07-2015 19:06:05
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
#15 - 15-07-2015 19:39:44
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3839
Gâtau 101
Les lettres sont les couleurs. Z est, comme écrit, à l'extrême droite.
#16 - 15-07-2015 19:55:31
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3839
Gâteua 101
Bon, ça reste à peaufiner pour les config avec plusieurs intervalles gagnants: il faut trouver des triplets indépendants.
#17 - 16-07-2015 00:05:45
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
Gâetau 101
Je te laisse continuer sur cette voie , j'étais parti du centre mais à chacun son feeling 
Vasimolo
#18 - 17-07-2015 07:04:58
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3839
Gtâeau 101
On recherche le 1er couple A dont la 2ème couleur (à partir de la G) est la plus proche de la gauche. On fait pareil à partir de la droite (couple B). Les 2 configs possibles sont:
(...A1......A2....B2....B1..) ou (..A1.......B2....A2.....B1...)
de sorte qu'il n'y a pas de couple entre un bord et A ou B le plus proche.
On recherche s'il existe un couple C qui enjambe A et B. S'il y en a plusieurs, on choisit pour C le plus enjambant (CD........DC), mais s'ils sont imbriqués (CD.........CD), le choix importe peu, on peut arbitrairement prendre pour C le couple le plus à G.
On définit maintenant un triplet ordonné formé d'un couple et d'un isolé. Les 3 permutations possibles donneront 2 solutions gagnantes et 1 solution perdante.
-Si C n'existe pas: (A1A2B1)
-Si C existe: C1C2B1.
Ainsi, toutes les configurations possibles sont classées en 3 groupes distincts dont 2 contiennent ttes les solutions gagnantes et l'autre ttes les solutions perdantes. Il y a donc 2/3 de solutions gagnantes.
#19 - 17-07-2015 10:31:23
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
Gâteauu 101
On recherche le 1er couple A dont la 2ème couleur (à partir de la G) est la plus proche de la gauche. On fait pareil à partir de la droite (couple B). Les 2 configs possibles sont:
(...A1......A2....B2....B1..) ou (..A1.......B2....A2.....B1...)
de sorte qu'il n'y a pas de couple entre un bord et A ou B le plus proche.
On recherche s'il existe un couple C qui enjambe A et B. S'il y en a plusieurs, on choisit pour C le plus enjambant (CD........DC), mais s'ils sont imbriqués (CD.........CD), le choix importe peu, on peut arbitrairement prendre pour C le couple le plus à G.
Jusqu'ici ça va 
On définit maintenant un triplet ordonné formé d'un couple et d'un isolé. Les 3 permutations possibles donneront 2 solutions gagnantes et 1 solution perdante.
-Si C n'existe pas: (A1A2B1)
-Si C existe: C1C2B1.
Ainsi, toutes les configurations possibles sont classées en 3 groupes distincts dont 2 contiennent ttes les solutions gagnantes et l'autre ttes les solutions perdantes. Il y a donc 2/3 de solutions gagnantes.
La je ne comprends plus 
Vasimolo
#20 - 19-07-2015 10:51:15
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
|
 |

 Accueil
Accueil
 Forum
Forum