Prenons 2 myrtilles A et B, reliées (donc plus proches voisines l'une de l'autre).
Il n'y a donc aucune myrtilles dans les 2 disques de centre A (resp B) et de rayon AB et de centre A. Nous appelerons C et D les points d'intersections des 2 cercles.
Il est clair (formule à employer quand on ne veut pas faire une démo alambiqué d'un résultat qui saute aux yeux sur un dessin)... Il est clair donc que tout segment formé de 2 points en dehors des 2 disques qui coupe le segment AB a une longueur supérieur à la longueur CD = rac(3).
Donc il n'y a jamais 2 traits de coulis qui se croisent.

Supposons qu'il existe une intersection et intéressons-nous uniquement aux 4 points qui sont les extrémités des segments qui se croisent.

Nommons les points ainsi :


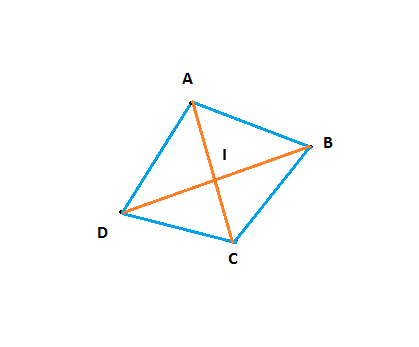
D'après le théorème du chemin le plus court de la géométrie euclidienne, on obtient les inégalités suivantes :
BC<CI+IB
AB<AI+IB
AD<AI+ID
CD<DI+IC

En additionnant les 4 inégalités on obtient :
BC+AB+AD+CD<2AC+2BD

Maintenant d'après l'énoncé, pour que A soit relié à C et que B soit relié à D, la figure doit vérifier les inégalités suivantes :
AC<AD
AC<AB
BD<BC
BD<CD

En additionnant les 4 inégalités on obtient :
2AC+2BD<BC+AB+AD+CD

On a là une contradiction qui rend impossible que deux lignes rouges se croisent.

Soit un quadrilatère ABCD et ses diagonales AC et BD. Pour joindre AB, on peut passer par la diagonale AC jusqu'à l'intersection, puis prendre l'autre diagonale. Il est évident que le segment AB est plus court que la trajectoire par les demi diagonales. Raisonnement idem pour joindre CD, qui se fait sur les 2 autres demi diagonales. Du coup, il est évident que AB+CD <AC+BD.

1er cas, réseau non connexe, seule les diagonales existent:
L'existence des segments implique que pour l'un au moins des 2 pts reliés, cette liaison est unique. On suppose alors que A et D sont ceux là.   

Si AB<AC alors on s'est trompé en choisissant AC, car B est plus proche de A que C.
Si AB>AC alors CD<BD donc on s'est trompé en choisissant BD, car C est plus proche de D que B.
Dans tous les cas, on s'est trompé avec le croisement .
Le même raisonnement s'applique si on choisit comme pts isolés les autres couples.


2ème cas, réseau connexe, 3 segments relient les 4 points, avec un croisement, par exemple CA, AB, BD. C et D sont donc les pts isolés.
Alors la liaison connexe CB, BA, AD est plus courte car elle évite les détours par l'intersection des diagonales.

@Nodgim : il me semble que tu n'as pas remarqué une chose . On peut très bien avoir tracé le segment [AB] alors que le point le plus proche de A n'est pas B .

Vasimolo

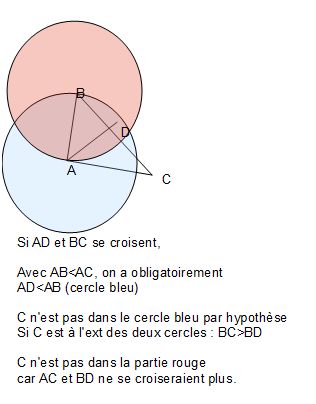
Ah si C est sur le cercle bleu, il est dans la partie violette et CD <CB ou ça ne se croise plus non plus.

Comprends pas. As tu lu à fond ma démo ? car j'ai bien prévu le cas AB>AC

D'accord mais en dessous j'écris:
"Si AB>AC alors CD<BD donc on s'est trompé en choisissant BD, car C est plus proche de D que B"
Ce qui à nouveau supprime le croisement.

Ben non, ce 2ème cas évoqué est justement le cas de C qui est le plus proche voisin de A. Cette diagonale AC est effectivement plus courte que AB, mais dans ce cas l'autre diagonale BD est forcément plus longue que la non diagonale CD.

En fait, les 2 diagonales ne peuvent être  toutes les deux en même temps les distances les plus courtes depuis les points A et D vers les points B et C.

Soit deux myrtilles M1 et M2 distantes de R.
Pour qu'il y est croisement, il faut couper le segment M1,M2 sans deposer de baies dans les cercles. Or la distance pour y parvenir est au minimum de R*rac(3)



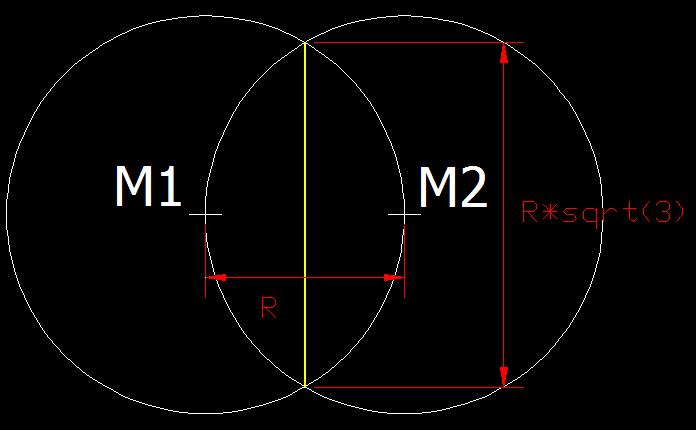
PS:
La myrtille n'est pas une graine mais l'organe végétal protégeant les graines qui s'y trouvent.

Maintenant que les réponses sont visibles par tous j'aimerais bien qu'on précise les démonstrations avec les deux disques et la racine de trois .

Je dois admettre que je fais un blocage et seule la démonstration de Nicolas ( que j'avais aussi ) m'a convaincu pour le moment .

Vasimolo

Le problème est que tu laisses des blancs énormes dans tes explications et les combler c'est résoudre l'énigme à ta place .

La somme de deux côtés opposés d'un quadrilatère convexe est inférieure à la somme des diagonales ; c'est tout à fait convaincant :

nodgim a écrit:

Si AB<AC alors on s'est trompé en choisissant AC, car B est plus proche de A que C.

Pour moi c'est faux sans autre élément d'explication

Ajouter d'autres cas non explicités à chaque nouvelle question ne clarifie rien , au contraire . Tu donnes un schéma détaillé de ta logique ou tu reconnais  que ta démo n'est pas complète .

Vasimolo

Ah bon !!!!!!!!!

Vasimolo