Le motif est un segment .

La question : On peut quadriller la galette sans traverser le segment , peut-on quadriller la même galette avec le même maillage si le segment initial est découpé en plusieurs morceaux ?

La bûche c'est pour noël 2014

Vasimolo

Si on prend un des morceaux et qu'on mette la maille de telle façon que ce morceau commence une diagonale de la maille...

Le problème est équivalent à celui qui consiste à ramener le point de départ de chaque morceau dans cette maille. (décalage oblige)

Si un morceau dépasse vers le haut ou la droite, je le redécale et je tombe sur une superposition des segments en abscisse ou en ordonnée , soit moins que la taille de la maille.

On ramène donc le problème sur une seule maille.


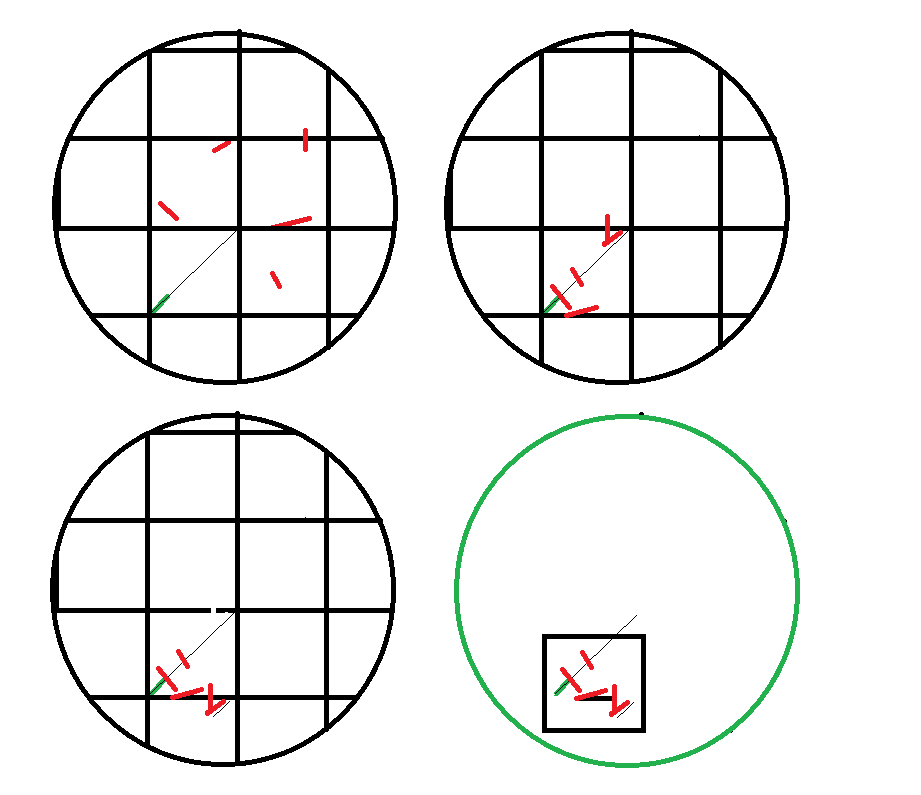
Je reporte cette maille bien placée et je remets les morceaux à leur place... Ca semble marcher toujours.

Reste à prouver que les morceaux à "une maille près" sont tous dans un secteur inférieur à la maille.

Je n'ai pas d'idée formelle de preuve, je postais juste une conviction logique mais assez difficile à mettre en mots pour moi.

Mais bon la superposition des morceaux de segment ne peut pas être plus grande que le segment initial vu qu'elle se fait en abscisce et en ordonnée avec superposition  éventuelle des coordonnées.

@shadock : le quadrillage est à mailles carrées et identique sur les deux galettes . Le dessin est une illustration , le nombre de lignes et de colonnes n'est pas limité à 3 . Le motif est découpé en un nombre fini de parties , il n'y a pas de morceaux de taille infinitésimale .

Vasimolo

J'ai, et ça ressemble beaucoup à ce qu'a entrepris Gwen.
D'abord, il existe une orientation de grille telle que la projection, sur chacun des cotés de grille, de l'ensemble des éléments, est en cumulé de longueur inférieure à la longueur d'une maille, puisque il en est de même pour  l'élément initial.
Partant de là, on peut trouver, selon cette orientation, une solution.
On peut ramener les segments autour d'une seule maille, on fait du modulo abscisse et du modulo ordonnée.
Selon l'axe des abscisses, on peut translater la grille de sorte qu'on échappe aux segments, puisque la somme des longueurs projetées sur cet axe est inférieure à la longueur d'une maille. Quand on a trouvé une solution, on cherche le réglage des ordonnées qu'on arrivera à obtenir pour la même raison.

Tu cales les traits verticaux (à écart constant ) dans un premier temps : il y a un intervalle libre au moins.

Puis tu n'y touche plus.

Tu cales alors les traits horizontaux en cherchant un intervalle libre. Ca ne change pas les premier réglage.

C'est juste le fait de trouver l'orientation de la maille qui me chiffonnait dans mon raisonnement.

1°) Pourquoi est-on assuré de pouvoir positionner une graduation sur des segments dont la longueur totale est inférieure à 1 sans qu'aucun entier ne soit sur un des segments ?

Racine de 2, pas 1 ... D'où le problème de l'orientation de la maille.

2°) Il est clair que la longueur totale de la projection sur chaque axe de coordonnées est inférieure à 2 mais pourquoi chacune d'entre elles devrait être inférieure à 1 pour une orientation donnée ?

Euh.... toujours racine de 2 non ? Pas 2.

Nodgim , d'accord pour le premier point

Pour le deuxième et je parle aussi pour Gwen : si on projette un segment de longueur [latex]\sqrt{2}[/latex] sur deux axes perpendiculaires on obtient des segments dont la longueur totale est inférieure à 2 . Cela reste vrai si on découpe le segment en plusieurs morceaux . Mais une somme inférieure à 2 sur l'ensemble des deux axes n'entraîne pas à priori que chacune des composantes soit inférieure à 1 .

Vasimolo

Ce que je voulais dire c'est qu'il y a une façon simple de justifier ce fait .

En faisant tourner continûment le quadrillage d'un quart de tour autour d'un de ses points , on change |x|-|y| en |y|-|x| donc la différence va s'annuler à un moment donné .

Vasimolo