Enigme Gâteau 81 @ Prise2Tete

Vasimolo · #1

Bonjour à tous

Tous ceux qui ont suivi du coin de l’œil les aventures de mon pâtissier savent qu'il adore transformer sa boutique en cirque où les maths ont souvent leur mot à dire . Nous sommes un peu fâchés depuis quelques temps mais je ne peux pas m’empêcher de regarder ce qu'il fabrique , surtout quand il y a foule devant sa porte , ce qui est plutôt le cas en ce moment .

Voilà ce que j'ai cru comprendre de son animation et de sa stratégie .

Il exhibe un exemple de gâteau à six côtés dont tous les angles sont égaux :

Il présente ensuite un lot de 9 bâtons :

Il propose alors au client ( ristourne à l'appui ) de l’empêcher de réaliser un tel gâteau . Celui-ci va devoir retirer un bâton , le pâtissier un autre avant qu'il ne retire le dernier bâton . Le pâtissier doit alors réaliser son gâteau avec les bâtons restants .

La stratégie du pâtissier est très simple , il retire toujours le bâton 9 sauf s'il est déjà pris , il retire alors le 1 .

On suppose que le client qui vient pour un gâteau se fiche un peu de l'affaire et qu'il choisit les bâtons complètement au hasard . Quelle est la probabilité que le pâtissier gagne avec cette stratégie ?

Est-elle perfectible ?

Amusez-vous bien

Vasimolo

PS : j'ai actualisé l'illustration du gâteau 81 qui avait été écrasé par une autre image .

Klimrod · #2

Salut,

Puisque personne ne veut répondre et que j'aime bien les gâteaux, je tente la première question.

Proba(1-9-5) = 1/9 x 1 x 1/7
Proba(5-9-1) = 1/9 x 1 x 1/7
Proba(9-1-5) = 1/9 x 1 x 1/7

Conclusion : Proba cherchée = 3 x 1/9 x 1/7 = 1/21
Donc une chance sur 21 que le pâtissier puisse fabriquer son gâteau.

J'espère que j'ai bien compris la question, car ça me paraît trop facile...
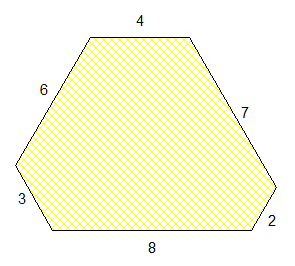
Peut-être qu'un tel gâteau à 6 côtés de longueur entière n'existe pas ?

Quant à l'optimisation, c'est une autre paire de manche et je ne vois pas comment améliorer. Je vais y réfléchir mais pour l'instant j'ai la bouche pleine .
Klim.

golgot59 · #3

Sympa ce nouveau gâteau !

Je trouve que le cuistot gagne 22 fois sur 28...

Pour commencer, voici le schéma que j'ai fait :

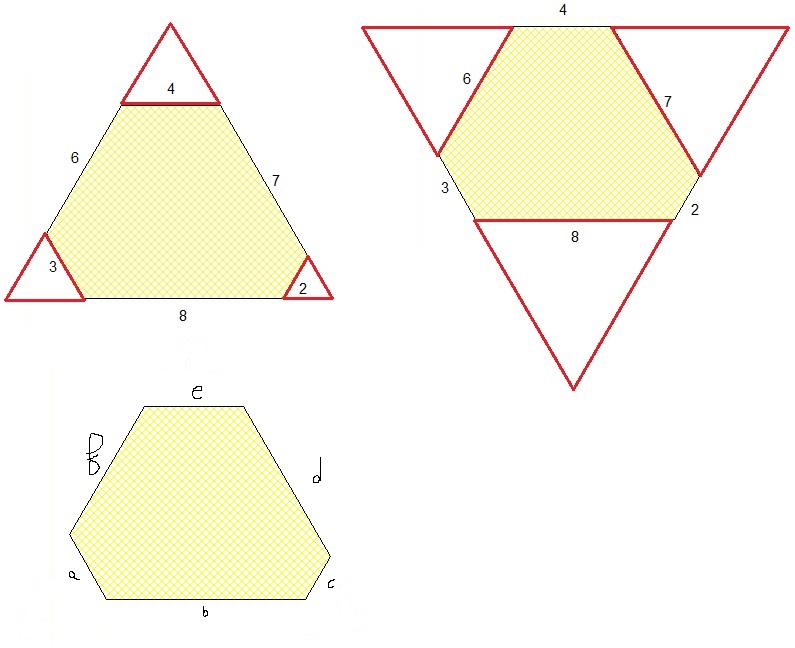
Sur les deux du haut, j'ai recopié ton exemple et montré que puisque les angles sont les mêmes dans l'hexagone, alors on peut reconstituer un triangle équilatéral en ajoutant 3 triangles équilatéraux dans 3 angles non consécutifs (2 possibilités).

En écrivant les égalités sur les longueurs des côtés de la figure du bas on tire :
a+b+c=c+d+e=e+f+a sur l'équivalent du premier triangle et
b+c+d=d+e+f=f+a+b sur le second.

et en soustrayant les 2 lignes :
a-d=c-f=e-b

Puisque le cuistot enlève toujours le segment 9 s'il reste présent à son tour, on peut considérer que le client choisit 2 segments parmi ceux de 1 à 8.

En faisant la liste des possibilités exhaustive en conservant la différence constante parmi les 3 couples de 2 côtés opposés, j'obtiens :

Différence de 1 :
8-7 6-5 4-3
87 65 32
87 65 21
87 54 32
87 54 21
87 43 21
76 54 32
76 54 21
76 43 21
65 43 21

Différence de 2 :
86 75 42
86 75 31
86 53 42
86 42 31
75 64 31
75 42 31

Différence de 3 :
85 74 63 (déjà vu)
85 63 41
74 63 52 (déjà vu)
63 52 41 (déjà vu)

Différence de 4 :
84 73 62
84 73 51
84 62 51
73 62 51

Différence de 5 :
83 72 61

Ce qui nous fait 22 possibilités différentes sur C(8,6)=28

Donc il gagne 11 fois sur 14... Pas si mal !

Quant à l'optimisation, je m'y mets !

Vasimolo · #4

Merci Klim et Golgot pour la participation

@Klim : C'est super gentil de relancer , mais en effet ce n'est pas si simple

@Golgot : Nous avons la même approche

Vasimolo

Franky1103 · #5

J'ai recensé 53 gâteaux hexagonaux possibles, en enlevant les configurations qui sont équivalentes par rotation ou par symétrie:
- le 1 et le 9 y apparaissent 28 fois chacun,
- le 2, le 5 et le 8 y apparaissent 36 fois chacun,
- le 3 et le 7 y apparaissent 37 fois chacun,
- le 4 et le 6 y apparaissent 40 fois chacun.
Le pâtissier aura donc intérêt à retirer les bâtons les moins "rentables", à savoir le 1 ou le 9 justement.
Je vérifierai demain si le fait que le client enlève un premier bâton change cet ordre du nombre d'apparitions, ce qui n'est pas évident.
Affaire à suivre ...

golgot59 · #6

Bon, c'est un peu laborieux, mais si ça t'intéresse, je trouve en appliquant à peu près la même méthode que la stratégie de ton pâtissier est perfectible :

Il faut choisir :
Choix du client -> Choix du pâtissier
1->2 ou 9
2->1
3->7
4->1, 5 ou 9
5->1, 4, 6 ou 4
6->1, 5 ou 9
7->3
8->9
9->1 ou 8

Je vais voir si je peux calculer le pourcentage de gain obtenu...

Vasimolo · #7

@Golgot ; j'ai la même stratégie que toi mais je n'ai pas les mêmes résultats dans les deux cas .
@Franky : je n'ai trouvé que 49 gâteaux mais j'ai pu en oublier .

Vasimolo

titoufred · #8

Je note a, c', b, a', c, b' les longueurs des 6 côtés de l'hexagone dans l'ordre des segments.
Par commodité les noms des côtés seront confondus avec les noms des longueurs des côtés.
L'hexagone n'a que des angles de 120°, donc les côtés opposés sont parallèles.
La distance entre les côtés opposés a et a' peut se calculer en faisant b*rac(3)/2 + c'*rac(3)/2 ou en faisant b'*rac(3)/2 + c*rac(3)/2 (en raisonnant avec des triangles équilatéraux).
Donc b+c'=b'+c
De même, a+b'=a'+b et a+c'=a'+c

Cela revient donc à chercher les sous-ensembles {a,b,c,a',b',c'} de {1,...,9} tels que :
(1) b'-a'=b-a
(2) c'-a'=c-a

Je continue plus tard.

Franky1103 · #9

Voici la liste de mes 53 gâteaux hexagonaux, sans doublons par rotation ou symétrie (vérification faite):
145236 146237 147238 148239 145327 146328 147329
156247 157248 158249 153426 156429 167258 168259
165347 167349 165438 163527 164528 178269 176358
174538 173628 174629 187369 186459 184639 183729
256347 257348 258349 256438 257439 267358 268359
264537 278369 276458 276549 274638 275639 287469
285649 284739 367458 368459 367549 378469 375648
387569 385749 478569 486759
Mais si tu veux bien, Vasimolo, tu peux m'envoyer ta liste de 50 gâteaux par MP et je regarderai s'il manque des configurations sur ta liste ou, plus probablement, si des doublons m'ont échappé sur la mienne.
A+

Vasimolo · #10

OK , j'ai compris où est la différence dans nos décomptes

J'ai compté une seule fois les gâteaux 478569 et 486759 car ils utilisent les mêmes baguettes . Le plus simple est de noter les baguettes non utilisées , ces deux gâteaux seraient alors numérotés 123 .

Vasimolo

golgot59 · #11

Bah, j'ai déjà trouvé 2 erreurs !

Difficile de faire un exposé agréable à lire

Cas n°1 :

Il y a 22 combinaisons gagnantes si on prélève à tous les coups la barre 9 (voir la liste corrigée dans mon précédent post #3)

L'ensemble des combinaisons possibles est combin(8;6)=28.

Pour info, les 6 combinaisons que le pâtissier ne peut pas réaliser sont :
145678 (manque 239)
134678 (259)
124678 (359)
123578 (469)
123568 (479)
123458 (679)

Pour le cas général, je trouve 49 cas réalisables parmi combin(9;6)=84.
Liste des bâtons enlevés :123 124 125 126 127 128 129 135 137 138 139 145 147 148 149 156 159 167 168 169 179 189 237 245 249 257 258 269 279 289 345 347 349 358 367 369 378 379 389 456 459 489 567 568 569 579 589 689 789)

Si le client choisi de retirer le bâton 1, alors le pâtissier peut retirer le bâton 2 ou le 9 indifféremment, il pourra alors toujours créer un gâteau. Exemple si le client retire le 1 et le pâtissier le 2 : Si le client retire en dernier le :
3 : 98 76 54 (écart de 1)
4 : 97 86 53 (écart de 2)
5 : 98 76 43 (écart de 1)
6 : 95 84 73 (écart de 4)
7 : 98 65 43 (écart de 1)
8 : 97 64 53 (écart de 2)
9 : 87 65 43 (écart de 1)

Je ne vais pas faire tous les cas car c'est hyper long, mais je peux montrer le cas où le client commence par 3.
Si le pâtissier prend le 1 : 5 cas favorables
2 : 98 76 54 (écart de 1)
4 : impossible
5 : 97 86 42 (écart de 2)
6 : impossible
7 : 95 84 62 (écart de 4)
8 : 96 74 52 (écart de 3)
9 : 86 75 42 (écart de 2)

Si le pâtissier prend le 2 : 2 cas favorables
1 : 98 76 54 (écart de 1)
4 : impossible
5 : impossible
6 : impossible
7 : 96 85 41 (écart de 3)
8 : impossible
9 : impossible

Si le pâtissier prend le 4 : 3 cas favorables
1 : impossible
2 : impossible
5 : 98 76 21 (écart de 1)
6 : impossible
7 : 98 65 21 (écart de 1)
8 : impossible
9 : 87 65 21 (écart de 1)

Si le pâtissier prend le 5 : 3 cas favorables
1 : 97 86 42 (écart de 2)
2 : impossible
4 : 98 76 21 (écart de 1)
6 : impossible
7 : impossible
8 : 94 72 61 (écart de 5)
9 : impossible

Si le pâtissier prend le 6 : 2 cas favorables
1 : impossible
2 : impossible
4 : impossible
5 : impossible
7 : 98 54 21 (écart de 1)
8 : impossible
9 : 87 54 21 (écart de 1)

Si le pâtissier prend le 7 : 6 cas favorables
1 : 95 84 62 (écart de 4)
2 : 95 85 41 (écart de 3)
4 : 98 65 21 (écart de 1)
5 : impossible
6 : 98 54 21 (écart de 1)
8 : 95 62 51 (écart de 4)
9 : 84 62 51 (écart de 4)

Si le pâtissier prend le 8 : 4 cas favorables
1 : 96 74 52 (écart de 3)
2 : impossible
4 : impossible
5 : 94 72 61 (écart de 5)
6 : impossible
7 : 96 52 41 (écart de 3)
9 : 76 54 21 (écart de 1)

Si le pâtissier prend le 9 : 5 cas favorables
1 : 86 75 42 (écart de 2)
2 : impossible
4 : 87 65 21 (écart de 1)
5 : impossible
6 : 87 54 21 (écart de 1)
7 : 84 62 51 (écart de 4)
8 : 76 54 21 (écart de 1)

Conclusion, pour le cas où le client prend le bâton 3, le pâtissier a intérêt à choisir le bâton 7.

Les autres résultats (légèrement modifiés après édition) donne la même suite que dans mon post #6.

Au niveau proba, ça donne (7+7+6+5+5+5+6+7+7)/(7*9)=55/63 (environ 87.3%) contre 78,6% avec la stratégie première !

Vasimolo · #12

j'ai la même liste de gâteaux que toi

Pour la probabilité , c'est assez simple , il suffit de compter le nombre de troisièmes choix donnant une position gagnante pour chaque paire de bâton . Le choix du pâtissier se fixera alors sur l'un de ceux qui en donne le plus .

Je ne trouve pas la même probabilité que toi dans les deux cas .

Vasimolo

PS : j'ajoute un peu de temps car les calculs sont un peu longs .

Franky1103 · #13

Seules les baguettes non utilisées entrent effectivement en compte, peu importe
la géométrie des gâteaux. J'ai 49 configurations gagnantes (sur 84) qui sont:
123 124 125 126 127 128 129 135 137 138 139
145 147 148 149 156 159 167 168 169 179 189
237 245 249 257 258 269 279 289 345 347 349
358 367 369 378 379 389 456 459 489 567 568
569 579 589 689 789
Avec la stratégie proposée, la probabilité que le pâtissier gagne est de:
(1/3)x(7/7) + (2/3)x(5/7) = 17/21
Je reviendrai plus tard pour une éventuelle amélioration de cette stratégie.

golgot59 · #14

Ah ! Ça y est, je vois où je me suis trompé : Dans la méthode de calcul.

Cas 1 : Tous les tirages ne sont pas équiprobables puisque si le client choisi le 9, alors le pâtissier n'en prend pas 1 au hasard mais prend le 1 !

Du coup on a comme :
couples de départ ; fréquence d'apparition ; proba de gagner dans ce cas.
19 ; 1/9 ; 7/7 (100%)
29 ; 1/9 ; 5/7
39 ; 1/9 ; 5/7 (cas détaillé dans un de mes posts plus haut)
49 ; 1/9 ; 5/7
59 ; 1/9 ; 5/7
69 ; 1/9 ; 5/7
79 ; 1/9 ; 5/7
89 ; 1/9 ; 7/7
91 ; 1/9 ; 7/7

Finalement la proba de gagner dans le premier cas est : 6*1/9*5/7+3*1/9*7/7 = 51/63 = 17/21 = 80.95%

Cas 2 : Les couples donneraient :
1/9 : 7/7
2/1 : 7/7
3/7 : 6/7
4/9 : 5/7
5/9 : 5/7
6/9 : 5/7
7/3 : 6/7
8/9 : 7/7
9/1 : 7/7

Finalement la proba de gagner dans le deuxième cas est : 3*1/9*5/7+2*1/9*6/7 + 4*1/9*7/7 = 55/63 = 87.30%. Et là, je ne vos pas d'erreur... (D'autant que ma suite de probas est symétrique, ce qui semble assez logique)

Vasimolo · #15

C'est bon Franky et Golgot

Maintenant il existe une stratégie qui divise par 2 les chances de perdre .

Vasimolo

Franky1103 · #16

En restant sur les bâtons 1 et 9, si le client retire respectivement le bâton 2, 4 ou 6; 1 ou 8 et 3, 5, 7 ou 9, alors le pâtissier retire respectivement le bâton 1; 9 et indifféremment 1 ou 9, alors la probabilité de gagner pour ce dernier est de:
(4/9)x(7/7) + (2/9)x(6/7) + (3/9)x(5/7) = 55/63
Je trouve une probabilité de perdre de 8/63, soit les 2/3 de la précédente (4/21), mais pas la moitié attendue.

Edit: A la suite d'une erreur, ma stratégie est fausse (je n'ai pas écrit la nouvelle ici), mais ma probabilité reste inchangée à 55/63.

golgot59 · #17

A partir des mêmes règles du jeu : Client/chef/client et des mêmes longueurs de bâton, je ne vois pas comment faire mieux que dans le cas 2 à 87.30%...

Ta stratégie dépasse les 90% ?

Vasimolo · #18

J'avais un peu mieux sans astuce particulière, il s'agit donc certainement d'une erreur de calcul , je vérifierai

Vasimolo

Vasimolo · #19

Il me manquait un cas , nous sommes donc d'accord Golgot

Vasimolo

golgot59 · #20

Ouf !

Je me voyais mal re-re-re-re-vérifier !

Merci pour ce gâteau que j'ai pris plaisir à analyser !

titoufred · #21

Je ne trouve que 49 "écartages" de tiges possibles permettant de construire un gâteau :

Code:

123,124,125,126,127,128,129,135,137,138,139,145,147,148,149,156,159,167,168,169,179,189,237,245,249,257,258,269,279,289,345,347,349,358,367,369,378,379,389,456,459,489,567,568,569,579,589,689,789

Je ne vois pas de 50ème !

titoufred · #22

Dans cette liste des écartages gagnants, on compte combien de fois apparait chaque couple de baguettes :

Code:

12 : 7 // 13 : 5 // 14 : 5 // 15 : 5 // 16 : 5 // 17 : 5 // 18 : 5 // 19 : 7 
21 : 7 // 23 : 2 // 24 : 3 // 25 : 4 // 26 : 2 // 27 : 4 // 28 : 3 // 29 : 5 
31 : 5 // 32 : 2 // 34 : 3 // 35 : 3 // 36 : 2 // 37 : 6 // 38 : 4 // 39 : 5
41 : 5 // 42 : 3 // 43 : 3 // 45 : 5 // 46 : 1 // 47 : 2 // 48 : 2 // 49 : 5 
51 : 5 // 52 : 4 // 53 : 3 // 54 : 5 // 56 : 5 // 57 : 3 // 58 : 4 // 59 : 5
61 : 5 // 62 : 2 // 63 : 2 // 64 : 1 // 65 : 5 // 67 : 3 // 68 : 3 // 69 : 5
71 : 5 // 72 : 4 // 73 : 6 // 74 : 2 // 75 : 3 // 76 : 3 // 78 : 2 // 79 : 5 
81 : 5 // 82 : 3 // 83 : 4 // 84 : 2 // 85 : 4 // 86 : 3 // 87 : 2 // 89 : 7
91 : 7 // 92 : 5 // 93 : 5 // 94 : 5 // 95 : 5 // 96 : 5 // 97 : 5 // 98 : 7

Ce qui nous donne donc la tactique optimale de réponse pour le boulanger :

à 1 répondre 9 (proba de gagner : 7/7)
à 2 répondre 1 (proba de gagner : 7/7)
à 3 répondre 7 (proba de gagner : 6/7)
à 4 répondre 1 (proba de gagner : 5/7)
à 5 répondre 1 (proba de gagner : 5/7)
à 6 répondre 1 (proba de gagner : 5/7)
à 7 répondre 3 (proba de gagner : 6/7)
à 8 répondre 9 (proba de gagner : 7/7)
à 9 répondre 1 (proba de gagner : 7/7)

Ce qui fait donc une probabilité totale de gagner de 55/63.

C'est mieux que la tactique initiale du boulanger qui ne le faisait gagner qu'avec une probabilité de 51/63.

Vasimolo · #23

Un petit schéma de la méthode de résolution de Golgot qui est aussi la mienne .

En prolongeant les côtés d'un gâteau on obtient un triangle équilatéral donc la différence entre deux côtés opposés est constante . Réciproquement , on vérifie facilement que si cette condition est réalisée alors le gâteau existe . Il n'y a plus qu'à compter les gâteaux en faisant varier cette différence de 1 à 6 , on trouve alors 49 gâteaux à condition de ne compter qu'une seule fois les gâteaux utilisant les mêmes baguettes . On désigne les gâteaux par les baguettes non utilisées par exemple le gâteau 123 est fabriqué avec les baguettes 456789 . Il y a en tout 84-49=35 gâteaux irréalisables . On cherche ensuite pour chaque paire de baguettes retirées quel est le nombre de gâteaux irréalisables :

19 : aucun
29 : 2
39 : 2
49 : 2
59 : 2
69 : 2
79 : 2
89 : 0
91 : 0

La stratégie du pâtissier donne donc une probabilité de perte de 12/63 .

Si on choisit maintenant pour chaque baguette , une baguette donnant un minimum de gâteaux irréalisables :

1 : 2 ou 9 pour 0 gâteau .
2 : 1 pour 0 gâteau .
3 : 7 pour 1 gâteau .
4 : 1 ou 5 ou 9 pour 2 gâteaux .
5 : 1 ou4 ou 6 ou 9 pour 2 gâteaux .
6 : 1 ou 5 ou 9 pour 2 gâteaux .
7 : 3 pour 1 gâteau .
8 : 9 pour 0 gâteau .
9 : 1 ou 8 pour 0 gâteau .

La stratégie donne une probabilité de perte de 8/63 .

Le pâtissier peut choisir , par exemple , d'associer les baguettes {1;2},{3;7} et {8;9} par paires ( c'est à dire que le choix d'une baguette de la paire entraine le choix de la deuxième ) et d'associer les 3 dernières à 1 ou 9 .

Il y a peut-être une façon plus synthétique d'aborder le problème ???

Merci pour la participation

Vasimolo

PS : je n'avais pas vu le message de Titoufred quand j'ai posté ma réponse : sa méthode est grosso-modo la même

Forum dédié aux énigmes et à toutes formes de jeux de logique.	Déconnexion
Tu n'es pas identifié sur Prise2tete : s'identifier. Accueil Forum	[+]

#1 - 12-10-2014 18:48:23

Gâtau 81

#0 Pub

#2 - 13-10-2014 22:48:57

gâtzau 81

#3 - 13-10-2014 23:19:21

GGâteau 81

#4 - 14-10-2014 00:08:17

gâtzau 81

#5 - 14-10-2014 00:52:51

Gtâeau 81

#6 - 14-10-2014 01:06:40

âGteau 81

#7 - 14-10-2014 10:03:28

Gteau 81

#8 - 14-10-2014 11:12:04

Gâtteau 81

#9 - 14-10-2014 14:53:21

Gâteua 81

#10 - 14-10-2014 15:35:48

Gâetau 81

#11 - 14-10-2014 22:36:39

âteau 81

#12 - 15-10-2014 10:14:50

gâteai 81

#13 - 15-10-2014 10:51:51

Gâtea 81

#14 - 15-10-2014 16:00:34

âGteau 81

#15 - 15-10-2014 17:03:08

gâyeau 81

#16 - 15-10-2014 19:26:09

Gâteu 81

#17 - 15-10-2014 20:56:34

Gâetau 81

#18 - 15-10-2014 21:27:25

gâtrau 81

#19 - 16-10-2014 18:37:36

hâteau 81

#20 - 16-10-2014 18:56:07

Gâteau 8

#21 - 16-10-2014 22:05:11

fâteau 81

Code:

#22 - 16-10-2014 22:37:30

âteau 81

Code:

#23 - 16-10-2014 22:44:36

gâtrau 81

Réponse rapide

Sujets similaires

Mots clés des moteurs de recherche

Pied de page des forums