|
#1 - 29-12-2011 11:14:10
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3839
dénouzr l'écheveau
Bonjour à tous.
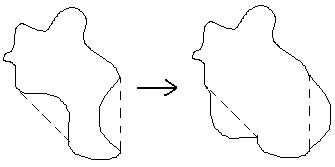
Si vous tracez une boucle sans croisement ni levée de crayon, avec autant de courbes et d'arabesques que votre talent artistique vous permet, et qu'on vous demande ensuite d'en tirer une courbe convexe de même longueur (on vous pardonnera vos petites imperfections éventuelles) comment vous y prendriez vous ?
Bon amusement
#2 - 29-12-2011 11:26:47
- Jackv
- Elite de Prise2Tete
- Enigmes résolues : 34
- Messages : 3609
- Lieu: 94110
dénouer k'écheveau
Les croisements sont-ils admis sur la courbe résultante ?
Si oui, je commence par repérer les n points d'inflexion sur ma courbe, déterminant ainsi n+1 tronçons.
A l'aide d'un papier calque, je recopie le premier tronçon, je retourne la feuille pour calquer le 2ème en respectant autant que possible la tangence et ainsi de suite jusqu'au dernier.
EDIT : Si non, mais c'est un peu plus long, je découpe en morceaux plus petits, et je commence par ceux dont la courbure est la plus grande, en retournant la feuille de calque quand la courbure s'inverse, et j'obtiens une courbe qui va ressembler à une spirale, mais ce n'est pas une boucle fermée ... 
#3 - 29-12-2011 11:57:09
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3839
Dénouer l'écheveeau
L'idée est bien là, mais je le fais sans croisement.
#4 - 29-12-2011 12:21:02
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
dénouer l'écheveay
En considérant l'enveloppe convexe de l'ensemble puis en prenant le symétrique de chaque partie à l'intérieur par rapport au côté sur lequel elle s'appuie et en renouvelant l’opération autant de fois qu'il le faut on doit pouvoir y arriver .
Mais bon , ce n'est pas une preuve 
Vasimolo
#5 - 29-12-2011 12:32:47
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3839
Dénouer l'éheveau
La courbe a tout de même un périmètre donné.....
On dira que cette fonction a une limite.
#6 - 29-12-2011 15:52:08
- halloduda
- Professionnel de Prise2Tete
- Enigmes résolues : 24
- Messages : 495
- Lieu: Ardèche
Dénoure l'écheveau
Partant d'une courbe concave, je prendrais une "tangente" "externe" à la courbe.
Cette "tangente" ne recoupe pas la courbe, elle a deux points de contact (au moins).
Prenons deux de ces points : cela définit deux parties de la courbe.
Je remplacerais la partie de la courbe la plus "proche" de la tangente
par sa symétrique par rapport à la tangente, la mettant ainsi "à l'extérieur".
J'obtiens ainsi une autre courbe :
- qui a la même longueur que l'originale
- qui est également réalisable sans lever de crayon et
- dont la surface interne a strictement augmenté.
- qui est également convave, sauf éventuellement si les points de contact
sont de sommets.
Et ainsi de suite...
La suite des surfaces obtenues est strictement croissante et majorée par [latex]\frac{l^2}{4\pi}[/latex].
(au mieux, c'est un cercle)
Il y a donc convergence.
Mais le nombre d'opérations est, semble-t-il, infini, sauf si la courbe a des sommets.
#7 - 29-12-2011 18:39:13
- shadock
- Elite de Prise2Tete
- Enigmes résolues : 39
- Messages : 3334
dénouet l'écheveau
Serait-il possible d'avoir un exemple de avant et après en image parce que je ne comprends pas l'énoncé? 
"L'expérience est une lanterne qui n'éclaire que celui qui la porte." L-F. Céline
#8 - 29-12-2011 18:53:14
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3839
dénouzr l'écheveau
@shadock: une boucle sans croisement ni levée de crayon, c'est pas bien compliqué: une ligne quelconque qui part d'un point et y revient sans avoir jamais recouper ni même toucher sa propre trace. ça laisse beaucoup de place à la fantaisie. Quant à l'après.....à toi de voir.
#9 - 29-12-2011 22:04:44
- shadock
- Elite de Prise2Tete
- Enigmes résolues : 39
- Messages : 3334
Dénouer l'cheveau
Si ça j'avais compris c'est la suite et je pense ne pas avoir le niveau.
"L'expérience est une lanterne qui n'éclaire que celui qui la porte." L-F. Céline
#10 - 30-12-2011 02:13:36
- Grizix
- Habitué de Prise2Tete
- Enigmes résolues : 30
- Messages : 31
Dénoer l'écheveau
Je déroule une ficelle sur ma courbe non convexe. Il ne me reste plus qu'à convexifier (si je puis me permettre) ma ficelle , puis à la tendre à l'aide de punaises pour tracer la courbe convexe. Pas très mathématique, mais efficace non ?
#11 - 30-12-2011 23:12:03
- irmo322
- Professionnel de Prise2Tete
- Enigmes résolues : 36
- Messages : 203
dénouer l'écheveay
Salut,
ton énigme n'est pas claire pour moi, tu veux dire quoi par "tirer" une courbe convexe de même longueur?
#12 - 31-12-2011 14:26:54
- w9Lyl6n
- Professionnel de Prise2Tete
- Enigmes résolues : 26
- Messages : 239
#13 - 31-12-2011 18:10:37
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3839
Dénouer 'écheveau
Bonne réflexion Mathieu.
Si la courbe est une ligne brisée avec un nombre fini de segments, pour moi, ça se "convexifie" à 100%. Avec un nombre fini de segments je dis bien.
#14 - 01-01-2012 11:06:43
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3839
fénouer l'écheveau
Merci aux participants.
A peu près tout le monde a vu qu'il fallait redessiner les symétriques des parties intérieures à partir des tangentes extérieures. Tous avez fait aussi la remarque de l'imperfection de la convexité finale.
En fait, s'il s'agissait d'une ligne brisée, on obtiendrait obligatoirement la convexité parfaite, car dans les opérations successives, on n'augmente pas le nombre de segments.
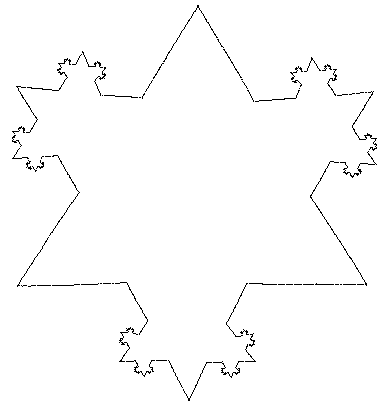
Pour les courbes, c'est différent, car dans une opération on crée 2 changements de courbe. Donc plus on fait d'opérations, plus on crée des parties concaves, celles ci étant de plus en plus courtes et de plus en plus fines, jusqu'à devenir imperceptibles.
Mots clés des moteurs de recherche
|
 |

 Accueil
Accueil
 Forum
Forum