 |
#1 - 07-01-2012 16:16:19
- titoufred
- Elite de Prise2Tete
- Enigmes résolues : 20
- Messages : 1749
Le nommbre mystère
J'ai choisi secrètement un nombre entre 1 et 99.
Vous devez essayer de le deviner en faisant des propositions.
Attention, si une proposition dépasse le nombre mystère, cela compte comme une erreur nommée "dépassement", et vous n'avez le droit qu'à 3 erreurs de dépassement !
Quelle stratégie adopter pour être sûr de trouver le nombre mystère en un minimum de propositions ?
#2 - 08-01-2012 02:08:23
- Grizix
- Habitué de Prise2Tete
- Enigmes résolues : 30
- Messages : 31
Le nombre mysère
Dichotomie jusqu'à trouver ou atteindre 3 dépassements, puis incrémentation. Lors de la phase de dichotomie, on arrondi à l'inférieur. Pire cas, 11, 14 propositions :
50-25-12-1-2-3-4-5-6-7-8-9-10-11
#3 - 08-01-2012 02:19:43
- titoufred
- Elite de Prise2Tete
- Enigmes résolues : 20
- Messages : 1749
L nombre mystère
Bravo à Grizix, qui est le premier à proposer une stratégie qui assure de trouver le nombre mystère en Spoiler : [Afficher le message] 14 coups maximum.
Il est possible de faire mieux.
#4 - 08-01-2012 07:59:54
- TiLapiot
- Expert de Prise2Tete
- Enigmes résolues : 16
- Messages : 852
- Lieu: au terrier ;^)
le nombrz mystère
Bjr titoufred,
Je procéderai par dichotomies successives. Soit X ton nombre secret.
Je te demande 1/ X est-il >= à 50 ?
Si ta réponse 1/ est OUI, je te demande 2/ X est-il >= à 75 ?
Si ta réponse 2/ est OUI, je te demande 3/ X est-il >= à 88 ?
Si ta réponse 3/ est OUI, je te demande 4/ X est-il = à 88 ?
Si ta réponse 4/ est NON, je te demande 5/ X est-il = à 89 ?
Si ta réponse 5/ est NON, je te demande 6/ X est-il = à 90 ?
etc jusqu'à 99, jusqu'à avoir trouvé.
Par contre, ...
Si ta réponse 1/ est NON, c'est mon 1er dépassement,
je te demande 2/ X est-il >= à 25 ?
Si ta réponse 2/ est OUI, je te demande 3/ X est-il >= à 38 ?
Si ta réponse 2/ est NON, 2nd dépassement,
je te demande 3/ X est-il >= à 12 ?
Avec cette méthode, on doit y arriver en une quinzaine d'essais, mais même si c'est sûrement pas le record minimal, il n'y a pas le feu au lac 
#5 - 08-01-2012 10:20:11
- titoufred
- Elite de Prise2Tete
- Enigmes résolues : 20
- Messages : 1749
Le nombre mytsère
Tilapiot, tu as trouvé la même solution que Grizix.
On peut faire bien mieux.
#6 - 08-01-2012 10:39:39
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3834
lz nombre mystère
Si l'on propose une dichotomie classique, c'est assez rapide, en 7 ou 8 coups. On n'a pas le droit de s'en servir ?
#8 - 08-01-2012 13:08:19
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 6,177E+3
Le nombre mystèr
En 7 il je ne vais que jusqu'à 98 , il me faut donc un 8 ème coup...
#9 - 08-01-2012 15:16:17
- titoufred
- Elite de Prise2Tete
- Enigmes résolues : 20
- Messages : 1749
Le nombre mystèr
Tout à fait Clydevil !
Mais connaître la réponse à l'énigme que tu mentionnes ne suffit pas...
#10 - 08-01-2012 17:18:12
- Clydevil
- Expert de Prise2Tete
- Enigmes résolues : 29
- Messages : 914
- Lieu: Seahaven island
Le nombre myystère
Mais connaître la réponse à l'énigme que tu mentionnes ne suffit pas...
Mouarf ça dépend ce que veut dire connaître ;p il y a "mal connaître" et il y a avoir résolu pour n sphères de cristal (ce qui n'est pas nécessairement plus dur comme récurrence), quand n tend vers l'infini le protocole tendra vers une simple dichotomie, pour un n quelconque c'est une structure fractale non symétrique.
Je l'avais résolu pour n quelconque, ici n=3, malheureusement j'ai perdu mes notes et suis du genre extrêmement flemmard :p.
Cela dit, énigme très intéressante! c'est beau de voir qu'avec des énoncés simples on peut avoir des structures déjà complexes.
#11 - 08-01-2012 20:10:26
- titoufred
- Elite de Prise2Tete
- Enigmes résolues : 20
- Messages : 1749
le nombre mystèrz
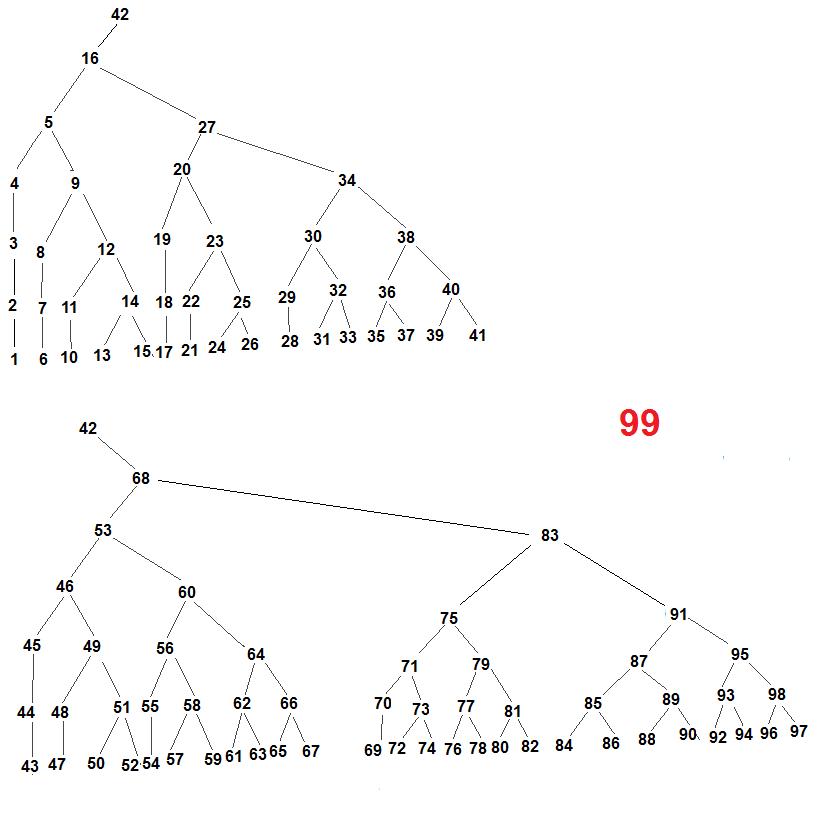
Bravo à gwen27, qui a donné une stratégie permettant de trouver le nombre mystère en Spoiler : [Afficher le message] 8 coups au maximum.
#12 - 08-01-2012 20:12:06
- titoufred
- Elite de Prise2Tete
- Enigmes résolues : 20
- Messages : 1749
le nombre myqtère
@nodgim : on ne peut pas faire une dichotomie classique car on n'a le droit qu'à 3 erreurs de dépassement.
#13 - 09-01-2012 11:22:03
- Clydevil
- Expert de Prise2Tete
- Enigmes résolues : 29
- Messages : 914
- Lieu: Seahaven island
le nolbre mystère
Du coup j'ai ressorti mon petit prog de derrière les fagots pour être sur, et avec 8 coup et 3 dépassements il me semble qu'on ne peut trouver le nombre mystère que si celui ci est entre 0 et 92 compris.
(Et ca commence par tenter 29 et en cas d'échec tenter 7.)
Ça fait très peu de lignes:
Renvoie le nombre max d'entiers parmi lesquels on peut trouver le nombre mystère en nCoups coups et avec nTry dépassements:
int etages(int nCoups, int nTry)
{
if (nCoups==1) return 1;
if (nTry==1) return nCoups;
return etages(nCoups-1,nTry)+1+etages(nCoups-1,nTry-1);
}
Par contre en 9 coups et 3 dépassements on le trouve s'il se trouve entre 0 et 129.
Donc j'aurais dit 9 et non 8.
Je me suis planté quelque part?
#14 - 09-01-2012 12:03:42
- TiLapiot
- Expert de Prise2Tete
- Enigmes résolues : 16
- Messages : 852
- Lieu: au terrier ;^)
lr nombre mystère
"Attention, si une proposition dépasse le nombre mystère, cela compte comme une erreur nommée dépassement"
Peut-on poser des questions du genre "1°) TON NOMBRE EST-IL PAIR ?" ?
ou "2°) TON NOMBRE EST-IL MULTIPLE DE TROIS ?"
ou "3°) LE LOGARITHME DE TON NOMBRE EST-IL SUPÉRIEUR À 2 ?"
Si oui, ça pourrait (?) permettre d'élaguer les possibilités...
#15 - 09-01-2012 12:38:36
- titoufred
- Elite de Prise2Tete
- Enigmes résolues : 20
- Messages : 1749
Le nombre mstère
@Clydevil : Oui, c'est ça mais avec nTry==0 pour le deuxième test. On pourrait deviner un nombre mystère compris entre 1 et 162 avec 8 propositions.
@TiLapiot : Non, on ne peut pas poser des questions de ce genre, on peut juste proposer un nombre. Et les réponses seront "plus grand", "plus petit" ou "trouvé".
#16 - 09-01-2012 14:14:48
- Clydevil
- Expert de Prise2Tete
- Enigmes résolues : 29
- Messages : 914
- Lieu: Seahaven island
le nombre mustère
@Clydevil : Oui, c'est ça mais avec nTry==0 pour le deuxième test.
C'est ca la différence en fait avec le truc des sphère de cristal, c'est que dans le cas des sphères on doit aller jusqu'au dépassement pour déterminer que c'est l'étage fatidique, alors que la ca dit "trouvé" avant 
En effet, petite nuance, au temps pour moi.
On pourrait deviner un nombre mystère compris entre 1 et 162 avec 8 propositions.
Je confirme et on commence en 93.
Merci pour cette variante.
#17 - 09-01-2012 16:48:24
- rivas
- Elite de Prise2Tete
- Enigmes résolues : 48
- Messages : 1106
- Lieu: Jacou
ke nombre mystère
La stratégie comme par 3 trichotomies en annonçant à chaque fois le premier tiers.
On commence donc par 33.
Si 33 est trop grand cela fait un dépassement, on va trissecter [1,32] et on annonce 11 sinon on trissecte [34-99] et on annonce 56.
Après les trichotomies, soit on a déjà 3 dépassements ce qui veut dire qu'on est tombé 3 fois trop grand et l'intervalle qui reste est très petit (33, 11, 4), reste à essayer 1,2,3.
Soit on n'a pas 3 dépassements et on peut effectuer au moins (3-le nombre de dépassement déja atteints) dichotomies ce qui donne aussi un intervalle assez petit pour être testé un par un.
En cas de longueur impaire, on coupe l'intervalle [N/N+1] (et non pas [N+1/N]).
Le maximum de coup est de 8.
Exemple: Le nombre à trouver est 60.
1-Je demande 33: trop petit. Reste l'intervalle [34-99], L=66.
2- Je demande 55: trop petit. Reste l'intervalle [56-99], L=44.
3- Je demande 70: trop grand. Reste l'intervalle [56-69], L=14
Je peux faire au plus 2 dichotomies:
4-Je demande 63: trop grand. Reste l'intervalle [56-62], L=7
5-Je demande 59: trop petit. Reste l'intervalle [60-62].
Je peux les demander 1 par 1 en partant du plus petit donc sans dépassement en 3 coups donc 8 max au total.
Je peux aussi faire encore 1 dichotomie puisqu'il me reste un dépassement: 61 trop grand et donc 60.
Exemple: Le nombre à trouver est 97
1-33: trop petit. Reste [34-99], L=66.
2- 55: trop petit. Reste [56-99], L=44.
3- 70: trop petit. Reste [71-99], L=29
Les dichotomies:
4- 85: trop petit: Reste [86-99], L=14
5- 92: trop petit: Reste [93-99], L=7
6- 96: trop petit: Reste [97-99], L=3
7- 98: trop petit
8- 99
En fait la longueur de l'intervalle maximum est le suivant (toujours arrondi à l'entier supérieur):
Après la première trichotomie: 2/3*99-1=65
Après la seconde trichotomie: 2/3*65-1=43
Après la troisième trichotomie: 2/3*99-1=28
Puis 3 dichotomies qui donnent:
28/2-1=13
13/2-1=6
6/2-1=2
Il reste donc 2 nombres à tester au pire. On commence par le plus petit.
Il y a donc au maximum 8 coups à jouer.
#18 - 09-01-2012 17:26:30
- titoufred
- Elite de Prise2Tete
- Enigmes résolues : 20
- Messages : 1749
Le onmbre mystère
@Rivas :
voici ton exemple donné pour 97 :
Spoiler : [Afficher le message] 33, 55, 70, 85, 92, 96, 98(*), 97
si je suis la stratégie que tu as énoncée, il me semble que 73 nécessite 9 propositions non ?
Spoiler : [Afficher le message] 33, 55, 70, 85(*), 78(**), 74(***), 71, 72, 73.
#19 - 09-01-2012 18:03:46
- rivas
- Elite de Prise2Tete
- Enigmes résolues : 48
- Messages : 1106
- Lieu: Jacou
le nomvre mystère
Après le coup 4/85: trop grand, il reste [71-84], L=14. On partage L en 6,1,7 et on prend donc 77.
5/77: trop grand: il reste [71-76], L=6. On partage en 2,1,3.
6/73: fini.
Ceci étant dit, je pense que ma suite des 3 premiers devrait être 34, 57, 72 pour respecter la règle ci-dessous.
En effet, il est important de partager en un intervalle de longueur N en 2 en N-1/2,1,N-1/2 ou N/2-1,1,N/2.
Et en 3 en N,1,N,N-1 ou N,1,N-1, N-1.
Mais dans tous les cas, le premier intervalle le plus long.
Dans ce cas, l'exemple 73 devient:
34, 57, 72.
Il reste [73-99], L=27 (cas le plus défavorable).
86(*), il reste [73-85], L=13
79(*), il reste [73-78], L=6
75(*), il reste [73-74], à tester en 2 coups (donc 8 max) du plus petit au plus grand.
L'exemple 97 devient:
34,57,72,86,93,96,98(*),97
L'exemple 60 devient:
34,57,72(*),64(*),60
Par ailleurs, quand il n'en reste que 3 et qu'on a encore un dépassement possible, on optimise bien sûr en choisissant celui du milieu.
Attention, tout le monde voyant tes commentaires, cela peut donner des indices 
#20 - 09-01-2012 18:15:42
- Zindy
- Professionnel de Prise2Tete
- Enigmes résolues : 48
- Messages : 107
Le nombre mysètre
Première constatation, arrivé à 3 erreurs de dépassements, il faut commencer en bas de la plage des possibilités restantes et remonter de 1 en 1, on est ainsi sûr de trouver la réponse sans un quatrième dépassement. Du coup, si jamais il reste N nombres dans la plage des possibilités restantes, il faut donc au pire-cas N tentatives pour tomber dessus. Il faut donc minimiser le nombre de possibilités restantes à l'issue des 3 erreurs.
Autrement dit, une fois qu'on a eu nos 3 dépassements, il faut bourrinement balayer tous les cas restant, alors que tant qu'il nous reste des possibilités d'erreur, on peut taper par pallier.
La dichotomie n'est pas la meilleure solution, car si on propose 50 en premier choix, selon qu'on est en dépassement ou non, il nous reste en gros 50 cas possibles à étudier, sauf que dans un des cas, on n'a plus que deux "cartouches dépassement" à user pour resserrer les choix parmi 50, alors que dans l'autre cas, il nous reste 3 "cartouches dépassement" possibles toujours pour resserrer les choix parmi 50.
Il aurait donc mieux valu que dans le cas où on dépasse, il nous reste moins de cas que dans l'autre. Il faut donc que toute proposition laisse moins de cas possibles si on dépasse que si on ne dépasse pas.
D'où l'idée suivante : dans la plage des nombres possibles, proposer toujours le nombre qui marque le seuil du premier tiers de cette plage. Exemple, au départ, la plage couvre entre 1 et 99, on proposera donc 33 (le tiers de 99).
Là, si on dépasse, on sait que la solution est entre 1 et 32, on refait une proposition au tiers donc on propose 11 (le tiers de 32 arrondi sup).
Et si on ne dépasse pas, on sait que la solution est entre 34 et 99 (donc il reste 66 possibilités, mais on n'a toujours pas "grillé" de cartouche "erreur"), et on proposera 55 (seuil du premier tiers de la plage 34-99).
Le pire-cas correspond alors au nombre 99, qui nécessite 10 essais. C'est le pire-cas puisque ne tombant jamais sur une erreur, on ne réduit jamais le nombre de possibilités au tiers des possibilités restantes.
Les propositions sont alors : 33 OK, 55 OK, 70 OK, 80 OK, 87 OK, 92 OK, 95 OK, 97 OK, 98 OK, 99 FIN
Si on prend par exemple 69 (exemple complètement au hasard), voici le cheminement en 8 coups avec cette stratégie : 33 OK, 55 OK, 70 ERR, 60 OK, 64 OK, 66 OK, 68 OK, 69 FIN
#21 - 09-01-2012 18:21:19
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3834
eL nombre mystère
Je ne comprends pas très bien cette erreur de dépassement:
Je propose: le nombre mystère est inférieur à 50.
#22 - 09-01-2012 18:40:20
- titoufred
- Elite de Prise2Tete
- Enigmes résolues : 20
- Messages : 1749
Le nombre mysètre
@nodgim :
C'est comme le nombre mystère habituel, on te répond "plus grand", "trouvé" ou "plus petit". Sauf que tu n'as le droit d'entendre que 3 "plus petit". A la 4ème proposition dépassant le nombre mystère, tu as perdu.
@rivas : je suppose que ta solution marche comme ça oui. bravo. Elle permet de trouver le nombre mystère en Spoiler : [Afficher le message] 8 coups maximum.
Cependant, il y a une stratégie qui permet de trouver le nombre mystère en moins de coups que la tienne en moyenne.
#23 - 09-01-2012 19:04:58
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3834
le nombre mystèee
Est ce tjs vrai si la proposition ne porte pas directement sur un rang ?
Par exemple: le chiffre des dizaines est plus grand que le chiffre des unités ?
Ou encore: le nombre de diviseurs est supérieur à 6 ?
#24 - 09-01-2012 20:11:27
- titoufred
- Elite de Prise2Tete
- Enigmes résolues : 20
- Messages : 1749
Le nombre ystère
Faire une proposition, c'est proposer un nombre.
#25 - 10-01-2012 17:33:20
- rivas
- Elite de Prise2Tete
- Enigmes résolues : 48
- Messages : 1106
- Lieu: Jacou
le npmbre mystère
J'ai été intéressé par ce problème et donc je le suis par ses solutions.
J'ai la même stratégie que Zindy.
Je ne comprends pas très bien celle de Gwen. Si je regarde le graphe et que je choisis comme nombre 1, quelles sont les propositions? 42, 16, 5, 4, 3, 2, 1? Ou bien est-ce que je ne comprends pas comment utiliser le graphe?
Je ne comprends pas trop non plus la réponse de Clydevil. Peut-être que quelques exemples de suites pour quelques nombres donnés m'aideraient à mieux comprendre?
Merci d'avance.
Mots clés des moteurs de recherche
|
 |

 Accueil
Accueil
 Forum
Forum







