J'ai tapé le programme et pour chaque nombre N, le produit de a+c+1 par a-c vaut 2N. Par contre, je n'ai pas compris pourquoi ces deux nombres et non les autres.

Exemple : N=23, a+c+1 = 23 et a-c = 2 → c'est le seul cas (sans compter 1*46)
Mais N=24, a+c+1 = 16 et a-c = 3 → Mais il y a aussi 2*24, 4*12 ou 6*8

Mon programme me permet de montrer que (a+b+1)*(a-c)=2*N

Pour N=49999, mon programme met 1 milliseconde

Démonstration de la solution:
La solution est affichée si x=N or x=b-d donc N=b-d.
b est la somme des a premiers entiers à partir de 1 donc b=a*(a+1)/2
d aussi est la somme des c premiers entiers à partir de 1 donc d=c*(c+1)/2
[TeX]N=b-d=\frac{a*(a+1)}{2}-\frac{c*(c+1)}{2}\Rightarrow 2*N=a^2+a-c^2-c[/TeX][TeX]\Rightarrow 2*N=(a^2-c^2)+(a-c)[/TeX][TeX]\Rightarrow 2*N=(a+c)*(a-c)+(a-c)[/TeX]
[latex]\Rightarrow 2*N=(a-c)*(a+c+1)[/latex]  CQFD

Bonjour,

Après quelques essais, on remarque que le produit des nombres affichés est 2N.

Remarquons que avec les valeurs de départ nous avons :

a(a+1)/2 = b et c(c+1)/2 = d et x = b - d.
Il est facile de vérifier que ces égalités sont des invariants de boucles,
donc si le programme termine nous avons à la fin du programme :

N = x = b - d = a(a+1)/2 - c(c+1)/2, autrement écrit :
2N = a(a+1) - c(c+1) = a² - c² + a - c = (a+c)(a-c)+(a-c) = (a+c+1) (a-c).
Donc le produit des deux nombres affichés est bien égal à 2N.

Terminaison du programme :
Le programme termine pour N = 0.
Par définition des nombres triangulaires, nous avons pour tout N > 0, N(N-1)/2 + N = N(N+1)/2.

Autrement écrit, N = N(N+1)/2 - N(N-1)/2, après un peu de réflexion, on peut facilement se convaincre que si a atteint la valeur N, alors on passera dans l'étape 3) jusqu'à ce que c atteigne la valeur (N-1) et le programme terminera.
(c <= a est aussi un invariant de boucle). 

Maintenant, il est curieux de constaté que :
  i)le programme retourne (2N,1) lorsque N est une puissance de 2.
  ii)le programme retourne (N,2) lorsque N est premier.

En fait le ii) peut s'expliquer par le fait que si N est premier alors 2*N est la seul décomposition de 2N en facteur premier.

Sinon, à quoi correspondent plus précisément les deux nombres retournés, je ne sais pas

P.S.: pour N = 49999, j'ai un dixième de seconde. (et 49999 est premier )

Les temps de calcul:
2^31-1 (3115 ms),
2^31 (6370 ms),
3^31 (117 ms) et autres.

Il parait évident que le temps de calcul ne dépend pas ou pas seulement de la grandeur de N mais d'autres propriétés (par exemple sa décomposition en facteur de nombres premiers).

Il faut noter par ailleurs que ce temps dépend énormément des performances du pc, cela peut aller du simple au centuple voire plus d'un pc à un autre suivant leur performance

Bonjour,


Voici ce que je trouve pour les première valeurs de N avec un code tout nase en VBA excel ....



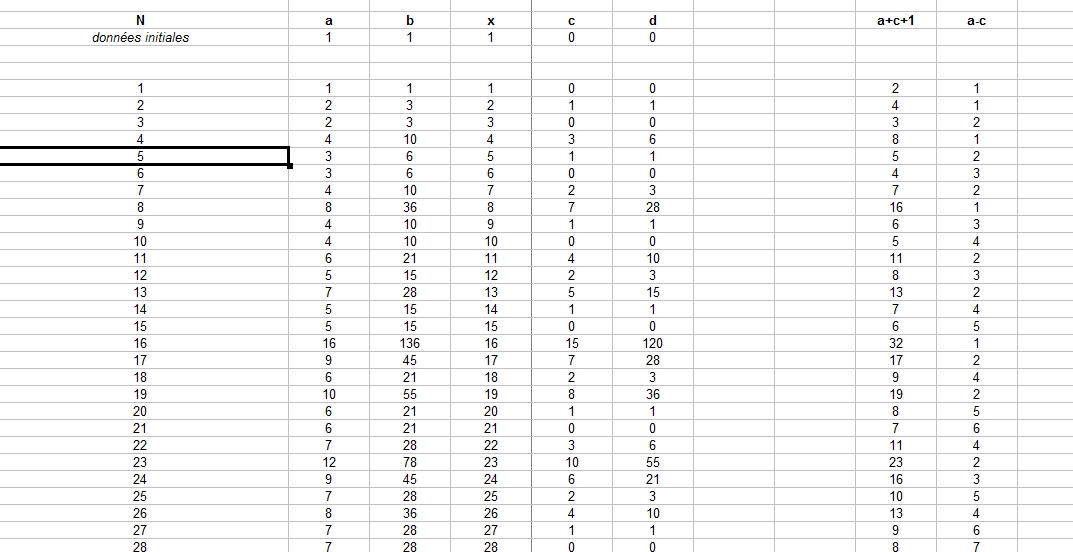
(copie d'écran zoomable)

Pourrais-tu confirmer que ce sont les valeurs attendues pour que je continue à me creuser la tête sur leur signification ?

Merci, bonne soirée !

Sub MACROTOTOP2T

dim a,b,x,c,d,N as double
dim ligne as double

FOR ligne= 21 TO 50000

cells(ligne,1).value=ligne-20
N=ligne-20
a=1
b=1
x=1
c=0
d=0



label1:

if x<N then 
a=a+1
b=b+a
x=b-d
goto label1
end if

if x>N then
c=c+1
d=d+c
x=b-d
goto label1
end if

if x=N then
cells(ligne,2).value=a
cells(ligne,3).value = b
cells(ligne,4).value=x
cells(ligne,5).value=c
cells(ligne,6).value=d

cells(ligne,9).value=a+c+1
cells(ligne,10).value=a-c
goto finmacro
end if


finmacro: 
next ligne
End sub

Les réponses de chacun étant affichées, je laisse à ceux qui n'ont pas encore trouvé la formule générale le soin de la lire dans les bons commentaires qui ont été faits et auxquels il n'y pas grand chose à ajouter.

Merci à tous les participants pour les efforts déployés, notamment pour l'écriture en réel du programme, et les résultats affichés des performances.

Les variables b et d renvoient aux nombre triangulaires, c'est à dire les nombres de la forme n(n+1)/2.
Tout le monde a vu que les 2 valeurs affichées donnent comme résultat 2 fois le nombre entré au départ, il s'agit donc ici d'un algorithme qui découvre la factorisation du nombre testé N. Il renvoie 2 facteurs pas forcément premiers.

Il a été signalé qu'un nombre de la forme 2^n renvoie 1*2^n+1 alors que pour un nombre premier P on renvoie 2*P.
L'explication est la suivante:
Entre 2 nombres triangulaires voisins, Tn et T(n-1), il est facile de montrer que la différence Tn-T(n-1)=n. Donc tout entier est différence au moins 1 fois de 2 nombres triangulaires.
Tout nombre premier P est aussi différence de 2 nombres triangulaires, et mis à part 2, cette différence est impaire. Or tout impair est somme de 2 nombres consécutifs. Or l'algorithme tel qu'il est fait renvoie en premier l'égalité pour laquelle la valeur a (le a ième nombre triangulaire) minimale. Pour un nombre premier P:
T(P+1)/2-T(P-3)/2.

Pour un nombre de la forme 2^n, il n'y a pas de valeur paire pour 2 nombres consécutifs, il faudrait prendre un nombre impair de nombres consécutifs, mais c'est impossible avec que des facteurs pairs dans le nombre.
Si N=2^n, la seule valeur renvoyée sera:
TN-T(N-1)=N.

Comme j'ai écrit tantôt que tout nombre entier était différence de 2 nombres triangulaires, il en est de même pour tout nombre triangulaire.

Sauriez vous trouver à la main cette fois toutes les différences possibles entre 2 nombres triangulaires de T35, par exemple ?