 |
#26 - 19-02-2012 11:44:32
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3839
Ingénnierie géométrique inverse n°1
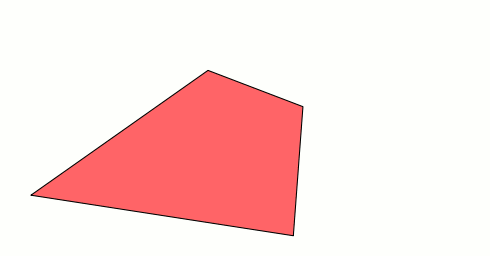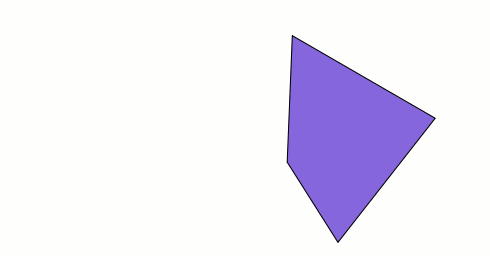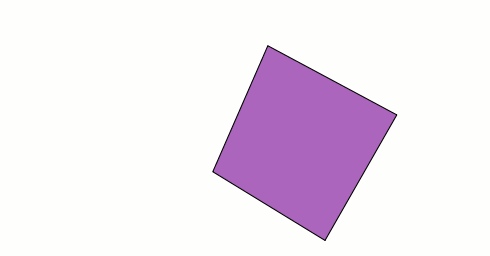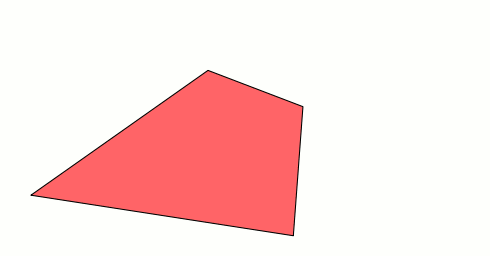
Ces 2 quadrilatères ne représenteraient ils pas, sous des angles différents, la même construction 3D, à savoir 2 triangles non coplanaires soudés par 1 de leurs cotés ?
#27 - 19-02-2012 12:47:55
- looozer
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 697
- Lieu: Belgique
Ingénierie géométriuqe inverse n°1
masab : c'est bien ça! 
nodgim : J'avoue ne pas avoir le courage de chercher comment critiquer ton idée. J'imagine qu'en jouant avec des rotations dans l'espace et la profondeur on doit pouvoir y arriver. La propriété que j'attends est vraie également dans le plan.
#28 - 19-02-2012 13:22:04
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 6,191E+3
Inénierie géométrique inverse n°1
Euh... le milieu des sommets correspondants donnent un carré ?

#29 - 19-02-2012 19:06:18
- looozer
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 697
- Lieu: Belgique
Ingénierie géométriquue inverse n°1
Bonne réponse de gwen27 également!
#30 - 20-02-2012 11:17:54
- masab
- Expert de Prise2Tete
- Enigmes résolues : 44
- Messages : 971
Ingénierie géomtérique inverse n°1
Voici une image illustrant la solution

Visualisation plus complète du morphing en pdf
#31 - 20-02-2012 15:50:20
- looozer
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 697
- Lieu: Belgique
Ingénierie géométique inverse n°1
Merci pour la version décomposée, masab 
#32 - 20-02-2012 18:42:31
- Jackv
- Elite de Prise2Tete
- Enigmes résolues : 34
- Messages : 3609
- Lieu: 94110
Ingénierie géométirque inverse n°1
Ils ont tous les deux 4 cotés ? 
Les couleurs qui les remplissent ont même valeur et même saturation. On passe de l'une à l'autre en inversant les quantités de rouge et de bleu et en gardant la même quantité de vert  ? ?
#33 - 21-02-2012 00:51:20
- looozer
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 697
- Lieu: Belgique
Ingénierie géométrique ivnerse n°1
Merci à tous ceux qui ont cherché sur cette énigme, bravo à ceux qui ont trouvé 
Autant la construction était facile à réaliser en partant du carré, autant le sens inverse était loin de l'évidence.
#34 - 21-02-2012 15:46:18
- masab
- Expert de Prise2Tete
- Enigmes résolues : 44
- Messages : 971
Ingénierie géométrique inverse n°11
Animation du murphing des 2 quadrilatères
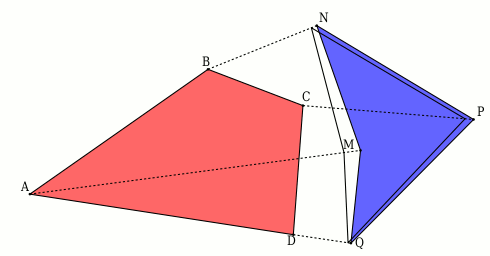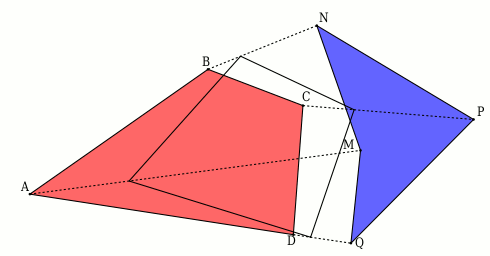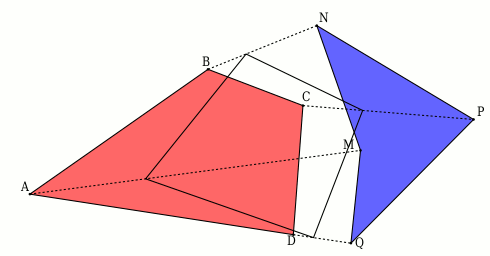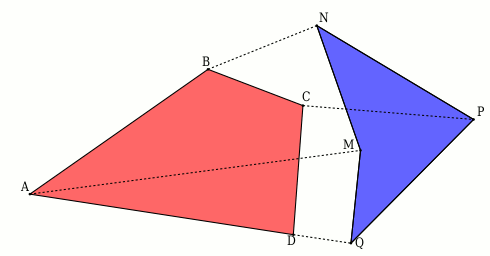
#35 - 21-02-2012 23:13:18
- ksavier
- Professionnel de Prise2Tete
- Enigmes résolues : 49
- Messages : 166
ingénierir géométrique inverse n°1
Je voudrais rassurer tout ceux qui n'ont pas trouvé avant l'indice n°5.  ... oui j'en fait partie !! ... oui j'en fait partie !! 
Je crois que je ne pouvais pas remarquer cette propriété car dans mon esprit elle n'est pas caractéristique. En effet, je pense que si on prend deux quadrilatères quelconques colorés de façon quelconque (en fait n'importe quel couple de figure homéomorphe à un cercle marcherait de la même façon) alors il existe un morphisme continue de [0;1] dans le plan qui envoie le premier sur le second et dont la valeur en 1/2 serait un carré d'une couleur arbitrairement choisie
Voilà, j'avoue, il m'était donc impossible de trouver la réponse. Donc bravo pour la colle.
Belle énigme.
#36 - 22-02-2012 09:36:29
- masab
- Expert de Prise2Tete
- Enigmes résolues : 44
- Messages : 971
Ingénierie géoétrique inverse n°1
Un film du murphing des 2 quadrilatères
#37 - 22-02-2012 11:23:50
- looozer
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 697
- Lieu: Belgique
ingénieeie géométrique inverse n°1
masab : quelle perfectionnisme  ! !
#38 - 22-02-2012 16:42:43
- ksavier
- Professionnel de Prise2Tete
- Enigmes résolues : 49
- Messages : 166
Ingénierie ggéométrique inverse n°1
très belles animations,
J'aurais aimé voir une ou deux animations montrant que ça marchait quels que soient les deux quadrilatères 
#39 - 22-02-2012 18:17:10
- golgot59
- Elite de Prise2Tete
- Enigmes résolues : 48
- Messages : 1494
- Lieu: Coutiches
Ingénieriie géométrique inverse n°1
ksavier, tu es sûr que ça fonctionne quel que soit les deux quadrilatère d'origine ???
En associant un carré avec un quadrilatère quelconque par exemple, je n'ai vraiment pas l'impression que le morphing passe de l'un à l'autre en passant pas un carré...
#40 - 22-02-2012 19:04:36
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
Ingénierie géométrque inverse n°1
Il me semble en effet que le quadrilatère formé par les milieux des deux diagonales des quadrilatères rouge et bleu doit former un parallélogramme pour que le carré médian existe . Dans ce cas le centre du parallélogramme est aussi le centre du carré .
Si les segments reliant les milieux des diagonales ne sont pas de même longueur il n'y a pas de solution . Dans le cas contraire je pense qu'il existe des solutions si on autorise le changement de position relative des deux quadrilatères .
Vasimolo
#41 - 22-02-2012 19:17:14
- golgot59
- Elite de Prise2Tete
- Enigmes résolues : 48
- Messages : 1494
- Lieu: Coutiches
Ingénierie géométrqiue inverse n°1
Tout à fait !
Je pense, pour donner un contre-exemple simple, qu'en reprenant les deux quadrilatères proposés ABCD et MNPQ, mais en rapprochant un peu le point A de B sur [AB], alors les deux quadrilatères obtenus n'ont plus cette jolie propriété...
#42 - 22-02-2012 19:38:12
- ksavier
- Professionnel de Prise2Tete
- Enigmes résolues : 49
- Messages : 166
Ingénierie géoémtrique inverse n°1
golgot59 a écrit:ksavier, tu es sûr que ça fonctionne quel que soit les deux quadrilatère d'origine ???
En associant un carré avec un quadrilatère quelconque par exemple, je n'ai vraiment pas l'impression que le morphing passe de l'un à l'autre en passant pas un carré...
 oui, le carré se déforme en ce que tu veux, puis reforme un carré puis ensuite deviens le second quadrilatère. oui, le carré se déforme en ce que tu veux, puis reforme un carré puis ensuite deviens le second quadrilatère.
En fait, la transformation peut traverser autant de carrés que l'on souhaite.
Mais, ne me faites pas dire ce que je ne dis pas  : je ne dis pas que les sommets au cours de la transformation restent alignés. Je parle d'une transformation inversible ouverte et continue du plan. : je ne dis pas que les sommets au cours de la transformation restent alignés. Je parle d'une transformation inversible ouverte et continue du plan.
Je faisais cette remarque,juste, pour justifier mon incapacité tragiquement honteuse à trouver la réponse de cette énigme, dans laquelle l'existence de la transformation était évidente. En fait, la solution résidait dans la propriété de cette transformation.
#43 - 22-02-2012 19:47:28
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
Ingéniere géométrique inverse n°1
Non ksavier , je crois que tu as tort sauf si tu prends les milieux sur des arcs courbes mais là ça n'a plus d'intérêt 
Vasimolo
#44 - 22-02-2012 20:01:00
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 6,191E+3
ingénierie géométrique incerse n°1
En fait, je suis peut-être simpliste mais si je prends deux quadrilatères quelconques mais identiques , on a une simple translation d'un quadrilatère quelconque.
#45 - 22-02-2012 22:12:21
- SHTF47
- Imprnnçbl de Prs2Tt
- Enigmes résolues : 39
- Messages : 1629
- Lieu: Autre nom du colin
ingébierie géométrique inverse n°1
http://belzel.free .fr/morph2d/adriana2.gif
La musique est une mathématique sonore, la mathématique une musique silencieuse. [Edouard HERRIOT]
#46 - 22-02-2012 22:24:59
- Franky1103
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 3238
- Lieu: Luxembourg
ingénierie géoméyrique inverse n°1
@SHTF47
Ton morphing me laisse un goût ... d'inachevé. 
#47 - 22-02-2012 22:31:51
- ksavier
- Professionnel de Prise2Tete
- Enigmes résolues : 49
- Messages : 166
nIgénierie géométrique inverse n°1
Vasimolo a écrit:Non ksavier , je crois que tu as tort sauf si tu prends les milieux sur des arcs courbes mais là ça n'a plus d'intérêt 
Vasimolo
Je n'ai jamais évoqué un intérêt quelconque. Et comme tout le monde, je ne rejette pas une solution à une énigme sous le seul prétexte qu'elle serait triviale pour l'énigme. 
Aussi, je ne conteste pas la solution proposée
Je dis juste, qu'il est évident que deux quadrilatères quelconques sont homéomorphes, et qu'a partir de là il m'était impossible de partir sur la piste qui consistait à trouver la qualité (alignement des sommets respectifs des 3 quadrilatères) d'une des transformations possibles (une infinité existes) qui envoie le premier quadrilatère sur le second. Et ce, tout simplement car parmi cette infinité de transformations, il doit bien y en avoir ...pfff... à vue de nez (et ne vous moquez pas de mon nez hein !!  ) ...un bon paquet ayant une caractéristique visuelle, géométrique, analytique remarquable. ) ...un bon paquet ayant une caractéristique visuelle, géométrique, analytique remarquable.
#48 - 23-02-2012 11:50:40
- looozer
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 697
- Lieu: Belgique
Ingénierie géommétrique inverse n°1
@SHTF47 : La figure centrale est un carré blanc ?  
Mots clés des moteurs de recherche
|
 |
|
Prise2Tete
Forum
Statistiques
Liste des membres
Hall of Fame
Contact
|

 Accueil
Accueil
 Forum
Forum










