Forum dédié aux énigmes et à toutes formes de jeux de logique. | Déconnexion |
|
Tu n'es pas identifié sur Prise2tete : s'identifier.  Accueil Accueil
 Forum Forum
|
 |
#1 - 14-06-2024 20:40:34
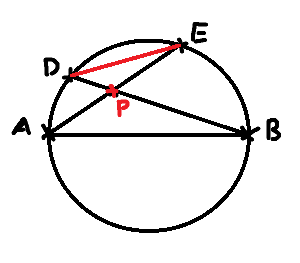
Une construction géométirqueBonsoir!
#0 Pub#2 - 15-06-2024 00:11:15
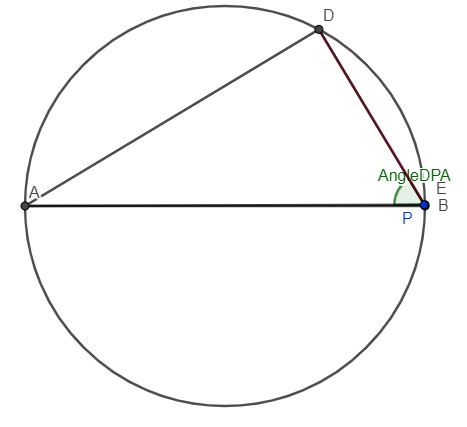
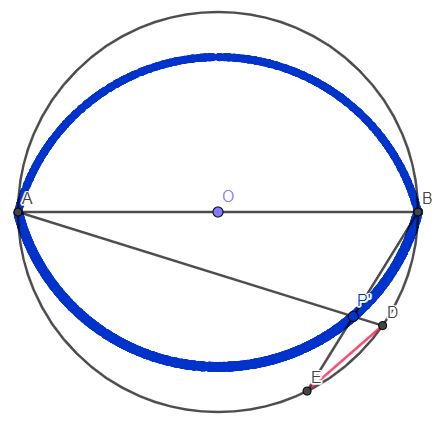
Une construction gométriqueUne position particulière de P qui satisfait à la condition donnée de conservation de la longueur DE. Lélio Lacaille - Du fagot des Nombreux #3 - 15-06-2024 11:39:45#4 - 16-06-2024 20:31:30
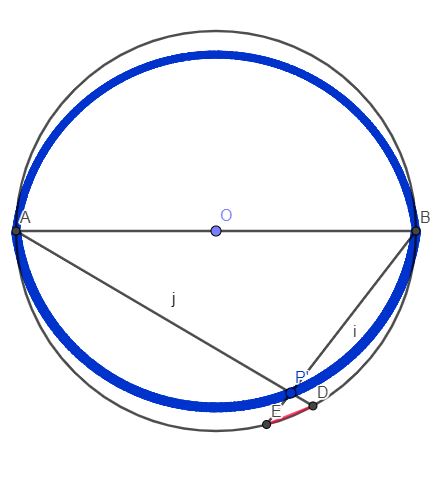
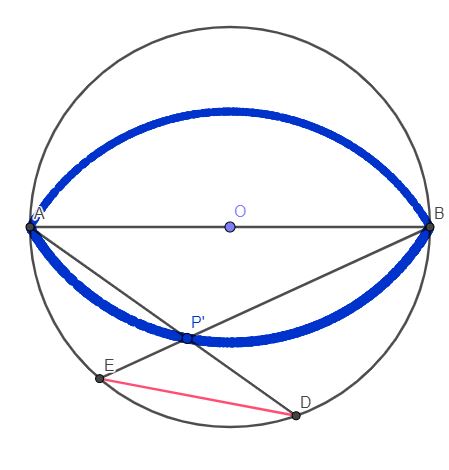
Une construcction géométriqueUne ellipse de demi grand axe R=AB/2 et de demi petit axe R.V(4R²-x²)/(2R+x) #5 - 16-06-2024 21:05:27
ine construction géométrique@aunryz: Ton premier calcul est juste, même si je ne suis pas sûr de comprendre ton raisonnement ^^. Maintenant, il s'agit de décrire les points qui vérifient cette égalité. #6 - 17-06-2024 01:53:37
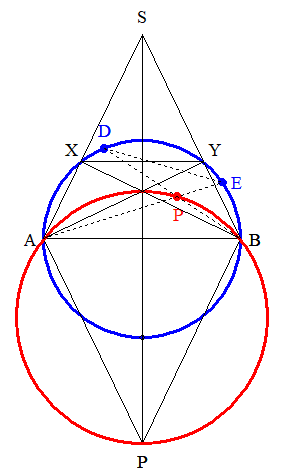
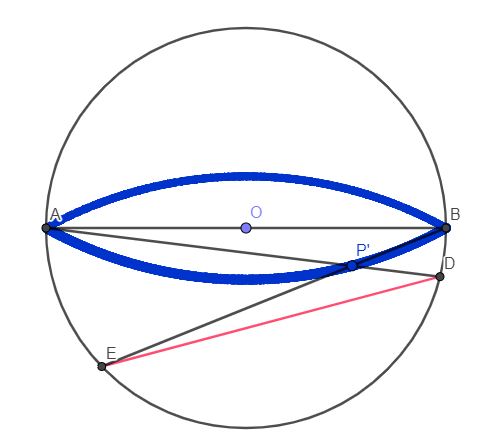
Une construction ggéométriqueDeux arcs de cercle Lélio Lacaille - Du fagot des Nombreux #7 - 17-06-2024 07:09:25#8 - 17-06-2024 12:43:26#9 - 17-06-2024 21:38:25#10 - 22-06-2024 11:12:39
une construction géimétrique#11 - 29-06-2024 16:28:56
une constructuon géométriqueBonjour, Réponse rapideSujets similaires
|
 | |||||||||||||||||||||||||||||||||
| Prise2Tete Forum Statistiques Liste des membres Hall of Fame Contact | |||||||||||||||||||||||||||||||||||
Un jeu où seules la réflexion, la logique et la déduction permettent de trouver la solution.