titoufred a écrit:

Oui, au moment où tu fais ton annonce, tu as bien une chance sur 4 de gagner.
Admettons que l'animateur t'annonce à son tour comment il compte te désigner la moitié du domino tiré au hasard : il te montrera la moitié correspondant au numéro le plus grand.
Peu t'importe, cela ne change rien à ton affaire, tu as toujours une chance sur 4 de gagner.
Maintenant, il procède au tirage au sort du domino. Il regarde le domino et il se trouve qu'il te révèle un 6.
Cette nouvelle information va modifier ta probabilité de gagner, qui va tomber à 1 chance sur 7.

Sûrement pas. Ce n'est parce qu'il annonce un 6 que la proba qu'il ait un double en main est descendue de 1/4 à 1/7. Il n'a pas tiré un 6 parmi les 7 dominos qui comportent un 6, il a tiré un domino parmi 28, dont 7 sont des doubles. J'ai insisté assez lourdement pour être certain des règles du jeu, c'est très important de  connaitre les règles, sinon on ne peut rien conclure.
Ce problème ne s'apparente pas du tout avec l'énigme des 3 portes.

titoufred a écrit:

@Vasimolo : Le problème est posé très clairement, il n'y a que toi qui ne le comprend pas apparemment. Tu ne veux toujours pas tenir compte du fait qu'il ait révélé un 6. Or cette information, bien qu'apparemment sans intérêt, "dissymétrise" le problème et fait qu'il va falloir tenir compte de la stratégie de l'animateur pour évaluer nos chances de gagner quand on répond 6. C'est comme dans le problème avec les chaussettes, tu es obligé de tenir compte de l'information supplémentaire. Puisque tu sais ce qu'est une probabilité conditionnelle, ce qu'il va être important de déterminer c'est entre autres P(66|6) (avec les notations "66" pour "il a tiré le domino 66" et "6" pour "il a montré 6"). Toi tu affirmes que P(66|6)=1/4 quelle que soit la façon dont l'animateur choisit la moitié qu'il révèle. Je te répète que ce n'est pas le cas, cette probabilité dépend de la façon dont l'animateur choisit la moitié qu'il va révéler. On a donné des exemples où cette probabilité vaut 1/7 ou 1. Si tu crois encore et toujours que P(66|6)=1/4, alors vas-y montre-le, tu verras que tu vas bloquer.

Contrairement à ce que tu dis je crois que j'ai parfaitement compris le problème

Voilà comment je le résumerais : l'animateur a mis au point une stratégie pour essayer de faire perdre le candidat . Il tire un domino au hasard , il applique sa stratégie et montre un 6 au candidat . Maintenant quel numéro va choisir le candidat qui voit un 6 et quelle est sa chance de réussite ?

Le candidat choisit 6 et il gagne une fois sur quatre . En quoi l'apparition d'un 6 pourrait faire évoluer la probabilité de réussite dans un sens ou dans l'autre ? Après si la stratégie de l'animateur fait que lorsqu'il montre un 6 les chances de réussite du candidat sont moindre on s'en fout comme de l'an 1000 .

Vasimolo

@Nodgim : La démonstration de Nombrilist est implacable : pour une stratégie donnée de l'animateur, une fois qu'il a montré un 6, la probabilité qu'il ait un double en main est 1/7.

@Vasimolo : Non, l'animateur n'a pas mis au point de stratégie pour faire perdre le candidat plus de 3 fois sur 4. Je répète à l'envi qu'il n'y en a pas. Quelle que soit la façon dont l'animateur choisit la moitié révélée, la stratégie du candidat qui consiste à répondre x quand il voit x assure 1/4 de victoires (voir ce message.) L'animateur a juste sa façon de choisir, dont on ignore tout. Le problème ne consiste pas à montrer qu'il peut faire perdre le candidat plus de 3 fois sur 4. Le problème consiste à montrer que, quelle que soit la façon dont l'animateur a choisi la moitié qu'il a révélée, s'il montre un 6, répondre 6 est le meilleur choix. Ça n'a juste rien à voir.

C'est toi qui tourne en rond... Tu n'es vraiment pas ouvert sur ce coup-là.

Bien sûr qu'il a prise sur les chances de réussite ! Il a prise dans le sens ou il peut les améliorer en dévoilant sa stratégie tu le dis toi-même, te contredisant dans le même post.

S'il dit : je montre une des faces au hasard et qu'il dévoile un 6 , 6 a une chance sur 4 d'être la bonne réponse. Mais le joueur a toujours une chance sur 8 de gagner en répondant 1

S'il dit : je vais faire voir la plus petite des deux faces et qu'il dévoile un 6 , 6 est la bonne réponse et le joueur n'a aucune chance de gagner en répondant 1.

S'il dit : je vais faire voir la plus grande des deux faces et qu'il dévoile un 6 , 6 est une réponse possible et le joueur a autant de chance de gagner en répondant 1 ou 6 : 1/7

Ce que l'on cherche à te faire comprendre est que le 6 , dans tous les cas reste malgré tout la réponse la plus probable. (parfois à égalité)

Nombrilist a écrit:

Titoufred, est-ce que tu pourrais nous donner ta solution avec un raisonnement mathématique, car là, tout le monde raisonne avec son intuition et au final, on n'avance pas.
Pourrais-tu par exemple nous montrer ton raisonnement avec le thérorême de Bayes ? Franchement, ça m'intéresse beaucoup.

Bon, j'ai corrigé mon application du théorême de Bayes. Soient:

P(Double 6 / m6) la probabilité que l'on ait un double 6 sachant que l'animateur montre un 6

P(m6 / Double 6) la probabilité que l'animateur montre un 6 sachant qu'il a un double 6

P(m6) la probabilité que l'animateur montre un 6

P(Double 6) la probabilité qu'il tire un double 6.

Le tirage est aléatoire. Alors:

P(Double 6 / m6) = P(m6 / Double 6) * P(Double 6)/P(m6)

Supposons que le présentateur montre aléatoirement l'une des face. Alors:

P(m6 / Double 6) = 1
P(Double 6) = 1/28
P(m6) = 7/28*8/14 = 1/7

Que représente le 8/14?
P(m6) n'est pas plutôt égal à 7/28 comme montre le dessin

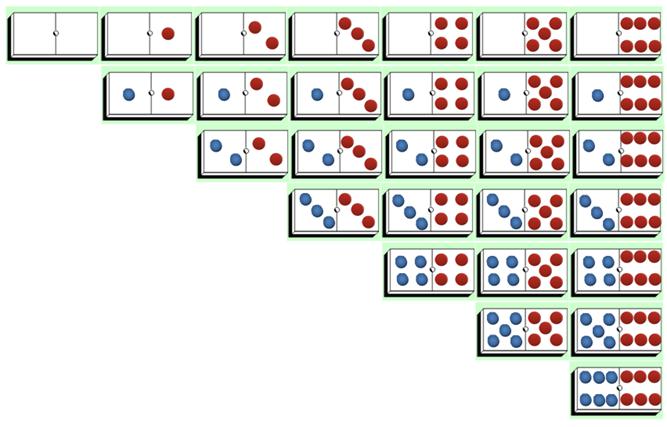
7 dominos,sur les 28, comportent un 6.
Dans ce cas-là,P(Double 6|m6)=1/7.
Donc, le résultat ne dépend PAS de la stratégie de l'animateur.

gwen27 a écrit:

C'est toi qui tourne en rond... Tu n'es vraiment pas ouvert sur ce coup-là.

Bien sûr qu'il a prise sur les chances de réussite ! Il a prise dans le sens ou il peut les améliorer en dévoilant sa stratégie tu le dis toi-même, te contredisant dans le même post.

S'il dit : je montre une des faces au hasard et qu'il dévoile un 6 , 6 a une chance sur 4 d'être la bonne réponse. Mais le joueur a toujours une chance sur 8 de gagner en répondant 1

S'il dit : je vais faire voir la plus petite des deux faces et qu'il dévoile un 6 , 6 est la bonne réponse et le joueur n'a aucune chance de gagner en répondant 1.

S'il dit : je vais faire voir la plus grande des deux faces et qu'il dévoile un 6 , 6 est une réponse possible et le joueur a autant de chance de gagner en répondant 1 ou 6 : 1/7

Ce que l'on cherche à te faire comprendre est que le 6 , dans tous les cas reste malgré tout la réponse la plus probable. (parfois à égalité)

Quand un problème est ambigu au départ on arrive forcément à des discussions sans fin surtout quand le malentendu est entretenu , et je ne suis pas sûr d'être le seul à trouver le problème mal posé . Il n'y a aucune contradiction dans mon message contrairement à ce que tu dis , et se demander s'il y a changement d'espérance  de gain si on voit un 6 est parfaitement ridicule , les différents numéros étant parfaitement interchangeables .

Après il y aurait une autre question qui demanderait si l'animateur pouvait avoir une stratégie ( révélée ) pour laquelle il faudrait choisir une autre solution que 6 .  Évidemment non car même si l'animateur ne décide de montrer un 6 que contraint et forcé , l'autre face a autant de chance d'être un 6 qu'autre chose , il n'y a donc aucun intérêt à choisir autre chose que 6 .

Ce problème vaut-il huit pages

Vasimolo

Nombrilist a écrit:

D'ailleurs, pour conclure sur ce problème, en reprenant mon calcul, on voit bien que pour que l'on n'ait pas moins de 1 chance sur 7 de gagner quelle que soit la stratégie de l'animateur, il faut et il suffit que p(m6)<1/4 (autrement dit, il ne faut pas que l'animateur puisse montrer le 6 plus d'une fois sur 4). Ce qui est évident. CQFD.

Tu viens de montrer que, quelle que soit la façon dont l'animateur choisit la moitié qu'il révèle, la probabilité de gagner en répondant 6 lorsqu'il montre un 6 est supérieure ou égale à 1/7. Cela ne prouve pas pour autant que le 6 reste le meilleur choix.

Vasimolo a écrit:

se demander s'il y a changement d'espérance  de gain si on voit un 6 est parfaitement ridicule , les différents numéros étant parfaitement interchangeables .

Non, dans la façon dont l'animateur choisit la moitié qu'il révèle, les différents numéros ne sont pas forcément interchangeables.

Vasimolo a écrit:

Après il y aurait une autre question qui demanderait si l'animateur pouvait avoir une stratégie ( révélée ) pour laquelle il faudrait choisir une autre solution que 6 .

Ah, enfin, tu as presque compris le problème posé. C'est exactement la question que l'on se pose, sauf que la stratégie de l'animateur n'est pas révélée. Elle nous est inconnue.

Vasimolo a écrit:

Évidemment non car même si l'animateur ne décide de montrer un 6 que contraint et forcé , l'autre face a autant de chance d'être un 6 qu'autre chose , il n'y a donc aucun intérêt à choisir autre chose que 6 .

Tu admets donc enfin que la façon dont l'animateur choisit la moitié qu'il révèle influence notre probabilité de gagner. Bon, ce que tu dis après, c'est juste n'importe quoi.

Soit y un domino contenant un seul 6. On a :

P(y/m6) = p(m6/y)*p(y)/p(m6)

Avec p(m6/y)=<1 suivant la stratégie de l’animateur et  (pm6/y)>0 puisque l’animateur montre un 6.

P(y) = 1/28

Et p(m6) = 7/28 * x avec 1/7=<x=<1

Donc, 0<p(m6/y)/p(m6)=<28/7

Donc p(y/m6)=<1/7

Donc, puisque p(6/m6)>=1/7, la stratégie gagnante est de jouer le 6.

CQFD ?

Edit: il y avait deux erreurs que j'ai corrigées en gras. J'ai écrit p(y/m6) au lieu de p(m6/y). L'encadrement s'obtient en divisant l'encadrement de p(m6/y) par celui de p(m6). Je l'avais mal calculé.

Merci pour la correction. Bon, du coup après correction on trouve p(y/m6)=<1. Nous voilà bien avancé.

Bah, voila, tu as compris... Tu as le droit de trouver le raisonnement ridicule. Ca te gratterait le clavier d'admettre que tu as eu tort ?

Bah non, bien sûr ... Je faisais juste acte de présence pour le plaisir de te faire râler Tout le monde sait que je suis nul à ce genre d'exercice.

A mon avis il faut plus de 2 mn pour le résoudre mais tu restes le seul qui ait mis 10 pages à comprendre la question.  (même si je me suis plutôt positionné dans ton sens au début. )

Ta réponse n'est pas satisfaisante. On ne peut pas juste raisonner en termes d'ensembles comme tu le fais : cela n'explique pas tout ce qu'il y a à expliquer. D'ailleurs, l'animateur n'a pas forcément une stratégie déterminée à l'avance qui stipulerait par exemple "si je tire tel domino alors je montre cette moitié".