 |
#26 - 23-06-2013 21:15:07
- titoufred
- Elite de Prise2Tete
- Enigmes résolues : 20
- Messages : 1749
Longueur du pllus petit morceau
Nombrilist, je ne sais pas s'il y a un raisonnement simple. Chercher P(min(Xi) < x) est intéressant oui.
Je le répète, essaye déjà de chercher le cas n=3 pour comprendre ce qui se passe. Nodgim donne quelques bonnes idées dans son message.
#27 - 24-06-2013 01:45:39
- Gulio
- Amateur de Prise2Tete
- Enigmes résolues : 0
- Messages : 8
Longueru du plus petit morceau
Bonjour,
Pour n=3, je fais le raisonnement suivant: soit x la longueur du plus petit morceau, y la longueur du morceau intermédiaire et z la longueur du plus grand morceau.
x peut varier entre 0 et 1/3
Pour x=0, y peut varier dans l'intervalle [0 ; 0.5] et z dans [0.5 ; 1]
Pour x=0.1, y peut varier dans l'intervalle [0.1 ; 0.45] et z dans [0.45 ; 0.8]
Pour x=0.2, y peut varier dans l'intervalle [0.2 ; 0.4] et z dans [0.4 ; 0.6]
Pour x=0.3, y peut varier dans l'intervalle [0.3 ; 0.35] et z dans [0.35 ; 0.4 ]
...................
On voit par exemple qu'il y a 4 fois plus de chances que x=0.2 que x=0.3, y variant dans un intervalle 4 fois plus grand pour x=0.2 (z étant fixé une fois que x et y fixés)
Pour x quelconque, y varie dans un intervalle de ((1-3x)/2]
J'en déduis la valeur moyenne de x en faisant la moyenne des valeurs prises par x pondérée par la longueur de l'intervalle y.
E[x] = {int[0->1/3] [x(1-3x)]} / {int[0->1/3](1-3x)} = 1/9
(je suis désolé mais je n'ai pas encore latex, je le téléchargerai....)
Pour n quelconque, ça devient vachement compliqué.....Même pour n=4.....c'est trop prise de tête, donc même si on veut démontrer le résultat par récurrence en utilisant les intégrales, c'est chaud.
Est-ce que vous pouvez commenter mon raisonnement ?
#28 - 24-06-2013 11:08:37
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 6,188E+3
Longueur du plus etit morceau
Avec le théorème de Viviani, si on tire un point au hasard dans un triangle de côté 1, la plus petite distance à un côté est la distance moyenne à la base du triangle jaune soit le 1/3 d' 1/3
EDIT , c'est la hauteur qui fait 1, pas le côté !
Ca donne 1/n^2 , non ?
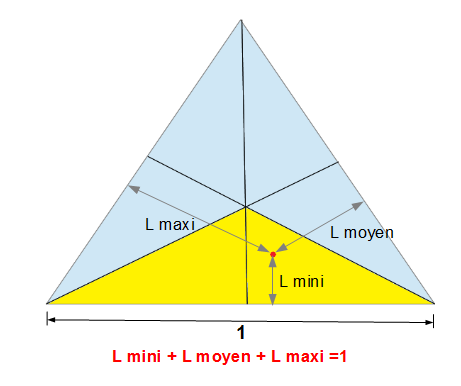
PS : pour le cas n=4, c'est aussi valable dans un tétraèdre régulier de hauteur 1 non ?
Pour le cas n=2 sur un segment de longueur 1
Mais pour le cas n>4, j'ai du mal à imaginer un espace de dimension n-1
#29 - 24-06-2013 14:14:13
- titoufred
- Elite de Prise2Tete
- Enigmes résolues : 20
- Messages : 1749
longueur du plus petit morveau
@Gulio : Bravo pour ta solution. Cependant, le problème est de savoir pourquoi la répartition de (x,y) dans le domaine [0;1/3]x[0;1/2] avec [latex]x \leq y \leq \frac{1-x}{2}[/latex] est uniforme. Je ne doute pas que ce soit le cas, mais il faut expliquer pourquoi.
PS : Pour utiliser Latex, il suffit de cliquer sur l'icône TEX.
@gwen : Bravo pour ta solution. Cependant, tu remplaces un modèle de tirage aléatoire (tirer 2 nombres dans [0;1]) par un autre (tirer un point dans un triangle). Le problème est alors de savoir si ces deux modèles sont équivalents. Je ne doute pas que ce soit le cas, mais il faut expliquer pourquoi.
#30 - 24-06-2013 14:18:58
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 6,188E+3
Lonueur du plus petit morceau
Parce que les conclusions sont liées uniquement au centre des masses du grand triangle dans un premier temps (partage en 3 zones équivalentes) puis du triangle jaune (centre des masses à 1/3 de la hauteur) .
Or le centre des masses par du principe justement, que chaque point a un poids équivalent. (Et on m'excuse si je commets des erreurs de nomenclature SVP)
Aucun point d'une demi zone jaune ne représente le même découpage (je crois)
#31 - 24-06-2013 14:41:39
- titoufred
- Elite de Prise2Tete
- Enigmes résolues : 20
- Messages : 1749
lonfueur du plus petit morceau
Je ne comprends pas très bien ce que tu dis. Je te demande pourquoi la répartition de (Lmini, Lmoyen, Lmaxi) dans ton expérience aléatoire (je tire un point dans un triangle équilatéral de hauteur 1 et je regarde les distances aux bords) est identique à la répartition (Lmini, Lmoyen, Lmaxi) pour l'expérience aléatoire que je donne dans ce problème (je tire deux points dans [0;1] et je regarde les longueurs des morceaux). Ce n'est pas évident que ce soit le cas.
PS : on dit plutôt "centre de gravité" en Maths.
#32 - 24-06-2013 15:16:27
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 6,188E+3
Longueur du plus petit mrceau
Ben, je ne sais pas, mais ça collait bien ... On retrouve la somme à 1, Lmini<1/3 , Lmaxi>1/3, 0<Lmoyen<1/2...
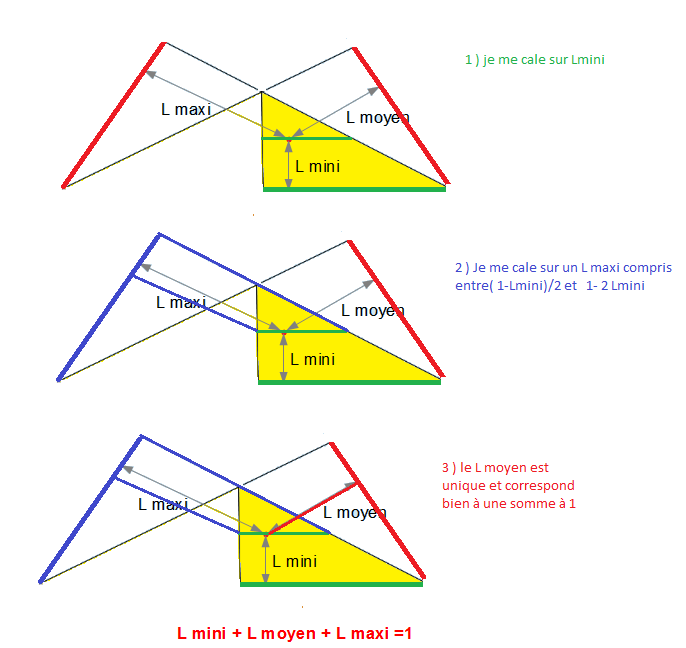
J'ai envie de dire que si les points sont dans l'ordre du plus petit au plus grand, je peux réorganiser le tirage en disant OK j'ai trois longueurs dont le total fait 1.
Est-ce qu'un point de mon demi triangle jaune permet d'avoir ces 3 données ?
Oui.
Et même : un seul.
Et encore mieux : Chaque point peut correspondre à un tirage.
Bon OK, les nombres ont autant de chance d'être dans l'ordre que dans le désordre, mais ça tombe bien, il y a six zones équivalentes dans le triangle équilatéral .
Mais, bon, je suis un peu dépassé par une Preuve possible avec un grand P.
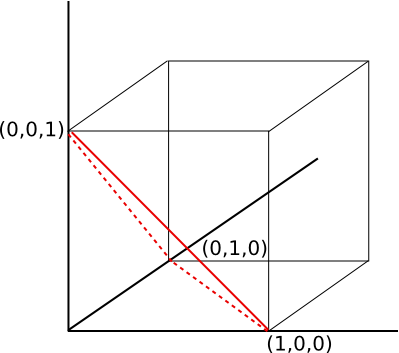
D'ailleurs, x+y+z=1 c'est bien un truc comme ça ?
#33 - 25-06-2013 00:07:20
- titoufred
- Elite de Prise2Tete
- Enigmes résolues : 20
- Messages : 1749
ongueur du plus petit morceau
D'accord gwen, mais il faut prouver que ces 2 expériences aléatoires a priori bien différentes donnent les mêmes lois de probabilité pour Lmini. Ce qui n'est pas évident. Je crois bien que c'est vrai mais il faut voir pourquoi.
Avoir les mêmes intervalles ne suffit pas. Par exemple, si X est une v.a. ayant une loi de proba uniforme sur [0;1], alors X² est une v.a. dans [0;1] mais qui ne suit pas la même loi.
#34 - 25-06-2013 00:09:16
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 6,188E+3
Longueur ddu plus petit morceau
Une bijection ne suffit pas à le prouver ?
#35 - 25-06-2013 00:12:16
- titoufred
- Elite de Prise2Tete
- Enigmes résolues : 20
- Messages : 1749
Longueur du plus petit morceaau
Regarde mon exemple du dessus. Il y a bijection entre X et X² mais ces 2 v.a. ne suivent pas la même loi.
#36 - 25-06-2013 14:29:16
- titoufred
- Elite de Prise2Tete
- Enigmes résolues : 20
- Messages : 1749
ongueur du plus petit morceau
Un indice sur ma façon de voir :
On note [latex]L_{mini}^n[/latex] la variable aléatoire donnant la longueur du plus petit morceau d'un bâton de longueur 1 cassé en n morceaux.
Le but va être de trouver [latex]P(L_{mini}^3<x)[/latex] pour [latex]x \in [0;1/3][/latex].
Pour cela, on peut raisonner à partir de [latex]L_1^3[/latex] la longueur du premier morceau (correspondant à l'extémité 0 de l'intervalle [0;1]) parmi les 3 morceaux du bâton cassé.
Il va y avoir 2 cas :
1)Soit [latex]L_1^3<x[/latex] et alors c'est bon [latex]L_{mini}^3<x[/latex]
2)Soit [latex]L_1^3\geq x[/latex] et alors il faut regarder ce qui se passe sur les 2 morceaux restants. On est ramené à étudier un [latex]L_{mini}^2[/latex] mais sur un bâton plus petit.
Mots clés des moteurs de recherche
|
 |

 Accueil
Accueil
 Forum
Forum








