|
#1 - 08-08-2013 19:13:18
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
#2 - 09-08-2013 08:01:33
- halloduda
- Professionnel de Prise2Tete
- Enigmes résolues : 24
- Messages : 495
- Lieu: Ardèche
gâtzau 61
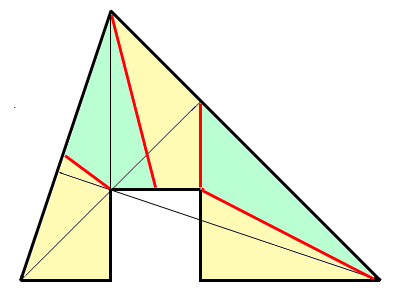
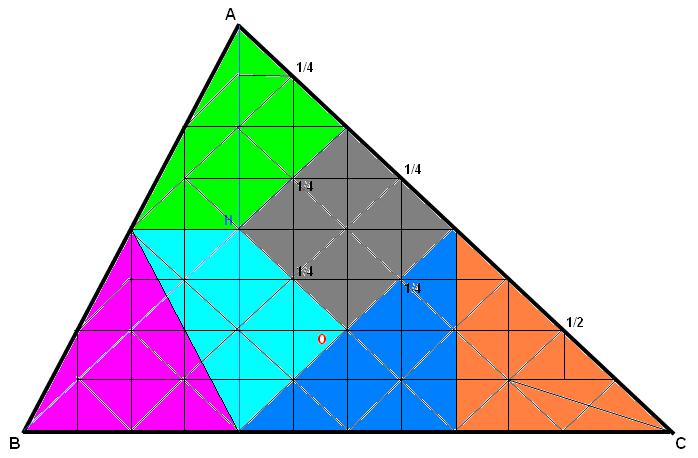
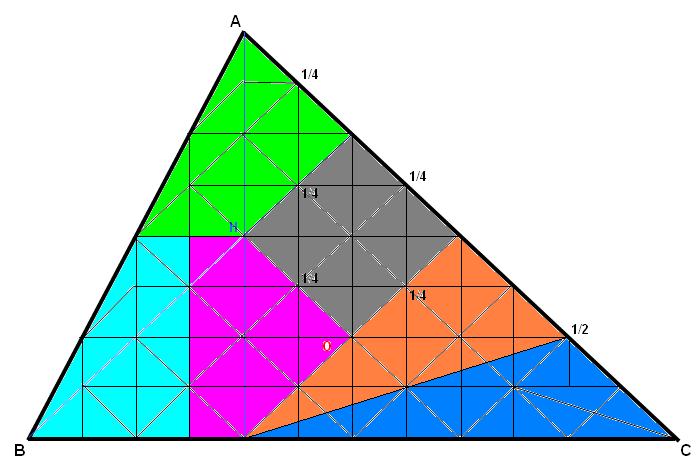
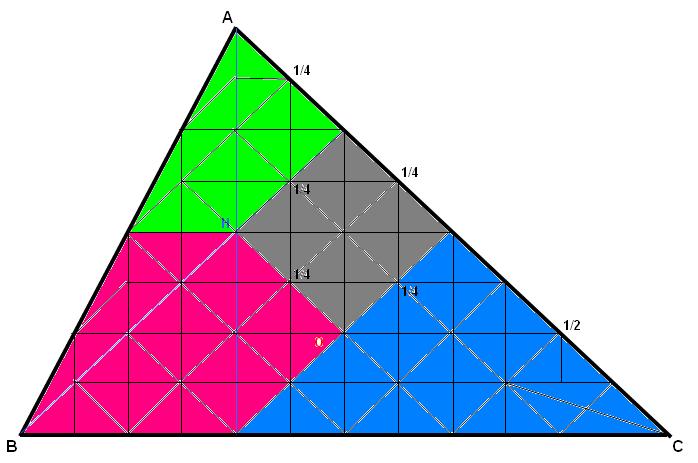
On peut faire 6 parts égales (incluant le cube).
Par exemple :
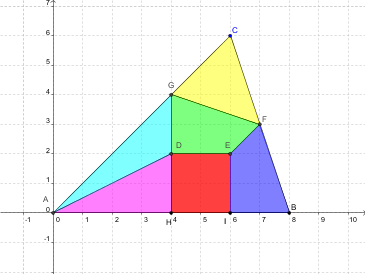
Sur le dessin, tous les sommets ont des coordonnées entières.
EDIT Mes excuses pour les découpes non verticales, ce ne serait pas un problème de modifier.
#3 - 09-08-2013 09:59:47
- fix33
- Elite de Prise2Tete
- Enigmes résolues : 48
- Messages : 1198
- Lieu: Devant un clavier depuis 1748
gâteai 61
Mais est-ce qu'il ne manquerait pas une question ? 
Je ne vien sur se site que pour faire croir que je suis treise intélligens.
#4 - 09-08-2013 12:03:21
- Jackv
- Elite de Prise2Tete
- Enigmes résolues : 34
- Messages : 3614
- Lieu: 94110
#5 - 09-08-2013 12:55:53
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
Gâetau 61
@Halloduda : Nous avons bizarrement le même dessin , est-ce vraiment un hasard ???
@Fix33 : Non , tout est dit mais c'est une énigme  , il faut voir ce qui fait fonctionner le truc . , il faut voir ce qui fait fonctionner le truc .
@Jackv : C'est une autre solution avec le même gâteau ( je n'avais pas prévu ta variante et j'aurais préféré une solution unique  ) )
Vasimolo
#6 - 09-08-2013 13:10:24
- kossi_tg
- Professionnel de Prise2Tete
- Enigmes résolues : 18
- Messages : 307
- Lieu: Montargis
Gââteau 61
Proposition:
Après une étude analytique (que j'ai la flemme de développer ici  ), je suis arrivé aux conclusions suivantes: ), je suis arrivé aux conclusions suivantes:
1-) La droite (OH) est parallèle à la droite (BC) si et seulement si
*** [latex]b\ge\frac{2\sqrt{2}}{3}c[/latex] et
*** l'angle [latex]\hat{c}[/latex] en C est tel que [latex]2cX^2-3bX+c=0 où X=cos(\hat{c})[/latex] ,
2-) La découpe faite par le patissier est cubique si et seulement si [latex]b=\frac{2\sqrt{2}}{3}c[/latex] et dans ce cas [latex]\hat{c}=45°[/latex].
L'aire totale du triangle ABC est égale à [latex]\frac{3b^2}{8}[/latex] et celle de la part découpéé est égale à [latex]\frac{b^2}{16}[/latex]. Le nombre total de parts est donc de 6. Le reste du gateau peut être découpé en 5 parts égales et convexes (Voir la figure ci-dessous).

#7 - 09-08-2013 16:59:39
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
gâyeau 61
Oui Kossi_tg , c'est un nouveau découpage du même gâteau .
Vasimolo
#8 - 10-08-2013 00:02:53
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
Gâteau 611
Une petite précision pour ceux qui sont un peu perdus 
Il y a un seul gâteau correspondant à la part cubique imposée .
Après il y a plusieurs façons de finir le partage mais pas tant que ça .
Vasimolo
#9 - 10-08-2013 10:56:11
- looozer
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 697
- Lieu: Belgique
#10 - 10-08-2013 15:31:29
- golgot59
- Elite de Prise2Tete
- Enigmes résolues : 48
- Messages : 1494
- Lieu: Coutiches
Gtâeau 61
Très intéressant !
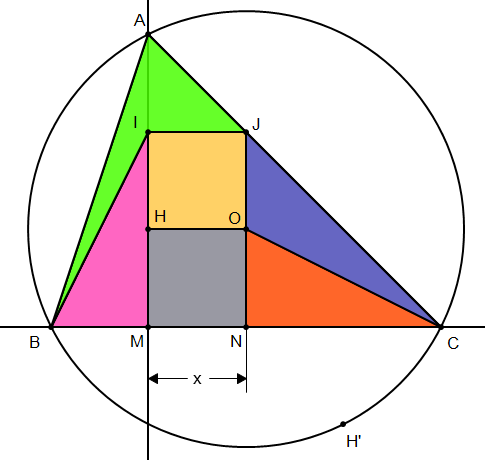
(HO) étant la droite d'Euler, le centre de gravité G se trouve dessus.
Je crée D le pied de la hauteur issue de A et E le point terminant le carré HOED.
Je prends pour repère (B;BC;B...) repère orthonormé, ce qui me donne les coordonnées suivantes :
B(0;0), C(1;0), A(xA;yA), D(xA;0), E(1/2;0) G(xG;yG), H(xA;yG), O(1/2;yG)
(OG) est parallèle à l'axe des abscisses donc le vecteur OG a une ordonnée nulle, on obtient : xG=yA/3
En calculant le produit scalaire DH.EO=0 on trouve :
yA=3.xA-3/2 ou yA=3/2-3.xA
Enfin en calculant BH.AC=0 on trouve : 4xA²-4xA+3/4=0 qui donne :
xA=1/4 ou 3/4 (solution symétrique l'une de l'autre par rapport à la médiatrice de [BC])
La solution est donc unique à cette symétrie près et on obtient : OH = BC/4
Il me reste à découper les 5 parts manquantes (car le carré a une aire 6x plus petite que le gâteau, le calcul se fait facilement maintenant)
#11 - 10-08-2013 17:05:44
- cogito
- Expert de Prise2Tete
- Enigmes résolues : 48
- Messages : 593
Gâtteau 61
Voilà 
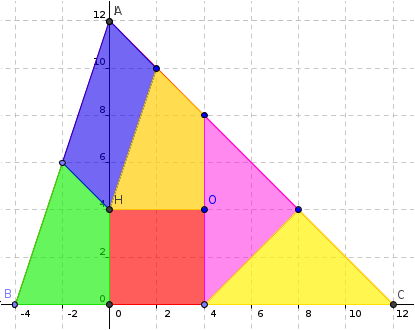
Tentative de justification :
On peut choisir un repère orthonormé et placé 0 et H tels que 0 = (1,1) et H = (0,1).
Comme H est l’orthocentre, alors un des sommet est sur l'axe des ordonnées, appelons A ce point, nous avons donc A = (0,y) pour un certain y. Les deux autres points disons B et C sont sur l'axe des abscisses, donc B = (x,0) et C = (z,0) pour un certain x et un certain z (on supposera x < z).
Comme O est le centre du cercle circonscrit, B et C sont symétriques par rapport à la droite d'équation x = 1. Nous avons donc x - 1 = 1 - z, donc z = 2 - x. Autrement dit C = (2 - x,0).
Note : comme on a supposé x < z alors x < 2 - x et donc x < 1.
Comme O est le centre du cercle circonscrit, on a que OA et OB ont la même norme. On a OA = (-1,y-1) et OB = (x-1,-1), et donc 1 + (y-1)² = (x-1)² + 1,
c'est à dire que (y-1)² = (x-1)² donc y - 1 = x - 1 ou y - 1 = 1 - x, autrement dit
y = x ou y = 2 - x.
Comme H est l'orthocentre, alors BH et AC sont orthogonaux, et donc leur produit scalaire est nul. On a BH = (-x,1) et AC = (2-x,-y), et donc -x(2-x) -y = 0, c'est à dire que y = -x(2-x).
D'après ce qu'on a vu dans les deux paragraphes précédent, on a donc soit
-x(2-x) = x soit -x(2-x) = (2-x). Le premier cas donne x = 0 ou x = 3, x= 0 n'est pas possible et comme x < 1, x = 3 n'est pas possible non plus. Nous sommes donc dans le second cas, et le second cas donne x = 2 ou x = -1 comme x < 1, il reste x = -1. Et donc le seul triangle possible a ses trois sommets aux points de coordonnées (0,3); (-1,0); (3,0).
Après pour la justification du découpage, se reporter au quadrillage  . .
Il y a sûrement plus simple.
#12 - 10-08-2013 19:04:51
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
Gââteau 61
Que du bon avec des méthodes extrêmement variées 
@looozer : y'a un petit défaut de convexité dans la part du haut .
@tous : on peut prouver l'unicité de la solution sans passer par l'analytique .
Vasimolo
#13 - 10-08-2013 19:10:08
- Franky1103
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 3238
- Lieu: Luxembourg
Gâtaeu 61
Je trouve 6 parts, mais avec une solution très "bulldozer" que voici.
Je considère un triangle ONP quelconque dont les sommets ont les coordonnées qui suivent: O(0;0); N(a;b) et P(c;0) et qui a une surface de: S=bc/2.
Equations des médiatrices: x=c/2; y=-(a/b).(x-a/2)+b/2 et y=(c-a).(x-a/2-c/2)+b/2
Coordonnées de l'intersection des médiatrices: M(c/2;(a²+b²-ac)/2b)
Equations des hauteurs: x=a; y=-(a/b).(x-c) et y=(c-a).x/b
Coordonnées de l'intersection des hauteurs: H(a;(ac-a²)/b)
On veut d'abord que: yM=yH, ce qui donne: c=a+b²/3a
d'où: M(a/2+b²/6a;b/3); H(a;b/3) et S=ab/2+b³/6a
Mais on veut aussi que:
1°) Soit xH-xM=yM=yH, ce qui donne: b²+2ab-3a²=0, d'où: b=-3a ou b=a
(b=-3a) est à rejeter car cela donne une surface négative de la part cubique
(b=a) donne une surface de la part cubique de: a²/9, et du triangle de: 2a²/3 et on a donc 6 parts
2°) Soit xM-xH=yM=yH, ce qui donne: b²-2ab-3a²=0, d'où: b=-a ou b=3a
(b=-a) est à rejeter car cela donne une surface négative de la part cubique
(b=3a) donne une surface de la part cubique de: a², et du triangle de: 6a² et on a donc aussi 6 parts
#14 - 10-08-2013 23:54:15
- golgot59
- Elite de Prise2Tete
- Enigmes résolues : 48
- Messages : 1494
- Lieu: Coutiches
Gtâeau 61
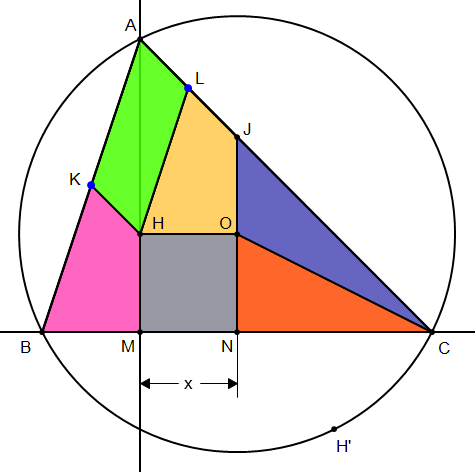
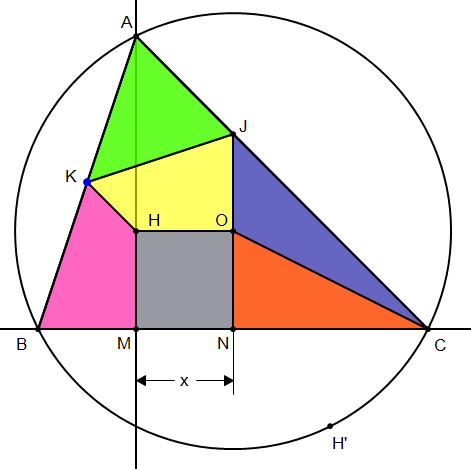
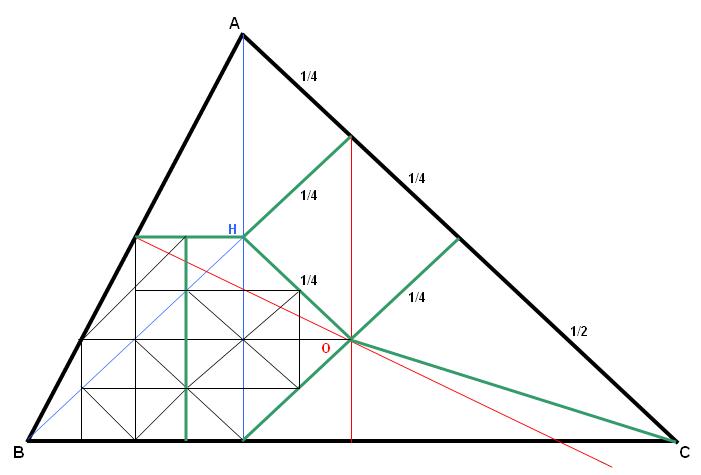
Voici une proposition de découpage : (traits verts)
#15 - 11-08-2013 00:19:43
- golgot59
- Elite de Prise2Tete
- Enigmes résolues : 48
- Messages : 1494
- Lieu: Coutiches
#16 - 11-08-2013 19:27:49
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
#17 - 12-08-2013 12:04:38
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
gâteai 61
Sauf erreur il y avait possibilité de rendre unique la solution à l'énigme en imposant des coupes issues uniquement des points O et H .
Une des solutions proposées par Looozer devient alors la solution .
Je devrais passer un peu plus de temps à peaufiner mes problèmes 
Vasimolo
#18 - 12-08-2013 13:17:29
- godisdead
- Expert de Prise2Tete
- Enigmes résolues : 22
- Messages : 747
âGteau 61
Je ne pense pas, si on regarde le dernier dessin de golgot, la part rouge doit être coupé en deux, elle peut etre découpé à partir de O ou de H !
#19 - 12-08-2013 16:31:02
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
âteau 61
C'est vrai ou alors il faut imposer autant de coupes partant de O que de H mais la consigne devient vraiment pesante 
Vasimolo
Mots clés des moteurs de recherche
|
 |

 Accueil
Accueil
 Forum
Forum