Forum dédié aux énigmes et à toutes formes de jeux de logique. | Déconnexion |
|
Tu n'es pas identifié sur Prise2tete : s'identifier.  Accueil Accueil
 Forum Forum
|
 |
#1 - 12-09-2010 23:01:57
Gâteau 3Il m'aura fallu du temps mais j'ai réussi à coincer mon tourmenteur
#0 Pub#2 - 13-09-2010 00:06:03
Gâeau 33J'ai fait une serie de calcul et obtient 20\sqrt{11} pour le diametre. Y'a qu'un p'tit probleme : le cercle inscrit n'est pas tangent au 4 cotes...oups The proof of the pudding is in the eating. #3 - 13-09-2010 06:40:26#4 - 13-09-2010 22:47:38
gâtrau 33J'ai ajouté un indice qui correspond à la méthode que j'ai utilisée pour determiner le diamètre . #5 - 13-09-2010 23:26:48#6 - 13-09-2010 23:30:29
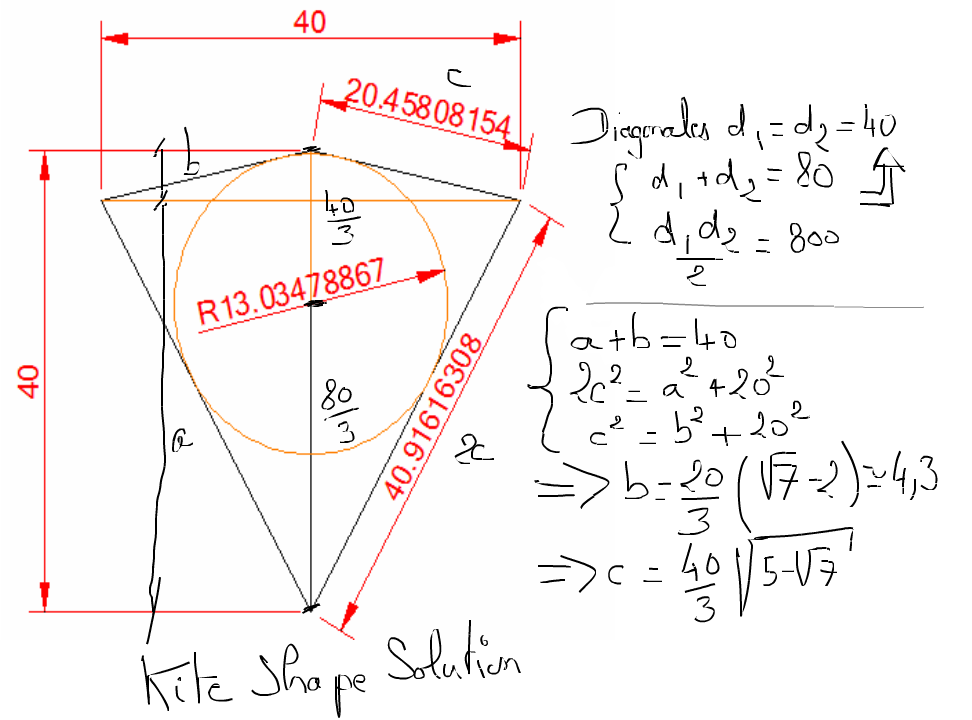
Gâteua 33J'ai finalement trouvé une solution. Cette solution a été trouvée à partir de deux hypothèses: les diagonales sont perpendiculaires et les cotés c et 2c sont adjacents. The proof of the pudding is in the eating. #7 - 14-09-2010 23:46:32#8 - 15-09-2010 00:00:08
Gâteaau 33i agree The proof of the pudding is in the eating. #9 - 16-09-2010 18:31:24#10 - 17-09-2010 17:00:34#11 - 17-09-2010 23:31:18#12 - 18-09-2010 20:14:16#13 - 19-09-2010 07:21:38#14 - 21-09-2010 19:36:40
Gâteau 3Une solution détaillée Réponse rapideSujets similaires
Mots clés des moteurs de recherche |
 | |||||||||||||||||||||||||||||||||
| Prise2Tete Forum Statistiques Liste des membres Hall of Fame Contact | |||||||||||||||||||||||||||||||||||
Un jeu où seules la réflexion, la logique et la déduction permettent de trouver la solution.